Exploiting Structure in Offline Multi-Agent RL: The Benefits of Low Interaction Rank

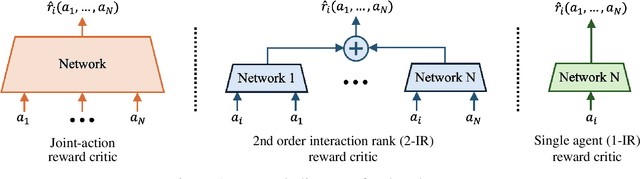
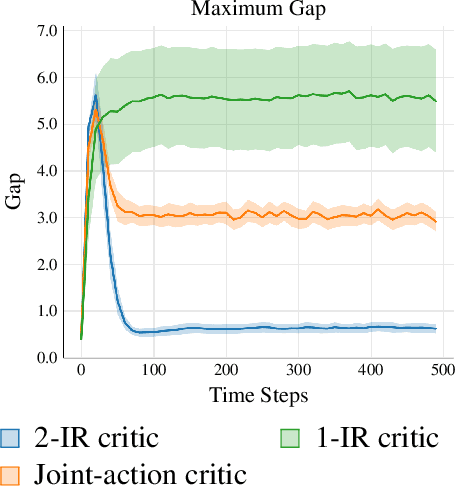
We study the problem of learning an approximate equilibrium in the offline multi-agent reinforcement learning (MARL) setting. We introduce a structural assumption -- the interaction rank -- and establish that functions with low interaction rank are significantly more robust to distribution shift compared to general ones. Leveraging this observation, we demonstrate that utilizing function classes with low interaction rank, when combined with regularization and no-regret learning, admits decentralized, computationally and statistically efficient learning in offline MARL. Our theoretical results are complemented by experiments that showcase the potential of critic architectures with low interaction rank in offline MARL, contrasting with commonly used single-agent value decomposition architectures.

Mathematical Programming For Adaptive Experiments

Adaptive experimentation can significantly improve statistical power, but standard algorithms overlook important practical issues including batched and delayed feedback, personalization, non-stationarity, multiple objectives, and constraints. To address these issues, the current algorithm design paradigm crafts tailored methods for each problem instance. Since it is infeasible to devise novel algorithms for every real-world instance, practitioners often have to resort to suboptimal approximations that do not address all of their challenges. Moving away from developing bespoke algorithms for each setting, we present a mathematical programming view of adaptive experimentation that can flexibly incorporate a wide range of objectives, constraints, and statistical procedures. By formulating a dynamic program in the batched limit, our modeling framework enables the use of scalable optimization methods (e.g., SGD and auto-differentiation) to solve for treatment allocations. We evaluate our framework on benchmarks modeled after practical challenges such as non-stationarity, personalization, multi-objectives, and constraints. Unlike bespoke algorithms such as modified variants of Thomson sampling, our mathematical programming approach provides remarkably robust performance across instances.

AExGym: Benchmarks and Environments for Adaptive Experimentation

Innovations across science and industry are evaluated using randomized trials (a.k.a. A/B tests). While simple and robust, such static designs are inefficient or infeasible for testing many hypotheses. Adaptive designs can greatly improve statistical power in theory, but they have seen limited adoption due to their fragility in practice. We present a benchmark for adaptive experimentation based on real-world datasets, highlighting prominent practical challenges to operationalizing adaptivity: non-stationarity, batched/delayed feedback, multiple outcomes and objectives, and external validity. Our benchmark aims to spur methodological development that puts practical performance (e.g., robustness) as a central concern, rather than mathematical guarantees on contrived instances. We release an open source library, AExGym, which is designed with modularity and extensibility in mind to allow experimentation practitioners to develop custom environments and algorithms.

Weakly Coupled Deep Q-Networks

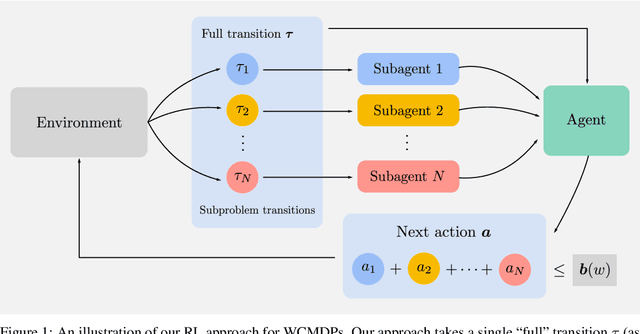
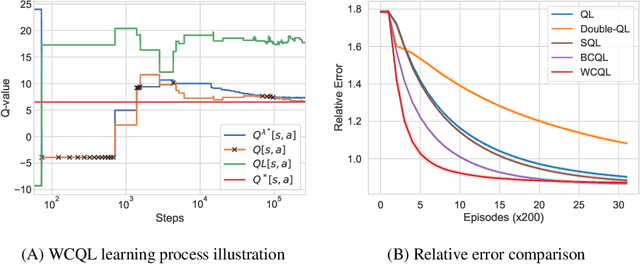
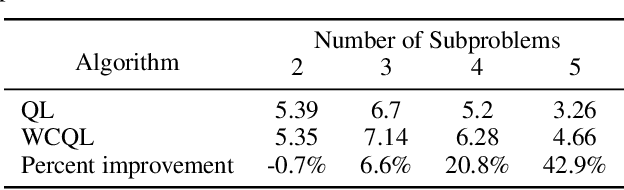
We propose weakly coupled deep Q-networks (WCDQN), a novel deep reinforcement learning algorithm that enhances performance in a class of structured problems called weakly coupled Markov decision processes (WCMDP). WCMDPs consist of multiple independent subproblems connected by an action space constraint, which is a structural property that frequently emerges in practice. Despite this appealing structure, WCMDPs quickly become intractable as the number of subproblems grows. WCDQN employs a single network to train multiple DQN "subagents", one for each subproblem, and then combine their solutions to establish an upper bound on the optimal action value. This guides the main DQN agent towards optimality. We show that the tabular version, weakly coupled Q-learning (WCQL), converges almost surely to the optimal action value. Numerical experiments show faster convergence compared to DQN and related techniques in settings with as many as 10 subproblems, $3^{10}$ total actions, and a continuous state space.

Faster Approximate Dynamic Programming by Freezing Slow States

We consider infinite horizon Markov decision processes (MDPs) with fast-slow structure, meaning that certain parts of the state space move "fast" (and in a sense, are more influential) while other parts transition more "slowly." Such structure is common in real-world problems where sequential decisions need to be made at high frequencies, yet information that varies at a slower timescale also influences the optimal policy. Examples include: (1) service allocation for a multi-class queue with (slowly varying) stochastic costs, (2) a restless multi-armed bandit with an environmental state, and (3) energy demand response, where both day-ahead and real-time prices play a role in the firm's revenue. Models that fully capture these problems often result in MDPs with large state spaces and large effective time horizons (due to frequent decisions), rendering them computationally intractable. We propose an approximate dynamic programming algorithmic framework based on the idea of "freezing" the slow states, solving a set of simpler finite-horizon MDPs (the lower-level MDPs), and applying value iteration (VI) to an auxiliary MDP that transitions on a slower timescale (the upper-level MDP). We also extend the technique to a function approximation setting, where a feature-based linear architecture is used. On the theoretical side, we analyze the regret incurred by each variant of our frozen-state approach. Finally, we give empirical evidence that the frozen-state approach generates effective policies using just a fraction of the computational cost, while illustrating that simply omitting slow states from the decision modeling is often not a viable heuristic.

Multi-Step Budgeted Bayesian Optimization with Unknown Evaluation Costs

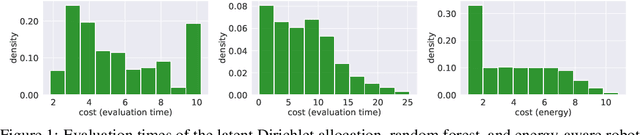
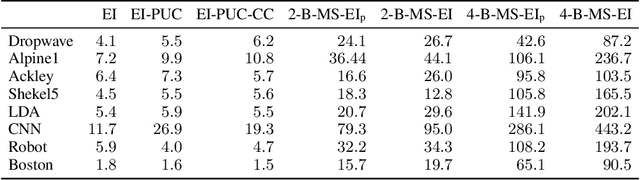
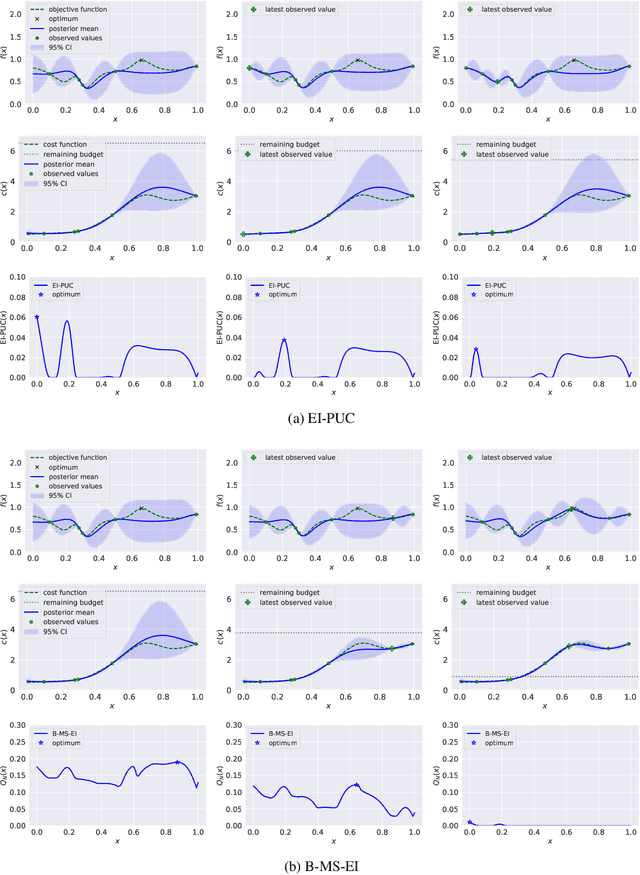
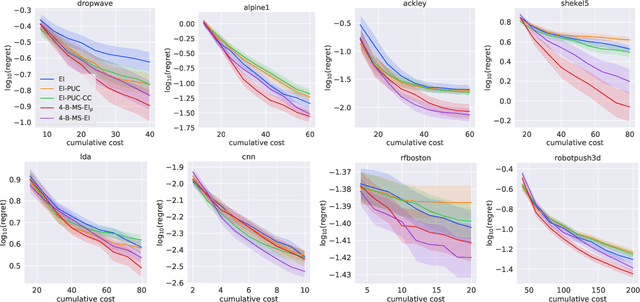
Bayesian optimization (BO) is a sample-efficient approach to optimizing costly-to-evaluate black-box functions. Most BO methods ignore how evaluation costs may vary over the optimization domain. However, these costs can be highly heterogeneous and are often unknown in advance. This occurs in many practical settings, such as hyperparameter tuning of machine learning algorithms or physics-based simulation optimization. Moreover, those few existing methods that acknowledge cost heterogeneity do not naturally accommodate a budget constraint on the total evaluation cost. This combination of unknown costs and a budget constraint introduces a new dimension to the exploration-exploitation trade-off, where learning about the cost incurs the cost itself. Existing methods do not reason about the various trade-offs of this problem in a principled way, leading often to poor performance. We formalize this claim by proving that the expected improvement and the expected improvement per unit of cost, arguably the two most widely used acquisition functions in practice, can be arbitrarily inferior with respect to the optimal non-myopic policy. To overcome the shortcomings of existing approaches, we propose the budgeted multi-step expected improvement, a non-myopic acquisition function that generalizes classical expected improvement to the setting of heterogeneous and unknown evaluation costs. Finally, we show that our acquisition function outperforms existing methods in a variety of synthetic and real problems.

Efficient Nonmyopic Bayesian Optimization via One-Shot Multi-Step Trees

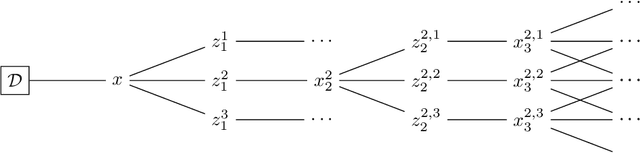
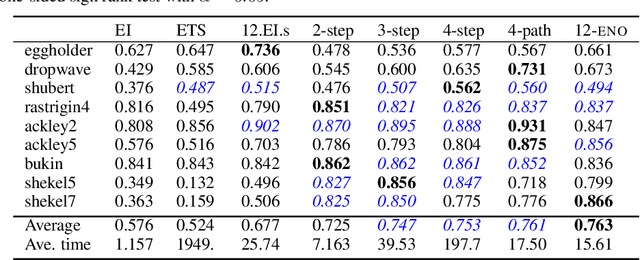
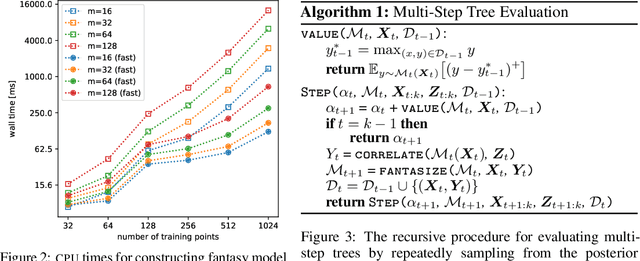
Bayesian optimization is a sequential decision making framework for optimizing expensive-to-evaluate black-box functions. Computing a full lookahead policy amounts to solving a highly intractable stochastic dynamic program. Myopic approaches, such as expected improvement, are often adopted in practice, but they ignore the long-term impact of the immediate decision. Existing nonmyopic approaches are mostly heuristic and/or computationally expensive. In this paper, we provide the first efficient implementation of general multi-step lookahead Bayesian optimization, formulated as a sequence of nested optimization problems within a multi-step scenario tree. Instead of solving these problems in a nested way, we equivalently optimize all decision variables in the full tree jointly, in a ``one-shot'' fashion. Combining this with an efficient method for implementing multi-step Gaussian process ``fantasization,'' we demonstrate that multi-step expected improvement is computationally tractable and exhibits performance superior to existing methods on a wide range of benchmarks.

Lookahead-Bounded Q-Learning

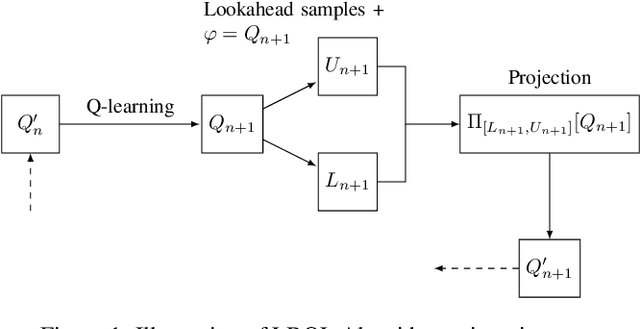
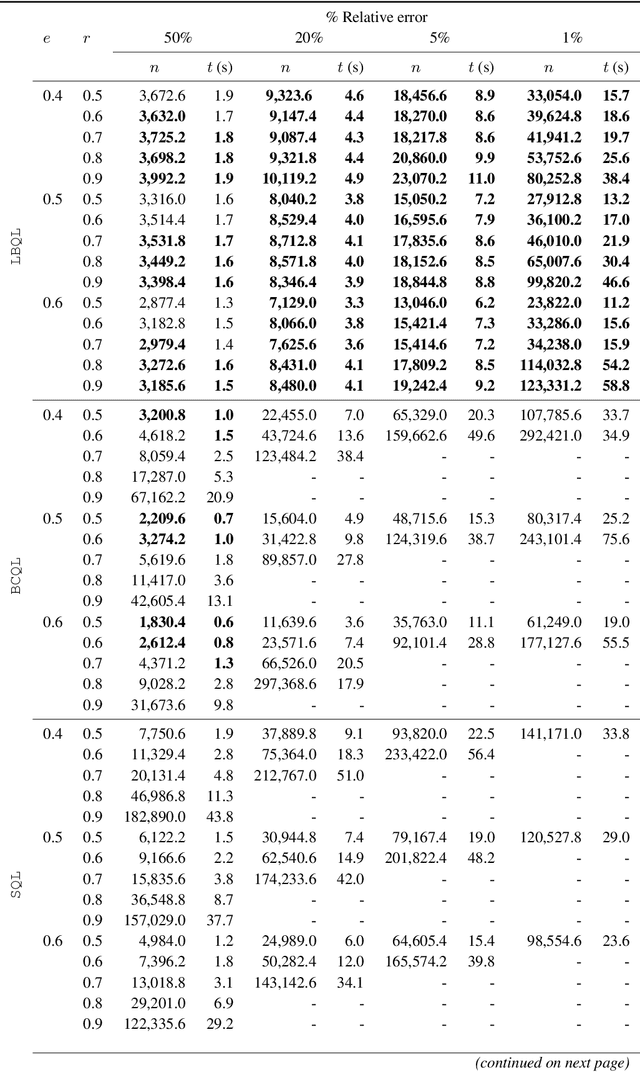
We introduce the lookahead-bounded Q-learning (LBQL) algorithm, a new, provably convergent variant of Q-learning that seeks to improve the performance of standard Q-learning in stochastic environments through the use of ``lookahead'' upper and lower bounds. To do this, LBQL employs previously collected experience and each iteration's state-action values as dual feasible penalties to construct a sequence of sampled information relaxation problems. The solutions to these problems provide estimated upper and lower bounds on the optimal value, which we track via stochastic approximation. These quantities are then used to constrain the iterates to stay within the bounds at every iteration. Numerical experiments on benchmark problems show that LBQL exhibits faster convergence and more robustness to hyperparameters when compared to standard Q-learning and several related techniques. Our approach is particularly appealing in problems that require expensive simulations or real-world interactions.

Exploration via Sample-Efficient Subgoal Design

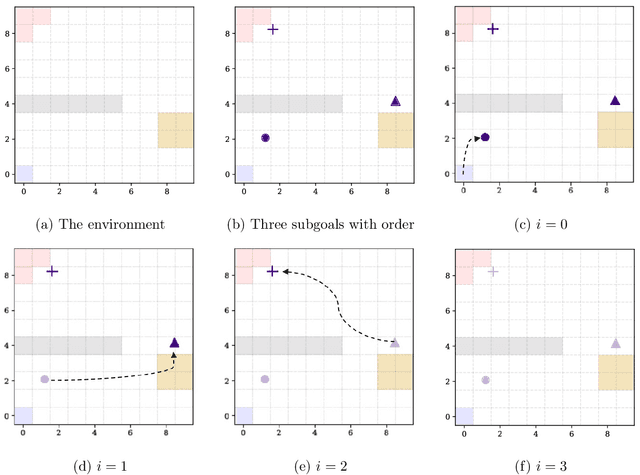
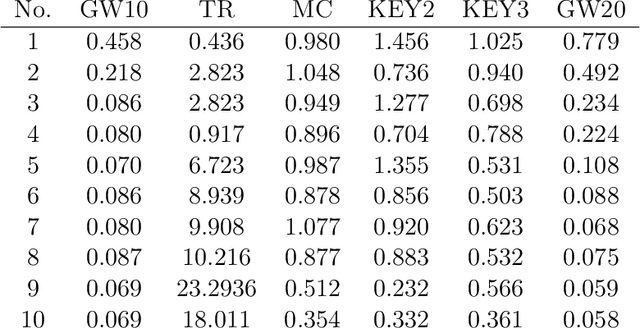
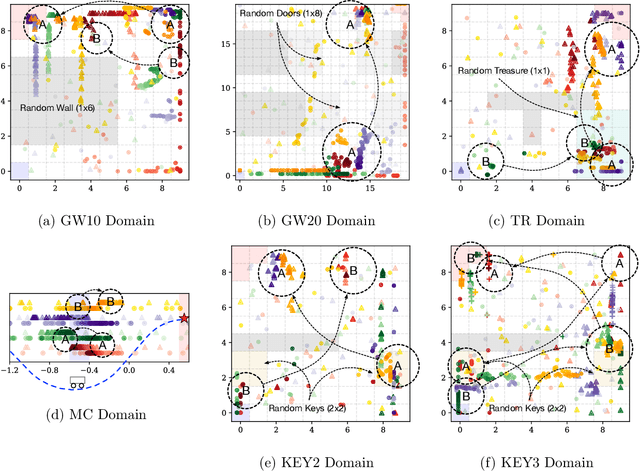
The problem of exploration in unknown environments continues to pose a challenge for reinforcement learning algorithms, as interactions with the environment are usually expensive or limited. The technique of setting subgoals with an intrinsic shaped reward allows for the use of supplemental feedback to aid an agent in environment with sparse and delayed rewards. In fact, it can be an effective tool in directing the exploration behavior of the agent toward useful parts of the state space. In this paper, we consider problems where an agent faces an unknown task in the future and is given prior opportunities to "practice" on related tasks where the interactions are still expensive. We propose a one-step Bayes-optimal algorithm for selecting subgoal designs, along with the number of episodes and the episode length, to efficiently maximize the expected performance of an agent. We demonstrate its excellent performance on a variety of tasks and also prove an asymptotic optimality guarantee.

BoTorch: Programmable Bayesian Optimization in PyTorch

Bayesian optimization provides sample-efficient global optimization for a broad range of applications, including automatic machine learning, molecular chemistry, and experimental design. We introduce BoTorch, a modern programming framework for Bayesian optimization. Enabled by Monte-Carlo (MC) acquisition functions and auto-differentiation, BoTorch's modular design facilitates flexible specification and optimization of probabilistic models written in PyTorch, radically simplifying implementation of novel acquisition functions. Our MC approach is made practical by a distinctive algorithmic foundation that leverages fast predictive distributions and hardware acceleration. In experiments, we demonstrate the improved sample efficiency of BoTorch relative to other popular libraries. BoTorch is open source and available at https://github.com/pytorch/botorch.