Cost-aware Stopping for Bayesian Optimization

In automated machine learning, scientific discovery, and other applications of Bayesian optimization, deciding when to stop evaluating expensive black-box functions is an important practical consideration. While several adaptive stopping rules have been proposed, in the cost-aware setting they lack guarantees ensuring they stop before incurring excessive function evaluation costs. We propose a cost-aware stopping rule for Bayesian optimization that adapts to varying evaluation costs and is free of heuristic tuning. Our rule is grounded in a theoretical connection to state-of-the-art cost-aware acquisition functions, namely the Pandora's Box Gittins Index (PBGI) and log expected improvement per cost. We prove a theoretical guarantee bounding the expected cumulative evaluation cost incurred by our stopping rule when paired with these two acquisition functions. In experiments on synthetic and empirical tasks, including hyperparameter optimization and neural architecture size search, we show that combining our stopping rule with the PBGI acquisition function consistently matches or outperforms other acquisition-function--stopping-rule pairs in terms of cost-adjusted simple regret, a metric capturing trade-offs between solution quality and cumulative evaluation cost.

Fast Bayesian Optimization of Function Networks with Partial Evaluations

Bayesian optimization of function networks (BOFN) is a framework for optimizing expensive-to-evaluate objective functions structured as networks, where some nodes' outputs serve as inputs for others. Many real-world applications, such as manufacturing and drug discovery, involve function networks with additional properties - nodes that can be evaluated independently and incur varying costs. A recent BOFN variant, p-KGFN, leverages this structure and enables cost-aware partial evaluations, selectively querying only a subset of nodes at each iteration. p-KGFN reduces the number of expensive objective function evaluations needed but has a large computational overhead: choosing where to evaluate requires optimizing a nested Monte Carlo-based acquisition function for each node in the network. To address this, we propose an accelerated p-KGFN algorithm that reduces computational overhead with only a modest loss in query efficiency. Key to our approach is generation of node-specific candidate inputs for each node in the network via one inexpensive global Monte Carlo simulation. Numerical experiments show that our method maintains competitive query efficiency while achieving up to a 16x speedup over the original p-KGFN algorithm.

Asymptotically Optimal Regret for Black-Box Predict-then-Optimize

We consider the predict-then-optimize paradigm for decision-making in which a practitioner (1) trains a supervised learning model on historical data of decisions, contexts, and rewards, and then (2) uses the resulting model to make future binary decisions for new contexts by finding the decision that maximizes the model's predicted reward. This approach is common in industry. Past analysis assumes that rewards are observed for all actions for all historical contexts, which is possible only in problems with special structure. Motivated by problems from ads targeting and recommender systems, we study new black-box predict-then-optimize problems that lack this special structure and where we only observe the reward from the action taken. We present a novel loss function, which we call Empirical Soft Regret (ESR), designed to significantly improve reward when used in training compared to classical accuracy-based metrics like mean-squared error. This loss function targets the regret achieved when taking a suboptimal decision; because the regret is generally not differentiable, we propose a differentiable "soft" regret term that allows the use of neural networks and other flexible machine learning models dependent on gradient-based training. In the particular case of paired data, we show theoretically that optimizing our loss function yields asymptotically optimal regret within the class of supervised learning models. We also show our approach significantly outperforms state-of-the-art algorithms on real-world decision-making problems in news recommendation and personalized healthcare compared to benchmark methods from contextual bandits and conditional average treatment effect estimation.

Bayesian Optimization of Function Networks with Partial Evaluations

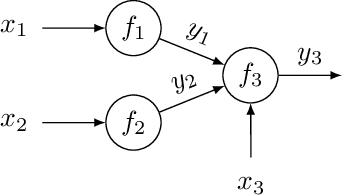
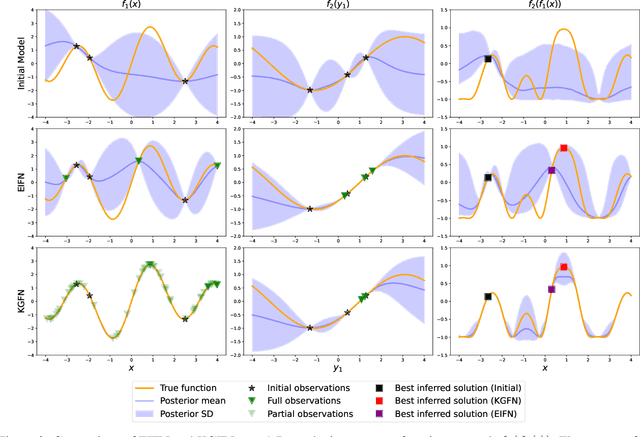
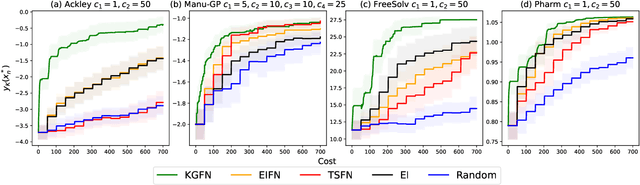
Bayesian optimization is a framework for optimizing functions that are costly or time-consuming to evaluate. Recent work has considered Bayesian optimization of function networks (BOFN), where the objective function is computed via a network of functions, each taking as input the output of previous nodes in the network and additional parameters. Exploiting this network structure has been shown to yield significant performance improvements. Existing BOFN algorithms for general-purpose networks are required to evaluate the full network at each iteration. However, many real-world applications allow evaluating nodes individually. To take advantage of this opportunity, we propose a novel knowledge gradient acquisition function for BOFN that chooses which node to evaluate as well as the inputs for that node in a cost-aware fashion. This approach can dramatically reduce query costs by allowing the evaluation of part of the network at a lower cost relative to evaluating the entire network. We provide an efficient approach to optimizing our acquisition function and show it outperforms existing BOFN methods and other benchmarks across several synthetic and real-world problems. Our acquisition function is the first to enable cost-aware optimization of a broad class of function networks.

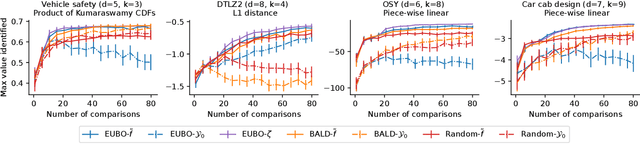
qEUBO: A Decision-Theoretic Acquisition Function for Preferential Bayesian Optimization

Preferential Bayesian optimization (PBO) is a framework for optimizing a decision maker's latent utility function using preference feedback. This work introduces the expected utility of the best option (qEUBO) as a novel acquisition function for PBO. When the decision maker's responses are noise-free, we show that qEUBO is one-step Bayes optimal and thus equivalent to the popular knowledge gradient acquisition function. We also show that qEUBO enjoys an additive constant approximation guarantee to the one-step Bayes-optimal policy when the decision maker's responses are corrupted by noise. We provide an extensive evaluation of qEUBO and demonstrate that it outperforms the state-of-the-art acquisition functions for PBO across many settings. Finally, we show that, under sufficient regularity conditions, qEUBO's Bayesian simple regret converges to zero at a rate $o(1/n)$ as the number of queries, $n$, goes to infinity. In contrast, we show that simple regret under qEI, a popular acquisition function for standard BO often used for PBO, can fail to converge to zero. Enjoying superior performance, simple computation, and a grounded decision-theoretic justification, qEUBO is a promising acquisition function for PBO.

Smooth Non-Stationary Bandits

In many applications of online decision making, the environment is non-stationary and it is therefore crucial to use bandit algorithms that handle changes. Most existing approaches are designed to protect against non-smooth changes, constrained only by total variation or Lipschitzness over time, where they guarantee $T^{2/3}$ regret. However, in practice environments are often changing {\it smoothly}, so such algorithms may incur higher-than-necessary regret in these settings and do not leverage information on the {\it rate of change}. In this paper, we study a non-stationary two-arm bandit problem where we assume an arm's mean reward is a $\beta$-H\"older function over (normalized) time, meaning it is $(\beta-1)$-times Lipschitz-continuously differentiable. We show the first {\it separation} between the smooth and non-smooth regimes by presenting a policy with $T^{3/5}$ regret for $\beta=2$. We complement this result by a $T^{\frac{\beta+1}{2\beta+1}}$ lower bound for any integer $\beta\ge 1$, which matches our upper bound for $\beta=2$.

Regret Bounds and Experimental Design for Estimate-then-Optimize

In practical applications, data is used to make decisions in two steps: estimation and optimization. First, a machine learning model estimates parameters for a structural model relating decisions to outcomes. Second, a decision is chosen to optimize the structural model's predicted outcome as if its parameters were correctly estimated. Due to its flexibility and simple implementation, this ``estimate-then-optimize'' approach is often used for data-driven decision-making. Errors in the estimation step can lead estimate-then-optimize to sub-optimal decisions that result in regret, i.e., a difference in value between the decision made and the best decision available with knowledge of the structural model's parameters. We provide a novel bound on this regret for smooth and unconstrained optimization problems. Using this bound, in settings where estimated parameters are linear transformations of sub-Gaussian random vectors, we provide a general procedure for experimental design to minimize the regret resulting from estimate-then-optimize. We demonstrate our approach on simple examples and a pandemic control application.

Near-optimality for infinite-horizon restless bandits with many arms

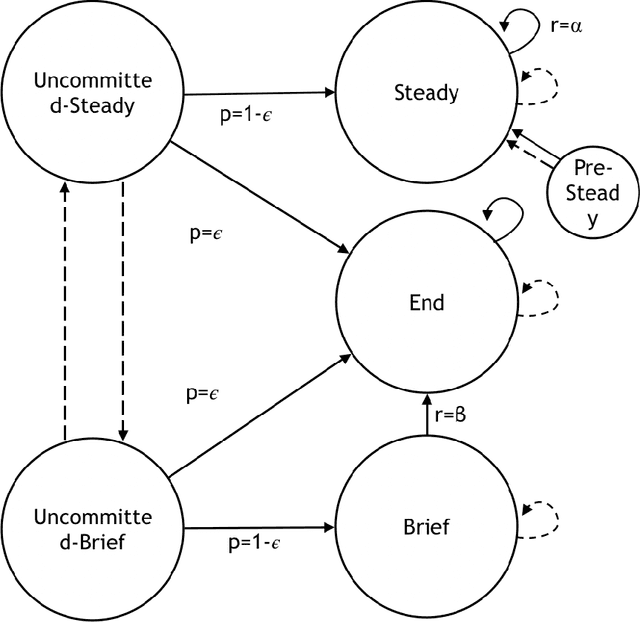
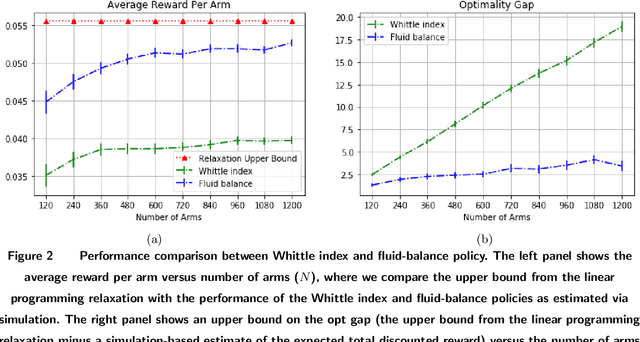
Restless bandits are an important class of problems with applications in recommender systems, active learning, revenue management and other areas. We consider infinite-horizon discounted restless bandits with many arms where a fixed proportion of arms may be pulled in each period and where arms share a finite state space. Although an average-case-optimal policy can be computed via stochastic dynamic programming, the computation required grows exponentially with the number of arms $N$. Thus, it is important to find scalable policies that can be computed efficiently for large $N$ and that are near optimal in this regime, in the sense that the optimality gap (i.e. the loss of expected performance against an optimal policy) per arm vanishes for large $N$. However, the most popular approach, the Whittle index, requires a hard-to-verify indexability condition to be well-defined and another hard-to-verify condition to guarantee a $o(N)$ optimality gap. We present a method resolving these difficulties. By replacing a global Lagrange multiplier used by the Whittle index with a sequence of Lagrangian multipliers, one per time period up to a finite truncation point, we derive a class of policies, called fluid-balance policies, that have a $O(\sqrt{N})$ optimality gap. Unlike the Whittle index, fluid-balance policies do not require indexability to be well-defined and their $O(\sqrt{N})$ optimality gap bound holds universally without sufficient conditions. We also demonstrate empirically that fluid-balance policies provide state-of-the-art performance on specific problems.

Preference Exploration for Efficient Bayesian Optimization with Multiple Outcomes

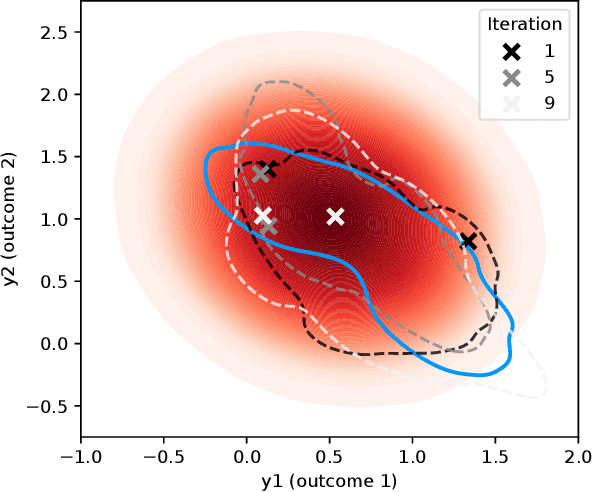
We consider Bayesian optimization of expensive-to-evaluate experiments that generate vector-valued outcomes over which a decision-maker (DM) has preferences. These preferences are encoded by a utility function that is not known in closed form but can be estimated by asking the DM to express preferences over pairs of outcome vectors. To address this problem, we develop Bayesian optimization with preference exploration, a novel framework that alternates between interactive real-time preference learning with the DM via pairwise comparisons between outcomes, and Bayesian optimization with a learned compositional model of DM utility and outcomes. Within this framework, we propose preference exploration strategies specifically designed for this task, and demonstrate their performance via extensive simulation studies.

Thinking inside the box: A tutorial on grey-box Bayesian optimization

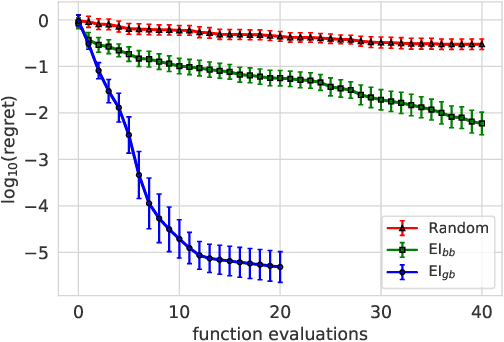
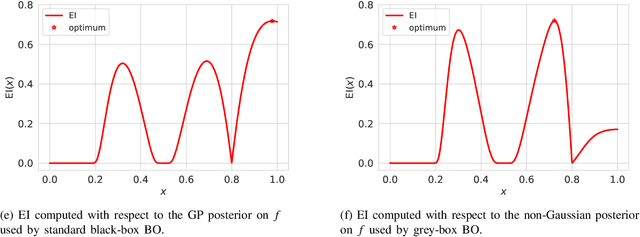
Bayesian optimization (BO) is a framework for global optimization of expensive-to-evaluate objective functions. Classical BO methods assume that the objective function is a black box. However, internal information about objective function computation is often available. For example, when optimizing a manufacturing line's throughput with simulation, we observe the number of parts waiting at each workstation, in addition to the overall throughput. Recent BO methods leverage such internal information to dramatically improve performance. We call these "grey-box" BO methods because they treat objective computation as partially observable and even modifiable, blending the black-box approach with so-called "white-box" first-principles knowledge of objective function computation. This tutorial describes these methods, focusing on BO of composite objective functions, where one can observe and selectively evaluate individual constituents that feed into the overall objective; and multi-fidelity BO, where one can evaluate cheaper approximations of the objective function by varying parameters of the evaluation oracle.