Robust Predictions with Ambiguous Time Delays: A Bootstrap Strategy

In contemporary data-driven environments, the generation and processing of multivariate time series data is an omnipresent challenge, often complicated by time delays between different time series. These delays, originating from a multitude of sources like varying data transmission dynamics, sensor interferences, and environmental changes, introduce significant complexities. Traditional Time Delay Estimation methods, which typically assume a fixed constant time delay, may not fully capture these variabilities, compromising the precision of predictive models in diverse settings. To address this issue, we introduce the Time Series Model Bootstrap (TSMB), a versatile framework designed to handle potentially varying or even nondeterministic time delays in time series modeling. Contrary to traditional approaches that hinge on the assumption of a single, consistent time delay, TSMB adopts a nonparametric stance, acknowledging and incorporating time delay uncertainties. TSMB significantly bolsters the performance of models that are trained and make predictions using this framework, making it highly suitable for a wide range of dynamic and interconnected data environments.

Joint Composite Latent Space Bayesian Optimization

Bayesian Optimization (BO) is a technique for sample-efficient black-box optimization that employs probabilistic models to identify promising input locations for evaluation. When dealing with composite-structured functions, such as f=g o h, evaluating a specific location x yields observations of both the final outcome f(x) = g(h(x)) as well as the intermediate output(s) h(x). Previous research has shown that integrating information from these intermediate outputs can enhance BO performance substantially. However, existing methods struggle if the outputs h(x) are high-dimensional. Many relevant problems fall into this setting, including in the context of generative AI, molecular design, or robotics. To effectively tackle these challenges, we introduce Joint Composite Latent Space Bayesian Optimization (JoCo), a novel framework that jointly trains neural network encoders and probabilistic models to adaptively compress high-dimensional input and output spaces into manageable latent representations. This enables viable BO on these compressed representations, allowing JoCo to outperform other state-of-the-art methods in high-dimensional BO on a wide variety of simulated and real-world problems.

qEUBO: A Decision-Theoretic Acquisition Function for Preferential Bayesian Optimization

Preferential Bayesian optimization (PBO) is a framework for optimizing a decision maker's latent utility function using preference feedback. This work introduces the expected utility of the best option (qEUBO) as a novel acquisition function for PBO. When the decision maker's responses are noise-free, we show that qEUBO is one-step Bayes optimal and thus equivalent to the popular knowledge gradient acquisition function. We also show that qEUBO enjoys an additive constant approximation guarantee to the one-step Bayes-optimal policy when the decision maker's responses are corrupted by noise. We provide an extensive evaluation of qEUBO and demonstrate that it outperforms the state-of-the-art acquisition functions for PBO across many settings. Finally, we show that, under sufficient regularity conditions, qEUBO's Bayesian simple regret converges to zero at a rate $o(1/n)$ as the number of queries, $n$, goes to infinity. In contrast, we show that simple regret under qEI, a popular acquisition function for standard BO often used for PBO, can fail to converge to zero. Enjoying superior performance, simple computation, and a grounded decision-theoretic justification, qEUBO is a promising acquisition function for PBO.

Preference Exploration for Efficient Bayesian Optimization with Multiple Outcomes

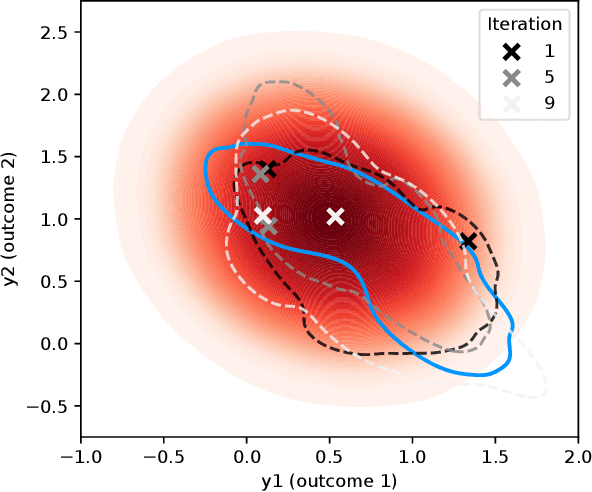
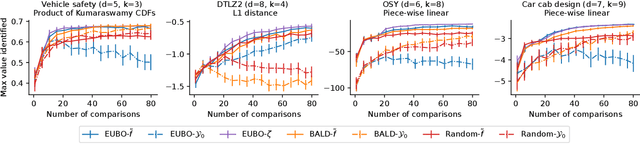
We consider Bayesian optimization of expensive-to-evaluate experiments that generate vector-valued outcomes over which a decision-maker (DM) has preferences. These preferences are encoded by a utility function that is not known in closed form but can be estimated by asking the DM to express preferences over pairs of outcome vectors. To address this problem, we develop Bayesian optimization with preference exploration, a novel framework that alternates between interactive real-time preference learning with the DM via pairwise comparisons between outcomes, and Bayesian optimization with a learned compositional model of DM utility and outcomes. Within this framework, we propose preference exploration strategies specifically designed for this task, and demonstrate their performance via extensive simulation studies.