Covering Multiple Objectives with a Small Set of Solutions Using Bayesian Optimization

In multi-objective black-box optimization, the goal is typically to find solutions that optimize a set of T black-box objective functions, $f_1$, ..., $f_T$, simultaneously. Traditional approaches often seek a single Pareto-optimal set that balances trade-offs among all objectives. In this work, we introduce a novel problem setting that departs from this paradigm: finding a smaller set of K solutions, where K < T, that collectively "covers" the T objectives. A set of solutions is defined as "covering" if, for each objective $f_1$, ..., $f_T$, there is at least one good solution. A motivating example for this problem setting occurs in drug design. For example, we may have T pathogens and aim to identify a set of K < T antibiotics such that at least one antibiotic can be used to treat each pathogen. To address this problem, we propose Multi-Objective Coverage Bayesian Optimization (MOCOBO), a principled algorithm designed to efficiently find a covering set. We validate our approach through extensive experiments on challenging high-dimensional tasks, including applications in peptide and molecular design. Experiments demonstrate MOCOBO's ability to find high-performing covering sets of solutions. Additionally, we show that the small sets of K < T solutions found by MOCOBO can match or nearly match the performance of T individually optimized solutions for the same objectives. Our results highlight MOCOBO's potential to tackle complex multi-objective problems in domains where finding at least one high-performing solution for each objective is critical.

Approximation-Aware Bayesian Optimization

High-dimensional Bayesian optimization (BO) tasks such as molecular design often require 10,000 function evaluations before obtaining meaningful results. While methods like sparse variational Gaussian processes (SVGPs) reduce computational requirements in these settings, the underlying approximations result in suboptimal data acquisitions that slow the progress of optimization. In this paper we modify SVGPs to better align with the goals of BO: targeting informed data acquisition rather than global posterior fidelity. Using the framework of utility-calibrated variational inference, we unify GP approximation and data acquisition into a joint optimization problem, thereby ensuring optimal decisions under a limited computational budget. Our approach can be used with any decision-theoretic acquisition function and is compatible with trust region methods like TuRBO. We derive efficient joint objectives for the expected improvement and knowledge gradient acquisition functions in both the standard and batch BO settings. Our approach outperforms standard SVGPs on high-dimensional benchmark tasks in control and molecular design.

Joint Composite Latent Space Bayesian Optimization

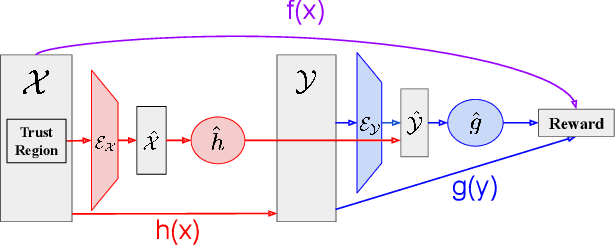
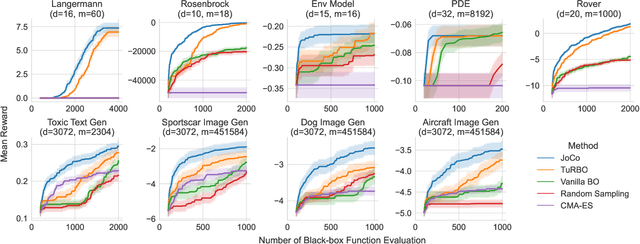
Bayesian Optimization (BO) is a technique for sample-efficient black-box optimization that employs probabilistic models to identify promising input locations for evaluation. When dealing with composite-structured functions, such as f=g o h, evaluating a specific location x yields observations of both the final outcome f(x) = g(h(x)) as well as the intermediate output(s) h(x). Previous research has shown that integrating information from these intermediate outputs can enhance BO performance substantially. However, existing methods struggle if the outputs h(x) are high-dimensional. Many relevant problems fall into this setting, including in the context of generative AI, molecular design, or robotics. To effectively tackle these challenges, we introduce Joint Composite Latent Space Bayesian Optimization (JoCo), a novel framework that jointly trains neural network encoders and probabilistic models to adaptively compress high-dimensional input and output spaces into manageable latent representations. This enables viable BO on these compressed representations, allowing JoCo to outperform other state-of-the-art methods in high-dimensional BO on a wide variety of simulated and real-world problems.

Adversarial Prompting for Black Box Foundation Models

Prompting interfaces allow users to quickly adjust the output of generative models in both vision and language. However, small changes and design choices in the prompt can lead to significant differences in the output. In this work, we develop a black-box framework for generating adversarial prompts for unstructured image and text generation. These prompts, which can be standalone or prepended to benign prompts, induce specific behaviors into the generative process, such as generating images of a particular object or biasing the frequency of specific letters in the generated text.

Local Latent Space Bayesian Optimization over Structured Inputs

Bayesian optimization over the latent spaces of deep autoencoder models (DAEs) has recently emerged as a promising new approach for optimizing challenging black-box functions over structured, discrete, hard-to-enumerate search spaces (e.g., molecules). Here the DAE dramatically simplifies the search space by mapping inputs into a continuous latent space where familiar Bayesian optimization tools can be more readily applied. Despite this simplification, the latent space typically remains high-dimensional. Thus, even with a well-suited latent space, these approaches do not necessarily provide a complete solution, but may rather shift the structured optimization problem to a high-dimensional one. In this paper, we propose LOL-BO, which adapts the notion of trust regions explored in recent work on high-dimensional Bayesian optimization to the structured setting. By reformulating the encoder to function as both an encoder for the DAE globally and as a deep kernel for the surrogate model within a trust region, we better align the notion of local optimization in the latent space with local optimization in the input space. LOL-BO achieves as much as 20 times improvement over state-of-the-art latent space Bayesian optimization methods across six real-world benchmarks, demonstrating that improvement in optimization strategies is as important as developing better DAE models.