Scalable Gaussian Processes with Latent Kronecker Structure

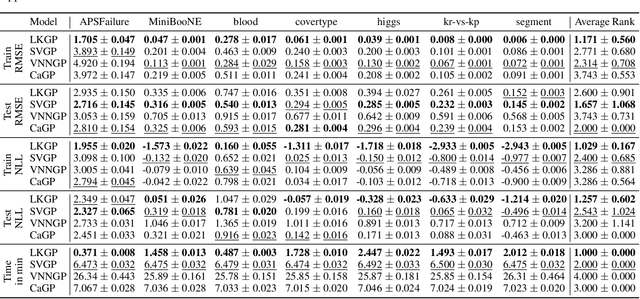
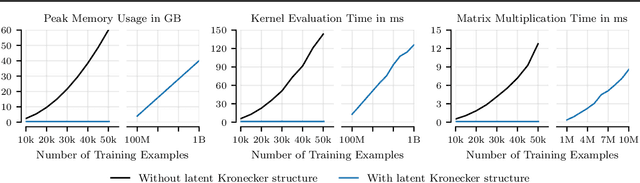
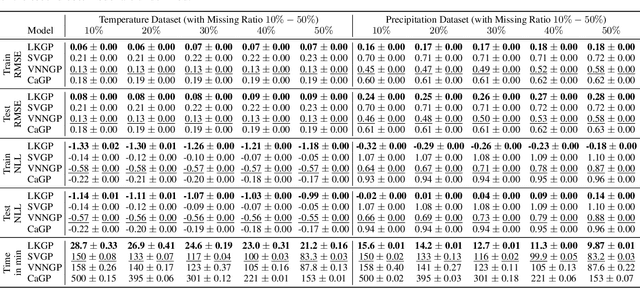
Applying Gaussian processes (GPs) to very large datasets remains a challenge due to limited computational scalability. Matrix structures, such as the Kronecker product, can accelerate operations significantly, but their application commonly entails approximations or unrealistic assumptions. In particular, the most common path to creating a Kronecker-structured kernel matrix is by evaluating a product kernel on gridded inputs that can be expressed as a Cartesian product. However, this structure is lost if any observation is missing, breaking the Cartesian product structure, which frequently occurs in real-world data such as time series. To address this limitation, we propose leveraging latent Kronecker structure, by expressing the kernel matrix of observed values as the projection of a latent Kronecker product. In combination with iterative linear system solvers and pathwise conditioning, our method facilitates inference of exact GPs while requiring substantially fewer computational resources than standard iterative methods. We demonstrate that our method outperforms state-of-the-art sparse and variational GPs on real-world datasets with up to five million examples, including robotics, automated machine learning, and climate applications.

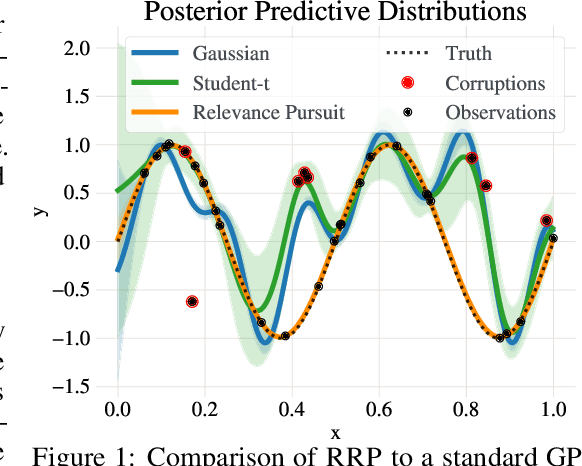
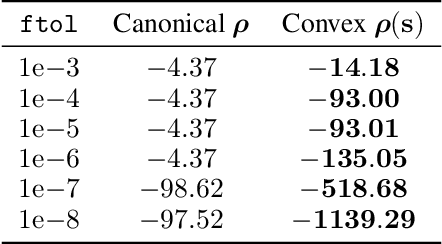
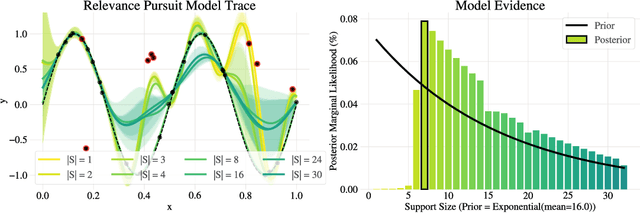
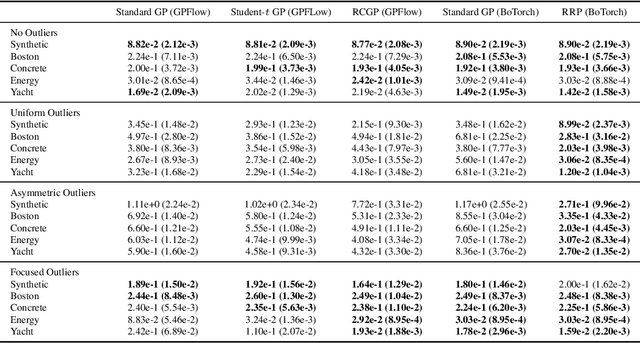
Robust Gaussian Processes via Relevance Pursuit

Gaussian processes (GPs) are non-parametric probabilistic regression models that are popular due to their flexibility, data efficiency, and well-calibrated uncertainty estimates. However, standard GP models assume homoskedastic Gaussian noise, while many real-world applications are subject to non-Gaussian corruptions. Variants of GPs that are more robust to alternative noise models have been proposed, and entail significant trade-offs between accuracy and robustness, and between computational requirements and theoretical guarantees. In this work, we propose and study a GP model that achieves robustness against sparse outliers by inferring data-point-specific noise levels with a sequential selection procedure maximizing the log marginal likelihood that we refer to as relevance pursuit. We show, surprisingly, that the model can be parameterized such that the associated log marginal likelihood is strongly concave in the data-point-specific noise variances, a property rarely found in either robust regression objectives or GP marginal likelihoods. This in turn implies the weak submodularity of the corresponding subset selection problem, and thereby proves approximation guarantees for the proposed algorithm. We compare the model's performance relative to other approaches on diverse regression and Bayesian optimization tasks, including the challenging but common setting of sparse corruptions of the labels within or close to the function range.

Scaling Gaussian Processes for Learning Curve Prediction via Latent Kronecker Structure

A key task in AutoML is to model learning curves of machine learning models jointly as a function of model hyper-parameters and training progression. While Gaussian processes (GPs) are suitable for this task, na\"ive GPs require $\mathcal{O}(n^3m^3)$ time and $\mathcal{O}(n^2 m^2)$ space for $n$ hyper-parameter configurations and $\mathcal{O}(m)$ learning curve observations per hyper-parameter. Efficient inference via Kronecker structure is typically incompatible with early-stopping due to missing learning curve values. We impose $\textit{latent Kronecker structure}$ to leverage efficient product kernels while handling missing values. In particular, we interpret the joint covariance matrix of observed values as the projection of a latent Kronecker product. Combined with iterative linear solvers and structured matrix-vector multiplication, our method only requires $\mathcal{O}(n^3 + m^3)$ time and $\mathcal{O}(n^2 + m^2)$ space. We show that our GP model can match the performance of a Transformer on a learning curve prediction task.

Accelerating Look-ahead in Bayesian Optimization: Multilevel Monte Carlo is All you Need

We leverage multilevel Monte Carlo (MLMC) to improve the performance of multi-step look-ahead Bayesian optimization (BO) methods that involve nested expectations and maximizations. The complexity rate of naive Monte Carlo degrades for nested operations, whereas MLMC is capable of achieving the canonical Monte Carlo convergence rate for this type of problem, independently of dimension and without any smoothness assumptions. Our theoretical study focuses on the approximation improvements for one- and two-step look-ahead acquisition functions, but, as we discuss, the approach is generalizable in various ways, including beyond the context of BO. Findings are verified numerically and the benefits of MLMC for BO are illustrated on several benchmark examples. Code is available here https://github.com/Shangda-Yang/MLMCBO.

Joint Composite Latent Space Bayesian Optimization

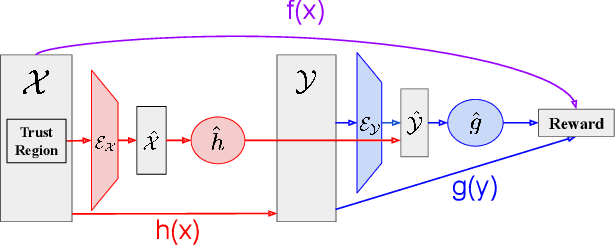
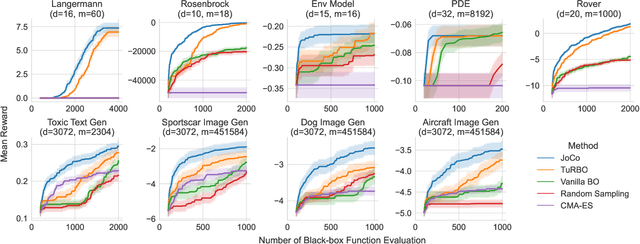
Bayesian Optimization (BO) is a technique for sample-efficient black-box optimization that employs probabilistic models to identify promising input locations for evaluation. When dealing with composite-structured functions, such as f=g o h, evaluating a specific location x yields observations of both the final outcome f(x) = g(h(x)) as well as the intermediate output(s) h(x). Previous research has shown that integrating information from these intermediate outputs can enhance BO performance substantially. However, existing methods struggle if the outputs h(x) are high-dimensional. Many relevant problems fall into this setting, including in the context of generative AI, molecular design, or robotics. To effectively tackle these challenges, we introduce Joint Composite Latent Space Bayesian Optimization (JoCo), a novel framework that jointly trains neural network encoders and probabilistic models to adaptively compress high-dimensional input and output spaces into manageable latent representations. This enables viable BO on these compressed representations, allowing JoCo to outperform other state-of-the-art methods in high-dimensional BO on a wide variety of simulated and real-world problems.

Bayesian Optimization of Function Networks with Partial Evaluations

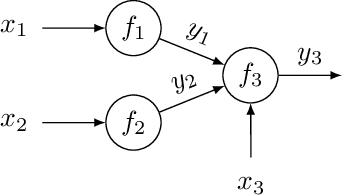
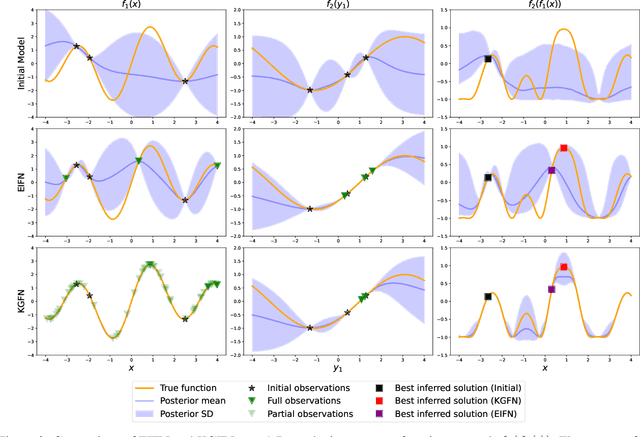
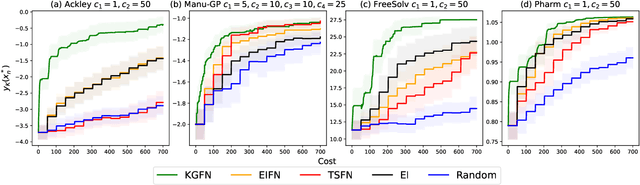
Bayesian optimization is a framework for optimizing functions that are costly or time-consuming to evaluate. Recent work has considered Bayesian optimization of function networks (BOFN), where the objective function is computed via a network of functions, each taking as input the output of previous nodes in the network and additional parameters. Exploiting this network structure has been shown to yield significant performance improvements. Existing BOFN algorithms for general-purpose networks are required to evaluate the full network at each iteration. However, many real-world applications allow evaluating nodes individually. To take advantage of this opportunity, we propose a novel knowledge gradient acquisition function for BOFN that chooses which node to evaluate as well as the inputs for that node in a cost-aware fashion. This approach can dramatically reduce query costs by allowing the evaluation of part of the network at a lower cost relative to evaluating the entire network. We provide an efficient approach to optimizing our acquisition function and show it outperforms existing BOFN methods and other benchmarks across several synthetic and real-world problems. Our acquisition function is the first to enable cost-aware optimization of a broad class of function networks.

Unexpected Improvements to Expected Improvement for Bayesian Optimization

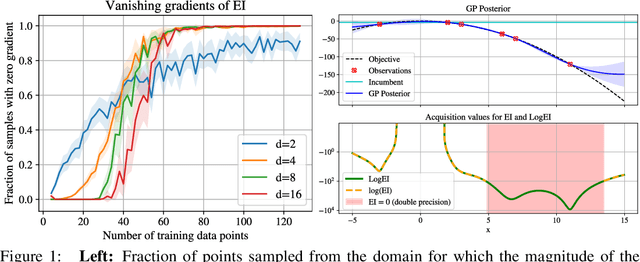
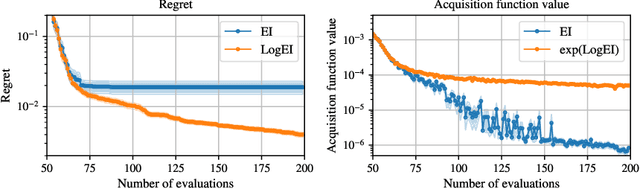
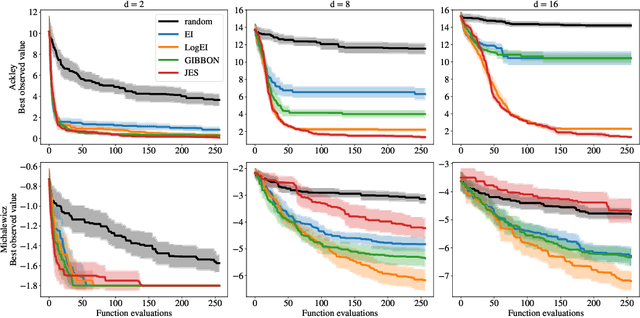
Expected Improvement (EI) is arguably the most popular acquisition function in Bayesian optimization and has found countless successful applications, but its performance is often exceeded by that of more recent methods. Notably, EI and its variants, including for the parallel and multi-objective settings, are challenging to optimize because their acquisition values vanish numerically in many regions. This difficulty generally increases as the number of observations, dimensionality of the search space, or the number of constraints grow, resulting in performance that is inconsistent across the literature and most often sub-optimal. Herein, we propose LogEI, a new family of acquisition functions whose members either have identical or approximately equal optima as their canonical counterparts, but are substantially easier to optimize numerically. We demonstrate that numerical pathologies manifest themselves in "classic" analytic EI, Expected Hypervolume Improvement (EHVI), as well as their constrained, noisy, and parallel variants, and propose corresponding reformulations that remedy these pathologies. Our empirical results show that members of the LogEI family of acquisition functions substantially improve on the optimization performance of their canonical counterparts and surprisingly, are on par with or exceed the performance of recent state-of-the-art acquisition functions, highlighting the understated role of numerical optimization in the literature.

Bayesian Optimization over High-Dimensional Combinatorial Spaces via Dictionary-based Embeddings

We consider the problem of optimizing expensive black-box functions over high-dimensional combinatorial spaces which arises in many science, engineering, and ML applications. We use Bayesian Optimization (BO) and propose a novel surrogate modeling approach for efficiently handling a large number of binary and categorical parameters. The key idea is to select a number of discrete structures from the input space (the dictionary) and use them to define an ordinal embedding for high-dimensional combinatorial structures. This allows us to use existing Gaussian process models for continuous spaces. We develop a principled approach based on binary wavelets to construct dictionaries for binary spaces, and propose a randomized construction method that generalizes to categorical spaces. We provide theoretical justification to support the effectiveness of the dictionary-based embeddings. Our experiments on diverse real-world benchmarks demonstrate the effectiveness of our proposed surrogate modeling approach over state-of-the-art BO methods.

Bayesian Optimization over Discrete and Mixed Spaces via Probabilistic Reparameterization

Optimizing expensive-to-evaluate black-box functions of discrete (and potentially continuous) design parameters is a ubiquitous problem in scientific and engineering applications. Bayesian optimization (BO) is a popular, sample-efficient method that leverages a probabilistic surrogate model and an acquisition function (AF) to select promising designs to evaluate. However, maximizing the AF over mixed or high-cardinality discrete search spaces is challenging standard gradient-based methods cannot be used directly or evaluating the AF at every point in the search space would be computationally prohibitive. To address this issue, we propose using probabilistic reparameterization (PR). Instead of directly optimizing the AF over the search space containing discrete parameters, we instead maximize the expectation of the AF over a probability distribution defined by continuous parameters. We prove that under suitable reparameterizations, the BO policy that maximizes the probabilistic objective is the same as that which maximizes the AF, and therefore, PR enjoys the same regret bounds as the original BO policy using the underlying AF. Moreover, our approach provably converges to a stationary point of the probabilistic objective under gradient ascent using scalable, unbiased estimators of both the probabilistic objective and its gradient. Therefore, as the number of starting points and gradient steps increase, our approach will recover of a maximizer of the AF (an often-neglected requisite for commonly used BO regret bounds). We validate our approach empirically and demonstrate state-of-the-art optimization performance on a wide range of real-world applications. PR is complementary to (and benefits) recent work and naturally generalizes to settings with multiple objectives and black-box constraints.

Robust Multi-Objective Bayesian Optimization Under Input Noise

Bayesian optimization (BO) is a sample-efficient approach for tuning design parameters to optimize expensive-to-evaluate, black-box performance metrics. In many manufacturing processes, the design parameters are subject to random input noise, resulting in a product that is often less performant than expected. Although BO methods have been proposed for optimizing a single objective under input noise, no existing method addresses the practical scenario where there are multiple objectives that are sensitive to input perturbations. In this work, we propose the first multi-objective BO method that is robust to input noise. We formalize our goal as optimizing the multivariate value-at-risk (MVaR), a risk measure of the uncertain objectives. Since directly optimizing MVaR is computationally infeasible in many settings, we propose a scalable, theoretically-grounded approach for optimizing MVaR using random scalarizations. Empirically, we find that our approach significantly outperforms alternative methods and efficiently identifies optimal robust designs that will satisfy specifications across multiple metrics with high probability.