Autonomous Materials Exploration by Integrating Automated Phase Identification and AI-Assisted Human Reasoning

Autonomous experimentation holds the potential to accelerate materials development by combining artificial intelligence (AI) with modular robotic platforms to explore extensive combinatorial chemical and processing spaces. Such self-driving laboratories can not only increase the throughput of repetitive experiments, but also incorporate human domain expertise to drive the search towards user-defined objectives, including improved materials performance metrics. We present an autonomous materials synthesis extension to SARA, the Scientific Autonomous Reasoning Agent, utilizing phase information provided by an automated probabilistic phase labeling algorithm to expedite the search for targeted phase regions. By incorporating human input into an expanded SARA-H (SARA with human-in-the-loop) framework, we enhance the efficiency of the underlying reasoning process. Using synthetic benchmarks, we demonstrate the efficiency of our AI implementation and show that the human input can contribute to significant improvement in sampling efficiency. We conduct experimental active learning campaigns using robotic processing of thin-film samples of several oxide material systems, including Bi$_2$O$_3$, SnO$_x$, and Bi-Ti-O, using lateral-gradient laser spike annealing to synthesize and kinetically trap metastable phases. We showcase the utility of human-in-the-loop autonomous experimentation for the Bi-Ti-O system, where we identify extensive processing domains that stabilize $δ$-Bi$_2$O$_3$ and Bi$_2$Ti$_2$O$_7$, explore dwell-dependent ternary oxide phase behavior, and provide evidence confirming predictions that cationic substitutional doping of TiO$_2$ with Bi inhibits the unfavorable transformation of the metastable anatase to the ground-state rutile phase. The autonomous methods we have developed enable the discovery of new materials and new understanding of materials synthesis and properties.

Scalable Gaussian Processes with Latent Kronecker Structure

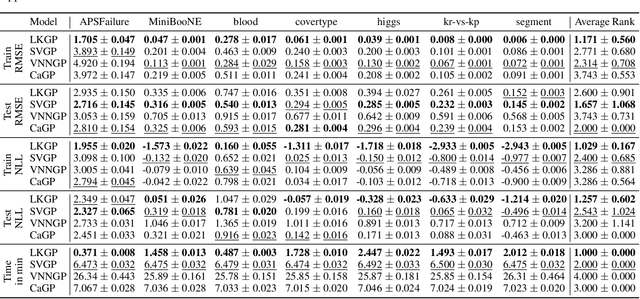
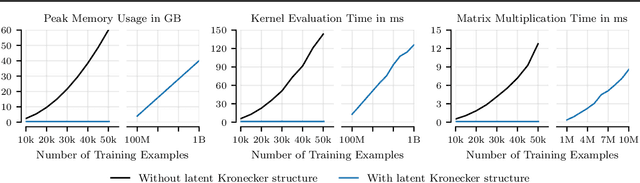
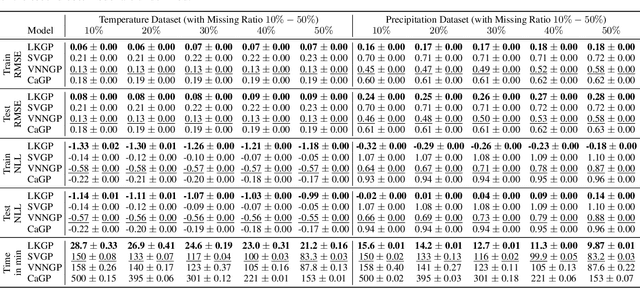
Applying Gaussian processes (GPs) to very large datasets remains a challenge due to limited computational scalability. Matrix structures, such as the Kronecker product, can accelerate operations significantly, but their application commonly entails approximations or unrealistic assumptions. In particular, the most common path to creating a Kronecker-structured kernel matrix is by evaluating a product kernel on gridded inputs that can be expressed as a Cartesian product. However, this structure is lost if any observation is missing, breaking the Cartesian product structure, which frequently occurs in real-world data such as time series. To address this limitation, we propose leveraging latent Kronecker structure, by expressing the kernel matrix of observed values as the projection of a latent Kronecker product. In combination with iterative linear system solvers and pathwise conditioning, our method facilitates inference of exact GPs while requiring substantially fewer computational resources than standard iterative methods. We demonstrate that our method outperforms state-of-the-art sparse and variational GPs on real-world datasets with up to five million examples, including robotics, automated machine learning, and climate applications.

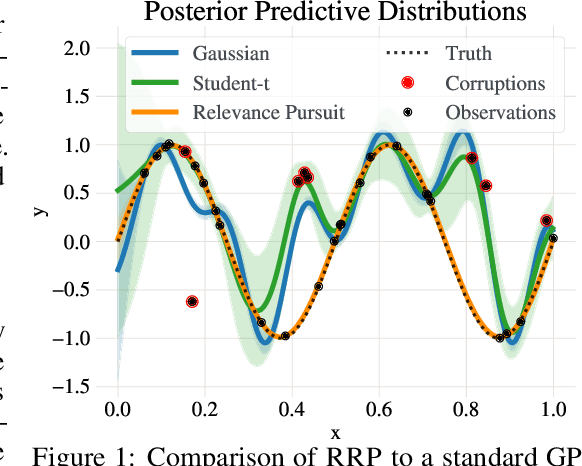
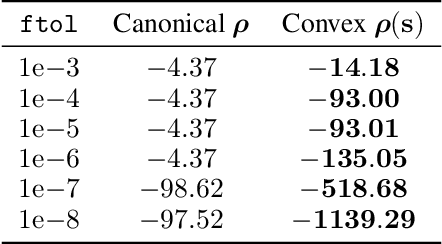
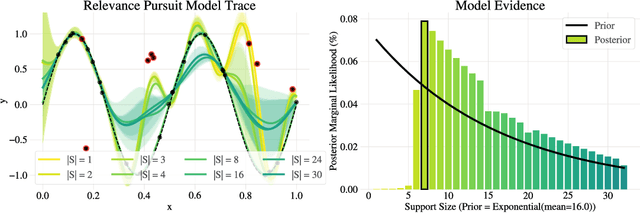
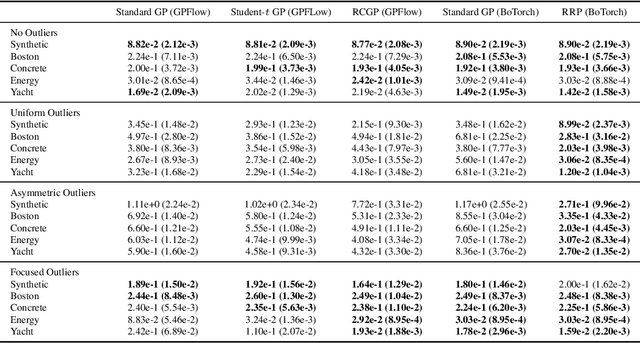
Robust Gaussian Processes via Relevance Pursuit

Gaussian processes (GPs) are non-parametric probabilistic regression models that are popular due to their flexibility, data efficiency, and well-calibrated uncertainty estimates. However, standard GP models assume homoskedastic Gaussian noise, while many real-world applications are subject to non-Gaussian corruptions. Variants of GPs that are more robust to alternative noise models have been proposed, and entail significant trade-offs between accuracy and robustness, and between computational requirements and theoretical guarantees. In this work, we propose and study a GP model that achieves robustness against sparse outliers by inferring data-point-specific noise levels with a sequential selection procedure maximizing the log marginal likelihood that we refer to as relevance pursuit. We show, surprisingly, that the model can be parameterized such that the associated log marginal likelihood is strongly concave in the data-point-specific noise variances, a property rarely found in either robust regression objectives or GP marginal likelihoods. This in turn implies the weak submodularity of the corresponding subset selection problem, and thereby proves approximation guarantees for the proposed algorithm. We compare the model's performance relative to other approaches on diverse regression and Bayesian optimization tasks, including the challenging but common setting of sparse corruptions of the labels within or close to the function range.

Scaling Gaussian Processes for Learning Curve Prediction via Latent Kronecker Structure

A key task in AutoML is to model learning curves of machine learning models jointly as a function of model hyper-parameters and training progression. While Gaussian processes (GPs) are suitable for this task, na\"ive GPs require $\mathcal{O}(n^3m^3)$ time and $\mathcal{O}(n^2 m^2)$ space for $n$ hyper-parameter configurations and $\mathcal{O}(m)$ learning curve observations per hyper-parameter. Efficient inference via Kronecker structure is typically incompatible with early-stopping due to missing learning curve values. We impose $\textit{latent Kronecker structure}$ to leverage efficient product kernels while handling missing values. In particular, we interpret the joint covariance matrix of observed values as the projection of a latent Kronecker product. Combined with iterative linear solvers and structured matrix-vector multiplication, our method only requires $\mathcal{O}(n^3 + m^3)$ time and $\mathcal{O}(n^2 + m^2)$ space. We show that our GP model can match the performance of a Transformer on a learning curve prediction task.

Unexpected Improvements to Expected Improvement for Bayesian Optimization

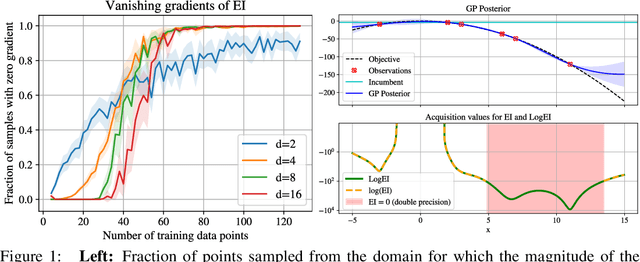
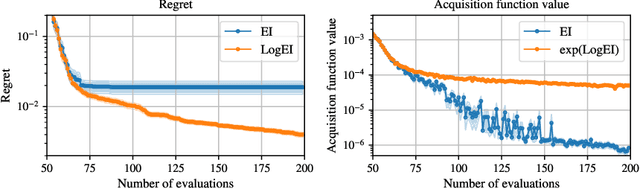
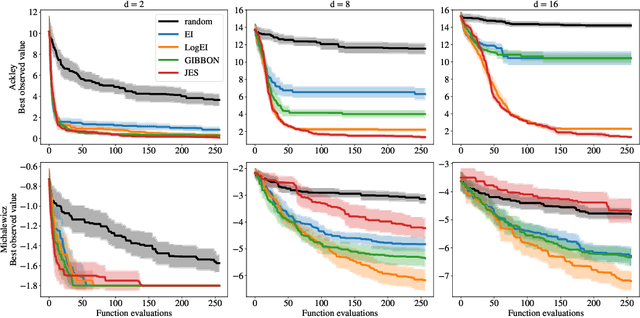
Expected Improvement (EI) is arguably the most popular acquisition function in Bayesian optimization and has found countless successful applications, but its performance is often exceeded by that of more recent methods. Notably, EI and its variants, including for the parallel and multi-objective settings, are challenging to optimize because their acquisition values vanish numerically in many regions. This difficulty generally increases as the number of observations, dimensionality of the search space, or the number of constraints grow, resulting in performance that is inconsistent across the literature and most often sub-optimal. Herein, we propose LogEI, a new family of acquisition functions whose members either have identical or approximately equal optima as their canonical counterparts, but are substantially easier to optimize numerically. We demonstrate that numerical pathologies manifest themselves in "classic" analytic EI, Expected Hypervolume Improvement (EHVI), as well as their constrained, noisy, and parallel variants, and propose corresponding reformulations that remedy these pathologies. Our empirical results show that members of the LogEI family of acquisition functions substantially improve on the optimization performance of their canonical counterparts and surprisingly, are on par with or exceed the performance of recent state-of-the-art acquisition functions, highlighting the understated role of numerical optimization in the literature.

Sustainable Concrete via Bayesian Optimization

Eight percent of global carbon dioxide emissions can be attributed to the production of cement, the main component of concrete, which is also the dominant source of CO2 emissions in the construction of data centers. The discovery of lower-carbon concrete formulae is therefore of high significance for sustainability. However, experimenting with new concrete formulae is time consuming and labor intensive, as one usually has to wait to record the concrete's 28-day compressive strength, a quantity whose measurement can by its definition not be accelerated. This provides an opportunity for experimental design methodology like Bayesian Optimization (BO) to accelerate the search for strong and sustainable concrete formulae. Herein, we 1) propose modeling steps that make concrete strength amenable to be predicted accurately by a Gaussian process model with relatively few measurements, 2) formulate the search for sustainable concrete as a multi-objective optimization problem, and 3) leverage the proposed model to carry out multi-objective BO with real-world strength measurements of the algorithmically proposed mixes. Our experimental results show improved trade-offs between the mixtures' global warming potential (GWP) and their associated compressive strengths, compared to mixes based on current industry practices. Our methods are open-sourced at github.com/facebookresearch/SustainableConcrete.

Probabilistic Phase Labeling and Lattice Refinement for Autonomous Material Research

X-ray diffraction (XRD) is an essential technique to determine a material's crystal structure in high-throughput experimentation, and has recently been incorporated in artificially intelligent agents in autonomous scientific discovery processes. However, rapid, automated and reliable analysis method of XRD data matching the incoming data rate remains a major challenge. To address these issues, we present CrystalShift, an efficient algorithm for probabilistic XRD phase labeling that employs symmetry-constrained pseudo-refinement optimization, best-first tree search, and Bayesian model comparison to estimate probabilities for phase combinations without requiring phase space information or training. We demonstrate that CrystalShift provides robust probability estimates, outperforming existing methods on synthetic and experimental datasets, and can be readily integrated into high-throughput experimental workflows. In addition to efficient phase-mapping, CrystalShift offers quantitative insights into materials' structural parameters, which facilitate both expert evaluation and AI-based modeling of the phase space, ultimately accelerating materials identification and discovery.

Bayesian Optimization over High-Dimensional Combinatorial Spaces via Dictionary-based Embeddings

We consider the problem of optimizing expensive black-box functions over high-dimensional combinatorial spaces which arises in many science, engineering, and ML applications. We use Bayesian Optimization (BO) and propose a novel surrogate modeling approach for efficiently handling a large number of binary and categorical parameters. The key idea is to select a number of discrete structures from the input space (the dictionary) and use them to define an ordinal embedding for high-dimensional combinatorial structures. This allows us to use existing Gaussian process models for continuous spaces. We develop a principled approach based on binary wavelets to construct dictionaries for binary spaces, and propose a randomized construction method that generalizes to categorical spaces. We provide theoretical justification to support the effectiveness of the dictionary-based embeddings. Our experiments on diverse real-world benchmarks demonstrate the effectiveness of our proposed surrogate modeling approach over state-of-the-art BO methods.

Scalable First-Order Bayesian Optimization via Structured Automatic Differentiation

Bayesian Optimization (BO) has shown great promise for the global optimization of functions that are expensive to evaluate, but despite many successes, standard approaches can struggle in high dimensions. To improve the performance of BO, prior work suggested incorporating gradient information into a Gaussian process surrogate of the objective, giving rise to kernel matrices of size $nd \times nd$ for $n$ observations in $d$ dimensions. Na\"ively multiplying with (resp. inverting) these matrices requires $\mathcal{O}(n^2d^2)$ (resp. $\mathcal{O}(n^3d^3$)) operations, which becomes infeasible for moderate dimensions and sample sizes. Here, we observe that a wide range of kernels gives rise to structured matrices, enabling an exact $\mathcal{O}(n^2d)$ matrix-vector multiply for gradient observations and $\mathcal{O}(n^2d^2)$ for Hessian observations. Beyond canonical kernel classes, we derive a programmatic approach to leveraging this type of structure for transformations and combinations of the discussed kernel classes, which constitutes a structure-aware automatic differentiation algorithm. Our methods apply to virtually all canonical kernels and automatically extend to complex kernels, like the neural network, radial basis function network, and spectral mixture kernels without any additional derivations, enabling flexible, problem-dependent modeling while scaling first-order BO to high $d$.

Constrained Machine Learning: The Bagel Framework

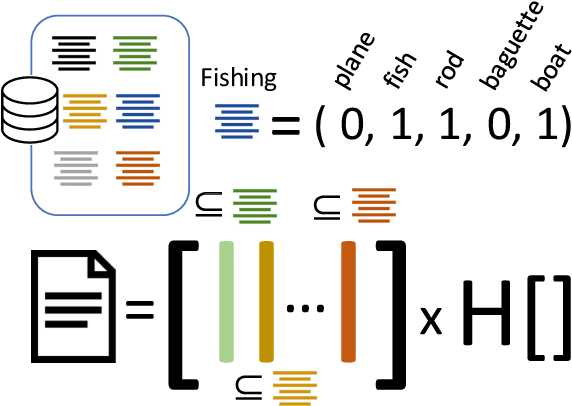
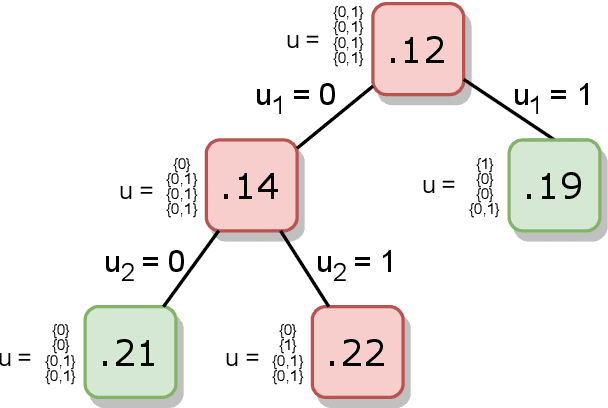
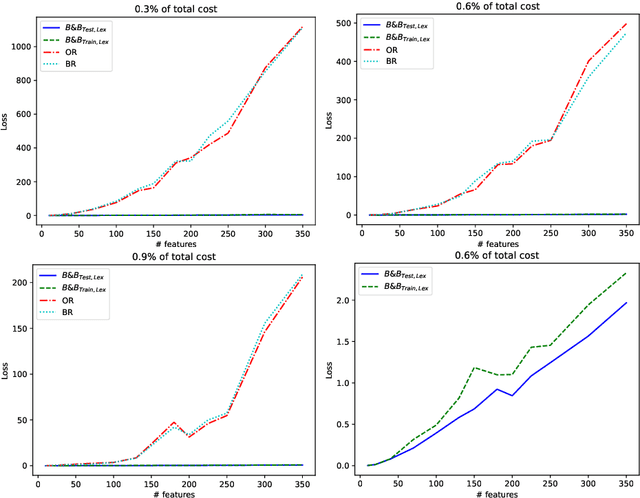
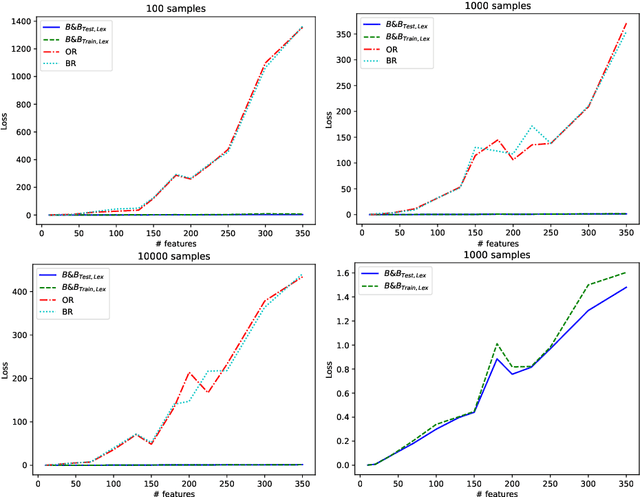
Machine learning models are widely used for real-world applications, such as document analysis and vision. Constrained machine learning problems are problems where learned models have to both be accurate and respect constraints. For continuous convex constraints, many works have been proposed, but learning under combinatorial constraints is still a hard problem. The goal of this paper is to broaden the modeling capacity of constrained machine learning problems by incorporating existing work from combinatorial optimization. We propose first a general framework called BaGeL (Branch, Generate and Learn) which applies Branch and Bound to constrained learning problems where a learning problem is generated and trained at each node until only valid models are obtained. Because machine learning has specific requirements, we also propose an extended table constraint to split the space of hypotheses. We validate the approach on two examples: a linear regression under configuration constraints and a non-negative matrix factorization with prior knowledge for latent semantics analysis.