A Constraint Programming Model for Scheduling the Unloading of Trains in Ports: Extended

In this paper, we propose a model to schedule the next 24 hours of operations in a bulk cargo port to unload bulk cargo trains onto stockpiles. It is a problem that includes multiple parts such as splitting long trains into shorter ones and the routing of bulk material through a configurable network of conveyors to the stockpiles. Managing such trains (up to three kilometers long) also requires specialized equipment. The real world nature of the problem specification implies the necessity to manage heterogeneous data. Indeed, when new equipment is added (e.g. dumpers) or a new type of wagon comes in use, older or different equipment will still be in use as well. All these details need to be accounted for. In fact, avoiding a full deadlock of the facility after a new but ineffective schedule is produced. In this paper, we provide a detailed presentation of this real world problem and its associated data. This allows us to propose an effective constraint programming model to solve this problem. We also discuss the model design and the different implementations of the propagators that we used in practice. Finally, we show how this model, coupled with a large neighborhood search, was able to find 24 hour schedules efficiently.

Constrained Machine Learning: The Bagel Framework

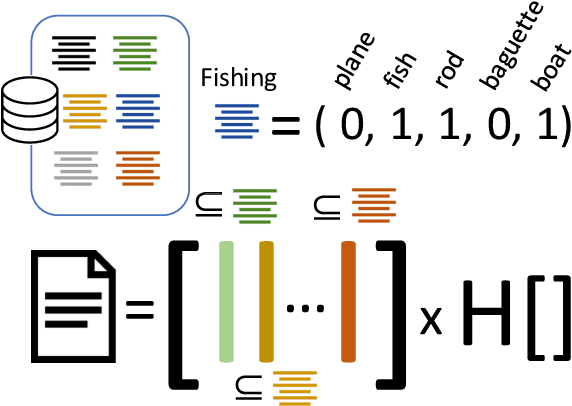
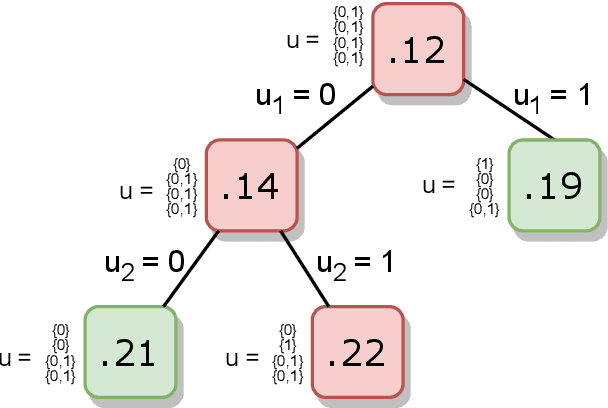
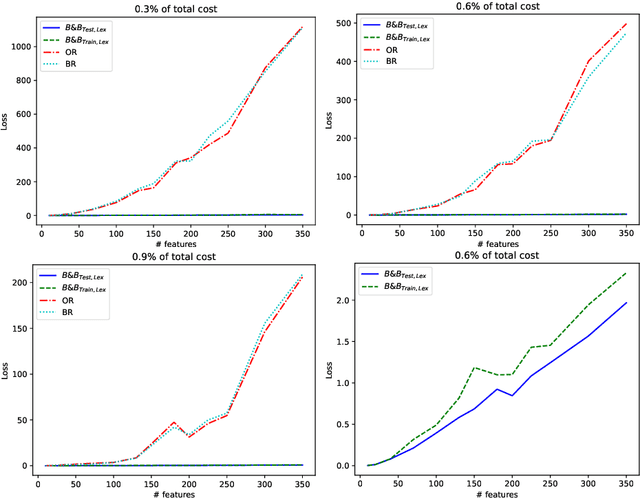
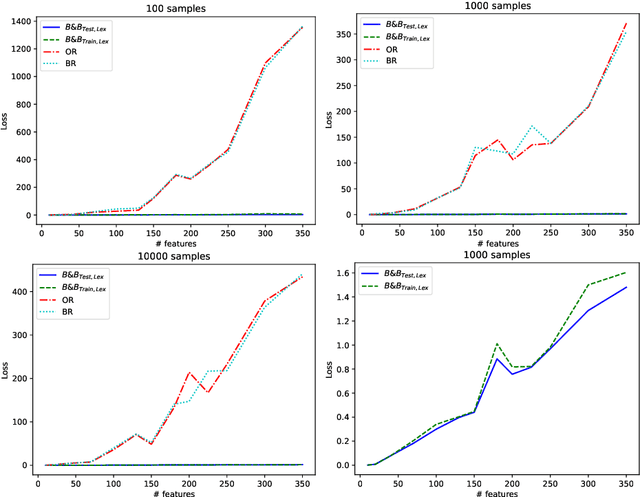
Machine learning models are widely used for real-world applications, such as document analysis and vision. Constrained machine learning problems are problems where learned models have to both be accurate and respect constraints. For continuous convex constraints, many works have been proposed, but learning under combinatorial constraints is still a hard problem. The goal of this paper is to broaden the modeling capacity of constrained machine learning problems by incorporating existing work from combinatorial optimization. We propose first a general framework called BaGeL (Branch, Generate and Learn) which applies Branch and Bound to constrained learning problems where a learning problem is generated and trained at each node until only valid models are obtained. Because machine learning has specific requirements, we also propose an extended table constraint to split the space of hypotheses. We validate the approach on two examples: a linear regression under configuration constraints and a non-negative matrix factorization with prior knowledge for latent semantics analysis.

A Complete Solver for Constraint Games

Game Theory studies situations in which multiple agents having conflicting objectives have to reach a collective decision. The question of a compact representation language for agents utility function is of crucial importance since the classical representation of a $n$-players game is given by a $n$-dimensional matrix of exponential size for each player. In this paper we use the framework of Constraint Games in which CSP are used to represent utilities. Constraint Programming --including global constraints-- allows to easily give a compact and elegant model to many useful games. Constraint Games come in two flavors: Constraint Satisfaction Games and Constraint Optimization Games, the first one using satisfaction to define boolean utilities. In addition to multimatrix games, it is also possible to model more complex games where hard constraints forbid certain situations. In this paper we study complete search techniques and show that our solver using the compact representation of Constraint Games is faster than the classical game solver Gambit by one to two orders of magnitude.