A new Linear Time Bi-level $\ell_{1,\infty}$ projection ; Application to the sparsification of auto-encoders neural networks

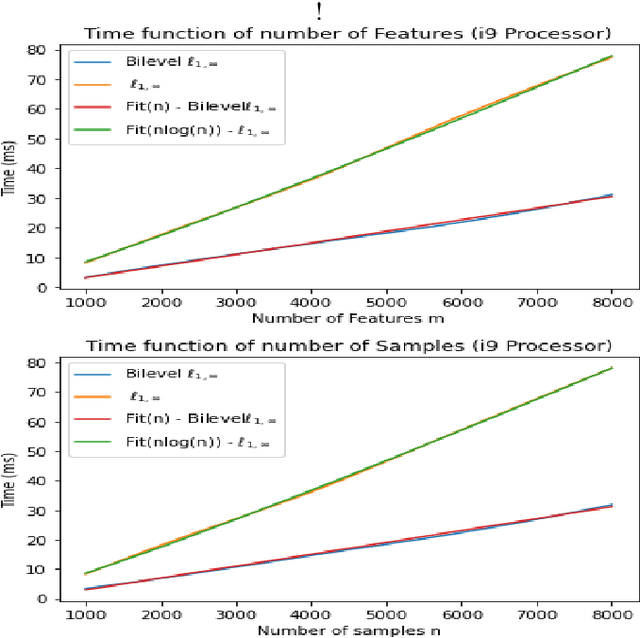
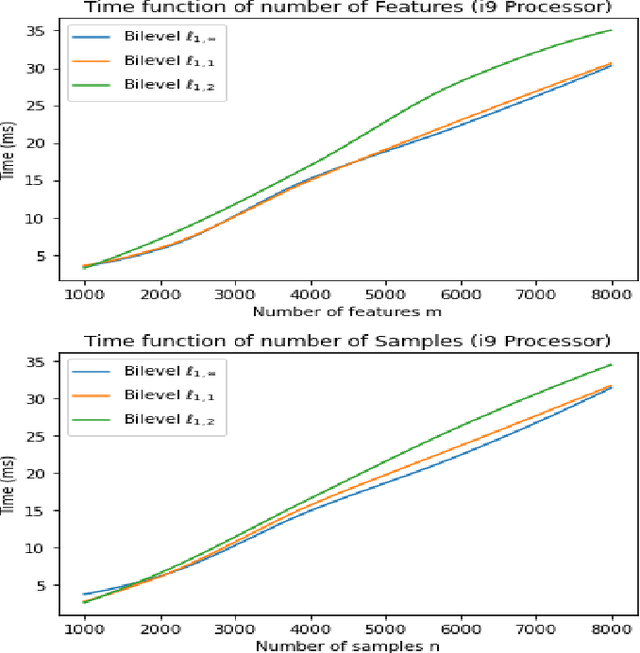
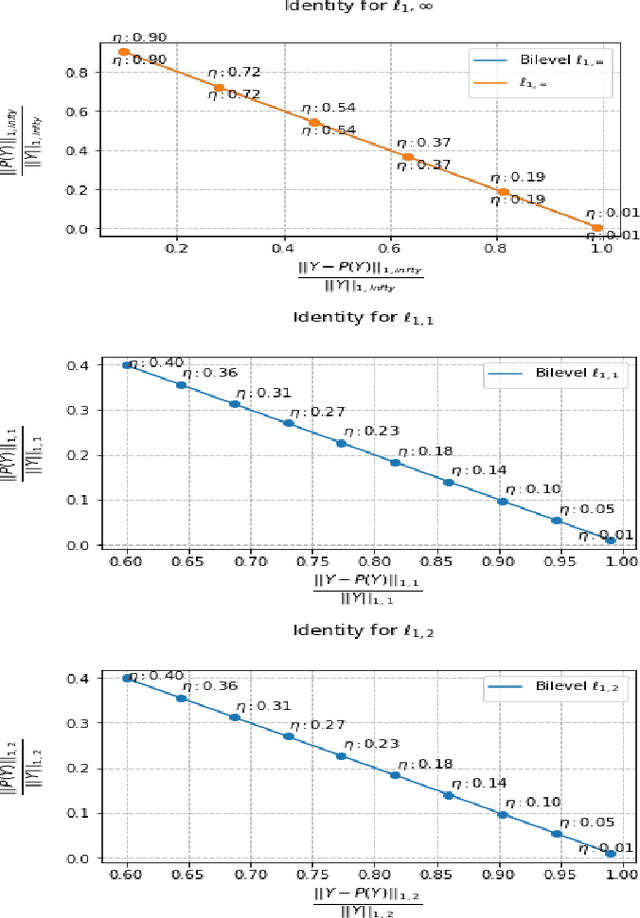
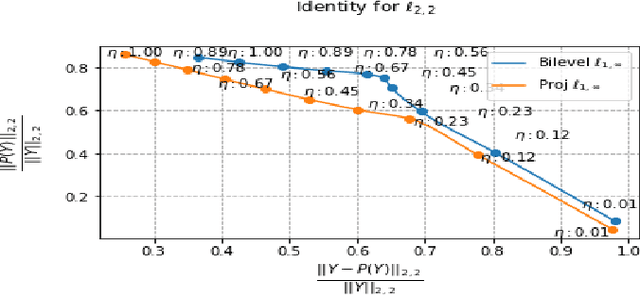
The $\ell_{1,\infty}$ norm is an efficient-structured projection, but the complexity of the best algorithm is, unfortunately, $\mathcal{O}\big(n m \log(n m)\big)$ for a matrix $n\times m$.\\ In this paper, we propose a new bi-level projection method, for which we show that the time complexity for the $\ell_{1,\infty}$ norm is only $\mathcal{O}\big(n m \big)$ for a matrix $n\times m$. Moreover, we provide a new $\ell_{1,\infty}$ identity with mathematical proof and experimental validation. Experiments show that our bi-level $\ell_{1,\infty}$ projection is $2.5$ times faster than the actual fastest algorithm and provides the best sparsity while keeping the same accuracy in classification applications.

Multi-level projection with exponential parallel speedup; Application to sparse auto-encoders neural networks

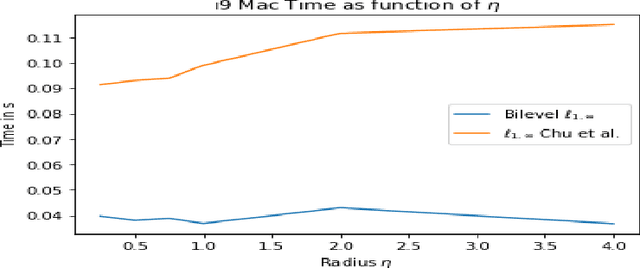
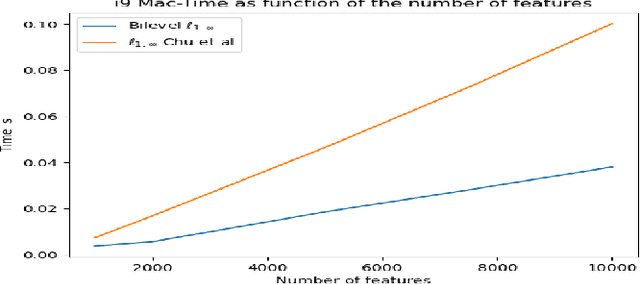
The $\ell_{1,\infty}$ norm is an efficient structured projection but the complexity of the best algorithm is unfortunately $\mathcal{O}\big(n m \log(n m)\big)$ for a matrix in $\mathbb{R}^{n\times m}$. In this paper, we propose a new bi-level projection method for which we show that the time complexity for the $\ell_{1,\infty}$ norm is only $\mathcal{O}\big(n m \big)$ for a matrix in $\mathbb{R}^{n\times m}$, and $\mathcal{O}\big(n + m \big)$ with full parallel power. We generalize our method to tensors and we propose a new multi-level projection, having an induced decomposition that yields a linear parallel speedup up to an exponential speedup factor, resulting in a time complexity lower-bounded by the sum of the dimensions. Experiments show that our bi-level $\ell_{1,\infty}$ projection is $2.5$ times faster than the actual fastest algorithm provided by \textit{Chu et. al.} while providing same accuracy and better sparsity in neural networks applications.

A Constraint Programming Model for Scheduling the Unloading of Trains in Ports: Extended

In this paper, we propose a model to schedule the next 24 hours of operations in a bulk cargo port to unload bulk cargo trains onto stockpiles. It is a problem that includes multiple parts such as splitting long trains into shorter ones and the routing of bulk material through a configurable network of conveyors to the stockpiles. Managing such trains (up to three kilometers long) also requires specialized equipment. The real world nature of the problem specification implies the necessity to manage heterogeneous data. Indeed, when new equipment is added (e.g. dumpers) or a new type of wagon comes in use, older or different equipment will still be in use as well. All these details need to be accounted for. In fact, avoiding a full deadlock of the facility after a new but ineffective schedule is produced. In this paper, we provide a detailed presentation of this real world problem and its associated data. This allows us to propose an effective constraint programming model to solve this problem. We also discuss the model design and the different implementations of the propagators that we used in practice. Finally, we show how this model, coupled with a large neighborhood search, was able to find 24 hour schedules efficiently.

Near-Linear Time Projection onto the $\ell_{1,\infty}$ Ball; Application to Sparse Autoencoders

Looking for sparsity is nowadays crucial to speed up the training of large-scale neural networks. Projections onto the $\ell_{1,2}$ and $\ell_{1,\infty}$ are among the most efficient techniques to sparsify and reduce the overall cost of neural networks. In this paper, we introduce a new projection algorithm for the $\ell_{1,\infty}$ norm ball. The worst-case time complexity of this algorithm is $\mathcal{O}\big(nm+J\log(nm)\big)$ for a matrix in $\mathbb{R}^{n\times m}$. $J$ is a term that tends to 0 when the sparsity is high, and to $nm$ when the sparsity is low. Its implementation is easy and it is guaranteed to converge to the exact solution in a finite time. Moreover, we propose to incorporate the $\ell_{1,\infty}$ ball projection while training an autoencoder to enforce feature selection and sparsity of the weights. Sparsification appears in the encoder to primarily do feature selection due to our application in biology, where only a very small part ($<2\%$) of the data is relevant. We show that both in the biological case and in the general case of sparsity that our method is the fastest.

Constrained Machine Learning: The Bagel Framework

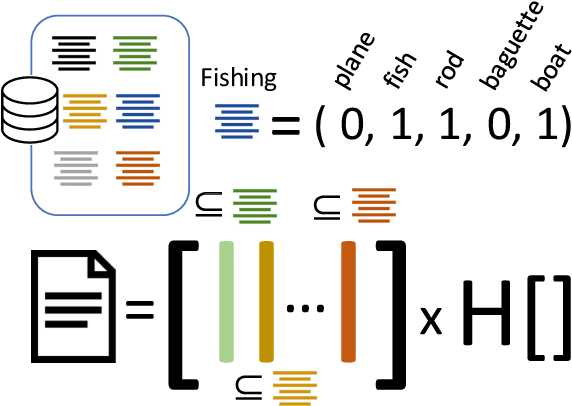
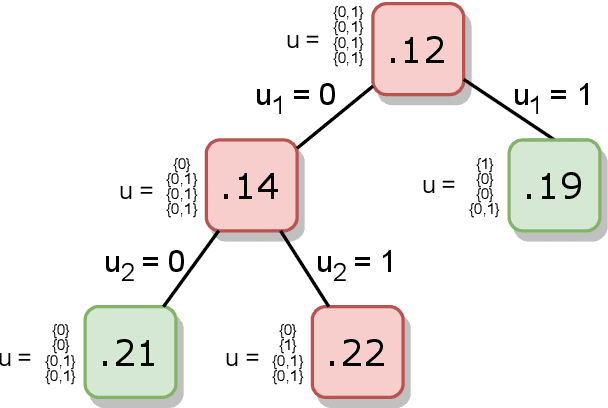
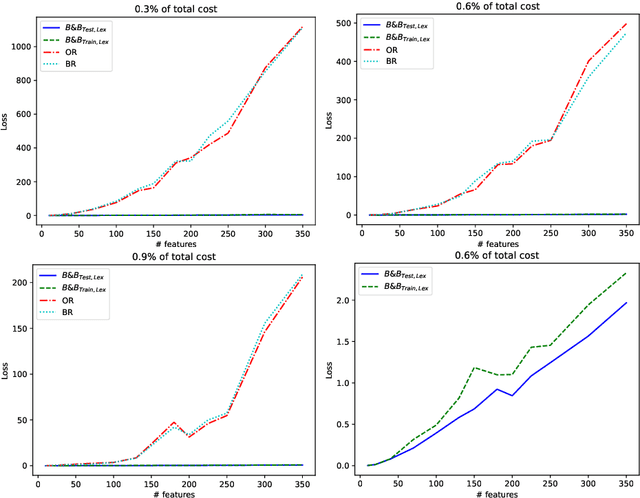
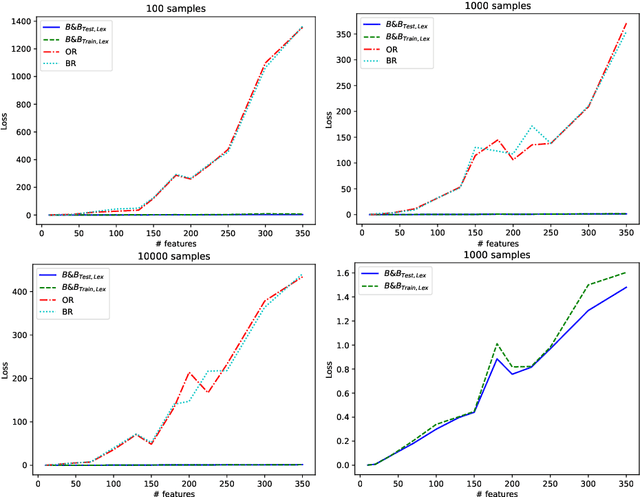
Machine learning models are widely used for real-world applications, such as document analysis and vision. Constrained machine learning problems are problems where learned models have to both be accurate and respect constraints. For continuous convex constraints, many works have been proposed, but learning under combinatorial constraints is still a hard problem. The goal of this paper is to broaden the modeling capacity of constrained machine learning problems by incorporating existing work from combinatorial optimization. We propose first a general framework called BaGeL (Branch, Generate and Learn) which applies Branch and Bound to constrained learning problems where a learning problem is generated and trained at each node until only valid models are obtained. Because machine learning has specific requirements, we also propose an extended table constraint to split the space of hypotheses. We validate the approach on two examples: a linear regression under configuration constraints and a non-negative matrix factorization with prior knowledge for latent semantics analysis.

Efficient Projection Algorithms onto the Weighted l1 Ball

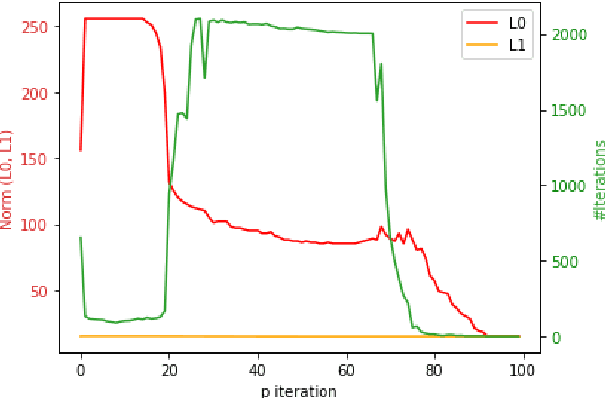
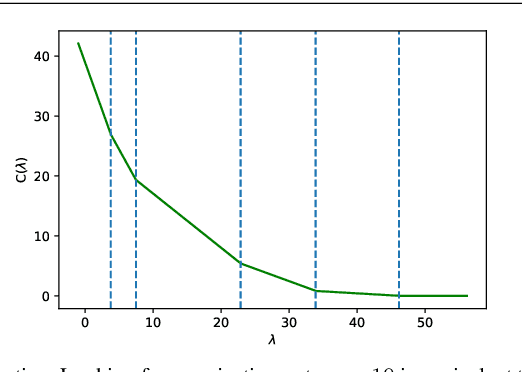
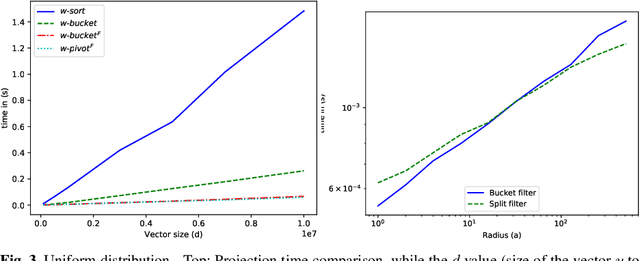
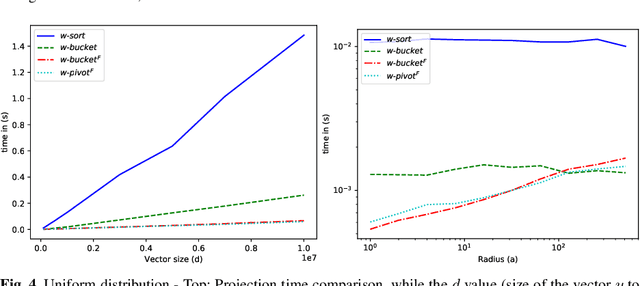
Projected gradient descent has been proved efficient in many optimization and machine learning problems. The weighted $\ell_1$ ball has been shown effective in sparse system identification and features selection. In this paper we propose three new efficient algorithms for projecting any vector of finite length onto the weighted $\ell_1$ ball. The first two algorithms have a linear worst case complexity. The third one has a highly competitive performances in practice but the worst case has a quadratic complexity. These new algorithms are efficient tools for machine learning methods based on projected gradient descent such as compress sensing, feature selection. We illustrate this effectiveness by adapting an efficient compress sensing algorithm to weighted projections. We demonstrate the efficiency of our new algorithms on benchmarks using very large vectors. For instance, it requires only 8 ms, on an Intel I7 3rd generation, for projecting vectors of size $10^7$.

Compact-Table: Efficiently Filtering Table Constraints with Reversible Sparse Bit-Sets

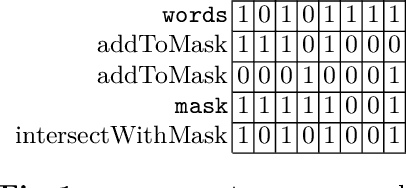
In this paper, we describe Compact-Table (CT), a bitwise algorithm to enforce Generalized Arc Consistency (GAC) on table con- straints. Although this algorithm is the default propagator for table constraints in or-tools and OscaR, two publicly available CP solvers, it has never been described so far. Importantly, CT has been recently improved further with the introduction of residues, resetting operations and a data-structure called reversible sparse bit-set, used to maintain tables of supports (following the idea of tabular reduction): tuples are invalidated incrementally on value removals by means of bit-set operations. The experimentation that we have conducted with OscaR shows that CT outperforms state-of-the-art algorithms STR2, STR3, GAC4R, MDD4R and AC5-TC on standard benchmarks.

Relations between MDDs and Tuples and Dynamic Modifications of MDDs based constraints

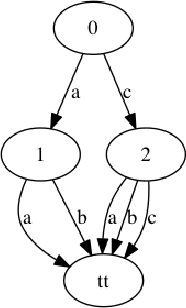
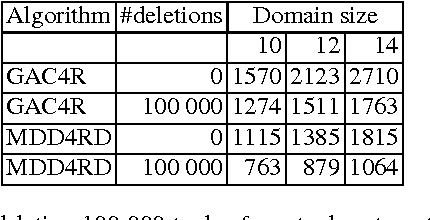
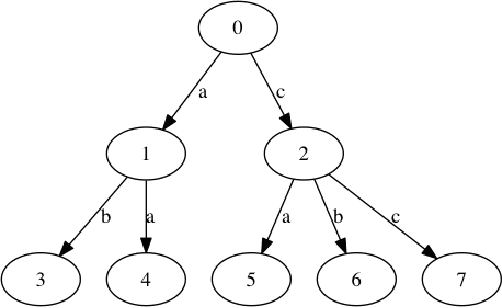
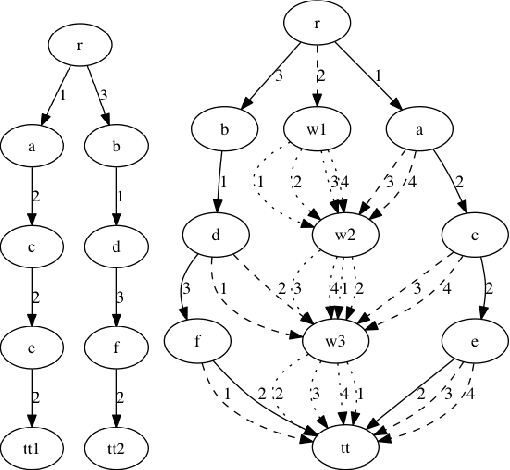
We study the relations between Multi-valued Decision Diagrams (MDD) and tuples (i.e. elements of the Cartesian Product of variables). First, we improve the existing methods for transforming a set of tuples, Global Cut Seeds, sequences of tuples into MDDs. Then, we present some in-place algorithms for adding and deleting tuples from an MDD. Next, we consider an MDD constraint which is modified during the search by deleting some tuples. We give an algorithm which adapts MDD-4R to these dynamic and persistent modifications. Some experiments show that MDD constraints are competitive with Table constraints.