Intertwining CP and NLP: The Generation of Unreasonably Constrained Sentences

Constrained text generation remains a challenging task, particularly when dealing with hard constraints. Traditional Natural Language Processing (NLP) approaches prioritize generating meaningful and coherent output. Also, the current state-of-the-art methods often lack the expressiveness and constraint satisfaction capabilities to handle such tasks effectively. This paper presents the Constraints First Framework to remedy this issue. This framework considers a constrained text generation problem as a discrete combinatorial optimization problem. It is solved by a constraint programming method that combines linguistic properties (e.g., n-grams or language level) with other more classical constraints (e.g., the number of characters, syllables, or words). Eventually, a curation phase allows for selecting the best-generated sentences according to perplexity using a large language model. The effectiveness of this approach is demonstrated by tackling a new more tediously constrained text generation problem: the iconic RADNER sentences problem. This problem aims to generate sentences respecting a set of quite strict rules defined by their use in vision and clinical research. Thanks to our CP-based approach, many new strongly constrained sentences have been successfully generated in an automatic manner. This highlights the potential of our approach to handle unreasonably constrained text generation scenarios.

Markov Constraint as Large Language Model Surrogate

This paper presents NgramMarkov, a variant of the Markov constraints. It is dedicated to text generation in constraint programming (CP). It involves a set of n-grams (i.e., sequence of n words) associated with probabilities given by a large language model (LLM). It limits the product of the probabilities of the n-gram of a sentence. The propagator of this constraint can be seen as an extension of the ElementaryMarkov constraint propagator, incorporating the LLM distribution instead of the maximum likelihood estimation of n-grams. It uses a gliding threshold, i.e., it rejects n-grams whose local probabilities are too low, to guarantee balanced solutions. It can also be combined with a "look-ahead" approach to remove n-grams that are very unlikely to lead to acceptable sentences for a fixed-length horizon. This idea is based on the MDDMarkovProcess constraint propagator, but without explicitly using an MDD (Multi-Valued Decision Diagram). The experimental results show that the generated text is valued in a similar way to the LLM perplexity function. Using this new constraint dramatically reduces the number of candidate sentences produced, improves computation times, and allows larger corpora or smaller n-grams to be used. A real-world problem has been solved for the first time using 4-grams instead of 5-grams.

Constraints First: A New MDD-based Model to Generate Sentences Under Constraints

This paper introduces a new approach to generating strongly constrained texts. We consider standardized sentence generation for the typical application of vision screening. To solve this problem, we formalize it as a discrete combinatorial optimization problem and utilize multivalued decision diagrams (MDD), a well-known data structure to deal with constraints. In our context, one key strength of MDD is to compute an exhaustive set of solutions without performing any search. Once the sentences are obtained, we apply a language model (GPT-2) to keep the best ones. We detail this for English and also for French where the agreement and conjugation rules are known to be more complex. Finally, with the help of GPT-2, we get hundreds of bona-fide candidate sentences. When compared with the few dozen sentences usually available in the well-known vision screening test (MNREAD), this brings a major breakthrough in the field of standardized sentence generation. Also, as it can be easily adapted for other languages, it has the potential to make the MNREAD test even more valuable and usable. More generally, this paper highlights MDD as a convincing alternative for constrained text generation, especially when the constraints are hard to satisfy, but also for many other prospects.

Imposing edges in Minimum Spanning Tree

We are interested in the consequences of imposing edges in $T$ a minimum spanning tree. We prove that the sum of the replacement costs in $T$ of the imposed edges is a lower bounds of the additional costs. More precisely if r-cost$(T,e)$ is the replacement cost of the edge $e$, we prove that if we impose a set $I$ of nontree edges of $T$ then $\sum_{e \in I} $ r-cost$(T,e) \leq$ cost$(T_{e \in I})$, where $I$ is the set of imposed edges and $T_{e \in I}$ a minimum spanning tree containing all the edges of $I$.

Compact-Table: Efficiently Filtering Table Constraints with Reversible Sparse Bit-Sets

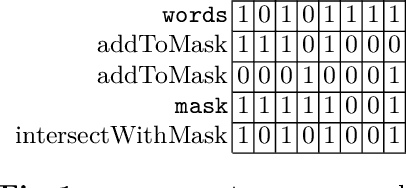
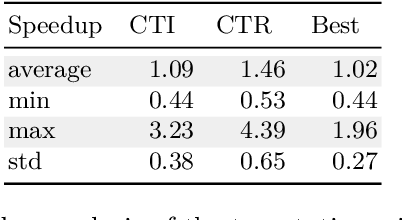
In this paper, we describe Compact-Table (CT), a bitwise algorithm to enforce Generalized Arc Consistency (GAC) on table con- straints. Although this algorithm is the default propagator for table constraints in or-tools and OscaR, two publicly available CP solvers, it has never been described so far. Importantly, CT has been recently improved further with the introduction of residues, resetting operations and a data-structure called reversible sparse bit-set, used to maintain tables of supports (following the idea of tabular reduction): tuples are invalidated incrementally on value removals by means of bit-set operations. The experimentation that we have conducted with OscaR shows that CT outperforms state-of-the-art algorithms STR2, STR3, GAC4R, MDD4R and AC5-TC on standard benchmarks.

Parallel Strategies Selection

We consider the problem of selecting the best variable-value strategy for solving a given problem in constraint programming. We show that the recent Embarrassingly Parallel Search method (EPS) can be used for this purpose. EPS proposes to solve a problem by decomposing it in a lot of subproblems and to give them on-demand to workers which run in parallel. Our method uses a part of these subproblems as a simple sample as defined in statistics for comparing some strategies in order to select the most promising one that will be used for solving the remaining subproblems. For each subproblem of the sample, the parallelism helps us to control the running time of the strategies because it gives us the possibility to introduce timeouts by stopping a strategy when it requires more than twice the time of the best one. Thus, we can deal with the great disparity in solving times for the strategies. The selections we made are based on the Wilcoxon signed rank tests because no assumption has to be made on the distribution of the solving times and because these tests can deal with the censored data that we obtain after introducing timeouts. The experiments we performed on a set of classical benchmarks for satisfaction and optimization problems show that our method obtain good performance by selecting almost all the time the best variable-value strategy and by almost never choosing a variable-value strategy which is dramatically slower than the best one. Our method also outperforms the portfolio approach consisting in running some strategies in parallel and is competitive with the multi armed bandit framework.

Relations between MDDs and Tuples and Dynamic Modifications of MDDs based constraints

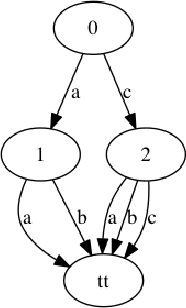
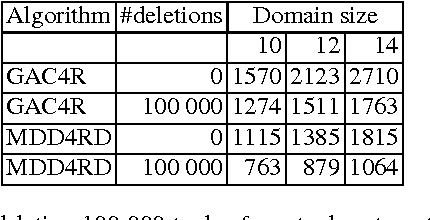
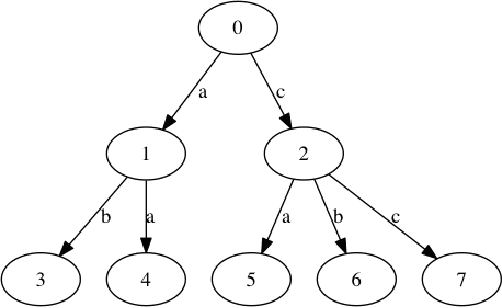
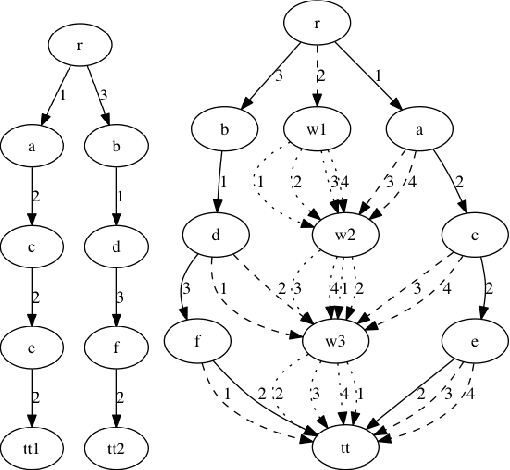
We study the relations between Multi-valued Decision Diagrams (MDD) and tuples (i.e. elements of the Cartesian Product of variables). First, we improve the existing methods for transforming a set of tuples, Global Cut Seeds, sequences of tuples into MDDs. Then, we present some in-place algorithms for adding and deleting tuples from an MDD. Next, we consider an MDD constraint which is modified during the search by deleting some tuples. We give an algorithm which adapts MDD-4R to these dynamic and persistent modifications. Some experiments show that MDD constraints are competitive with Table constraints.