Efficient Projection Algorithms onto the Weighted l1 Ball
Paper and Code
Sep 07, 2020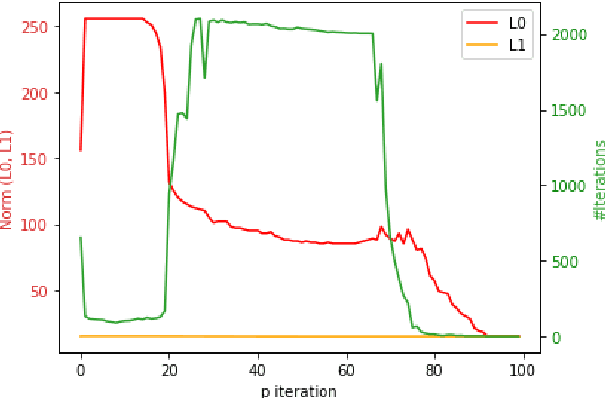
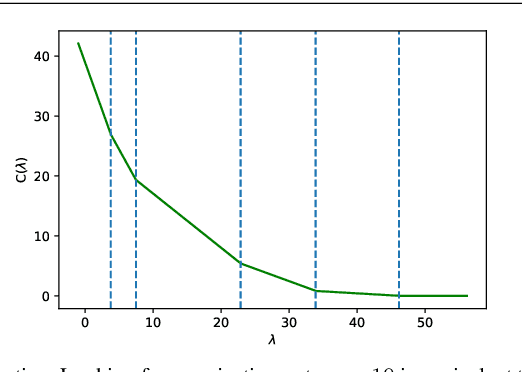
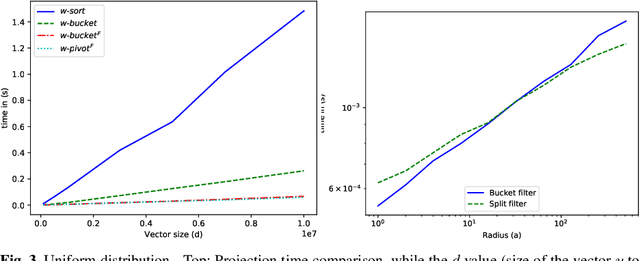
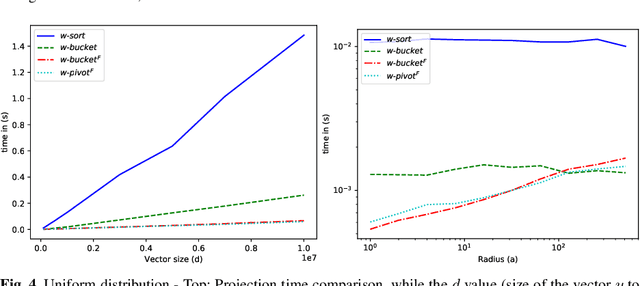
Projected gradient descent has been proved efficient in many optimization and machine learning problems. The weighted $\ell_1$ ball has been shown effective in sparse system identification and features selection. In this paper we propose three new efficient algorithms for projecting any vector of finite length onto the weighted $\ell_1$ ball. The first two algorithms have a linear worst case complexity. The third one has a highly competitive performances in practice but the worst case has a quadratic complexity. These new algorithms are efficient tools for machine learning methods based on projected gradient descent such as compress sensing, feature selection. We illustrate this effectiveness by adapting an efficient compress sensing algorithm to weighted projections. We demonstrate the efficiency of our new algorithms on benchmarks using very large vectors. For instance, it requires only 8 ms, on an Intel I7 3rd generation, for projecting vectors of size $10^7$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge