A new Linear Time Bi-level $\ell_{1,\infty}$ projection ; Application to the sparsification of auto-encoders neural networks

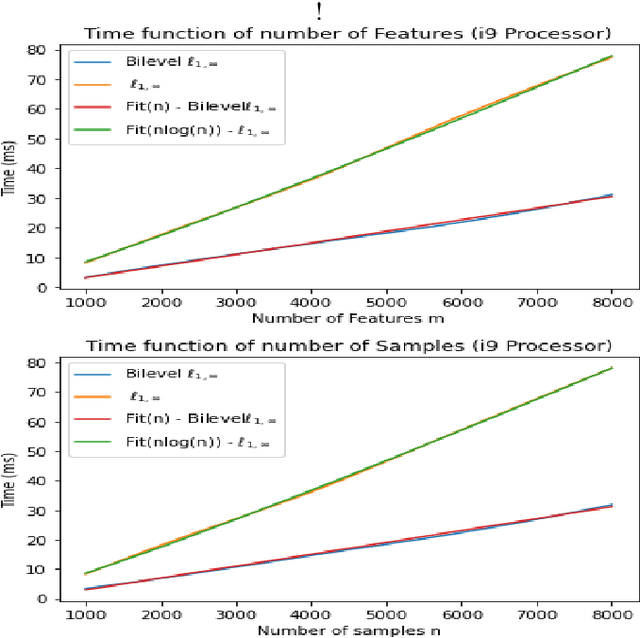
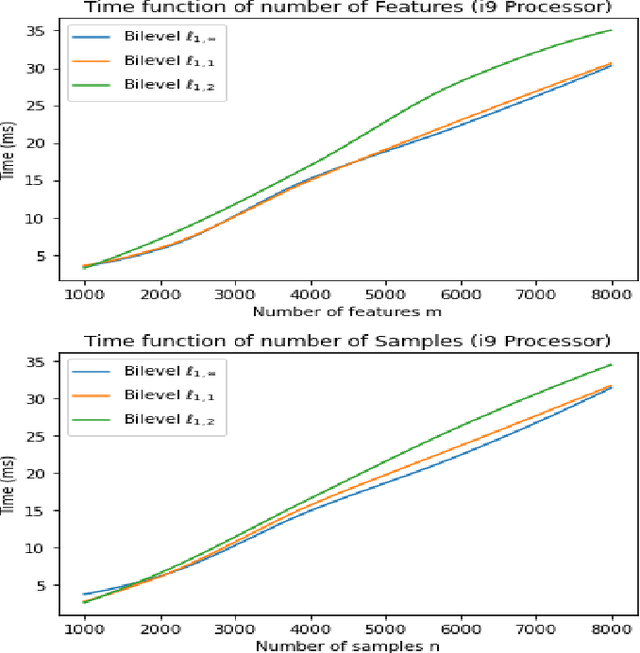
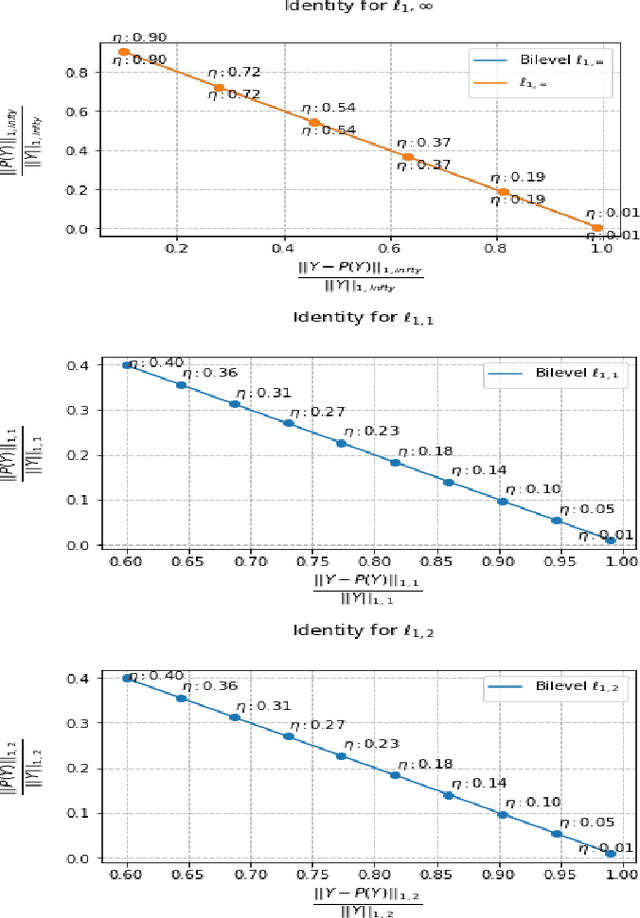
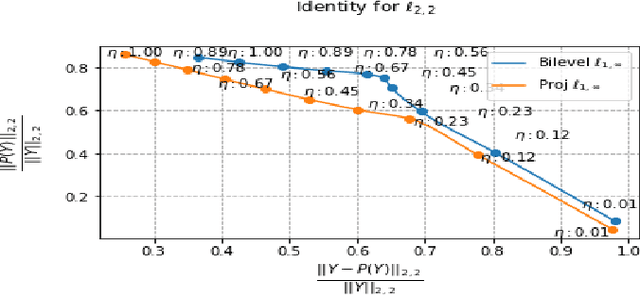
The $\ell_{1,\infty}$ norm is an efficient-structured projection, but the complexity of the best algorithm is, unfortunately, $\mathcal{O}\big(n m \log(n m)\big)$ for a matrix $n\times m$.\\ In this paper, we propose a new bi-level projection method, for which we show that the time complexity for the $\ell_{1,\infty}$ norm is only $\mathcal{O}\big(n m \big)$ for a matrix $n\times m$. Moreover, we provide a new $\ell_{1,\infty}$ identity with mathematical proof and experimental validation. Experiments show that our bi-level $\ell_{1,\infty}$ projection is $2.5$ times faster than the actual fastest algorithm and provides the best sparsity while keeping the same accuracy in classification applications.

Multi-level projection with exponential parallel speedup; Application to sparse auto-encoders neural networks

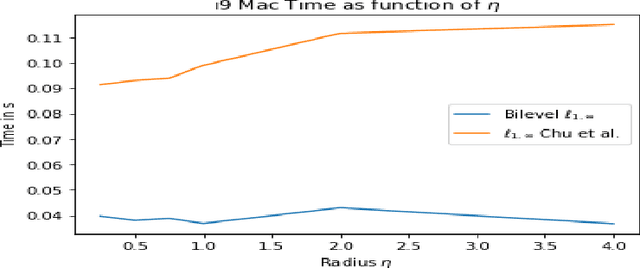
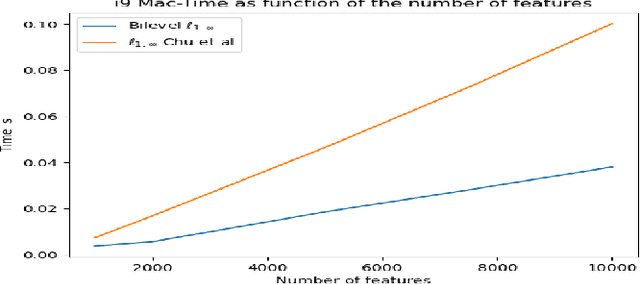
The $\ell_{1,\infty}$ norm is an efficient structured projection but the complexity of the best algorithm is unfortunately $\mathcal{O}\big(n m \log(n m)\big)$ for a matrix in $\mathbb{R}^{n\times m}$. In this paper, we propose a new bi-level projection method for which we show that the time complexity for the $\ell_{1,\infty}$ norm is only $\mathcal{O}\big(n m \big)$ for a matrix in $\mathbb{R}^{n\times m}$, and $\mathcal{O}\big(n + m \big)$ with full parallel power. We generalize our method to tensors and we propose a new multi-level projection, having an induced decomposition that yields a linear parallel speedup up to an exponential speedup factor, resulting in a time complexity lower-bounded by the sum of the dimensions. Experiments show that our bi-level $\ell_{1,\infty}$ projection is $2.5$ times faster than the actual fastest algorithm provided by \textit{Chu et. al.} while providing same accuracy and better sparsity in neural networks applications.

Near-Linear Time Projection onto the $\ell_{1,\infty}$ Ball; Application to Sparse Autoencoders

Looking for sparsity is nowadays crucial to speed up the training of large-scale neural networks. Projections onto the $\ell_{1,2}$ and $\ell_{1,\infty}$ are among the most efficient techniques to sparsify and reduce the overall cost of neural networks. In this paper, we introduce a new projection algorithm for the $\ell_{1,\infty}$ norm ball. The worst-case time complexity of this algorithm is $\mathcal{O}\big(nm+J\log(nm)\big)$ for a matrix in $\mathbb{R}^{n\times m}$. $J$ is a term that tends to 0 when the sparsity is high, and to $nm$ when the sparsity is low. Its implementation is easy and it is guaranteed to converge to the exact solution in a finite time. Moreover, we propose to incorporate the $\ell_{1,\infty}$ ball projection while training an autoencoder to enforce feature selection and sparsity of the weights. Sparsification appears in the encoder to primarily do feature selection due to our application in biology, where only a very small part ($<2\%$) of the data is relevant. We show that both in the biological case and in the general case of sparsity that our method is the fastest.

Learning sparse auto-encoders for green AI image coding

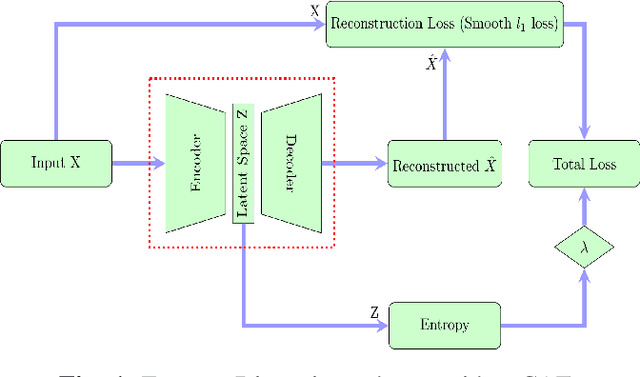
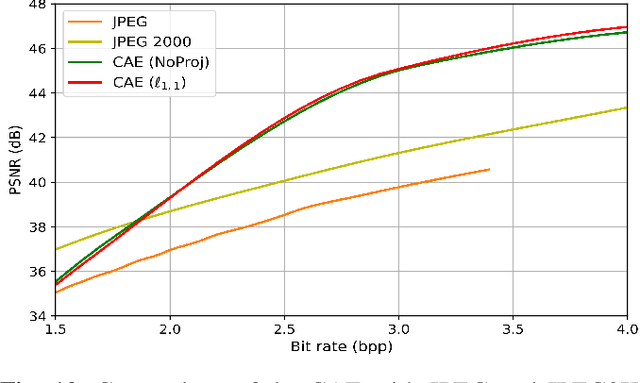
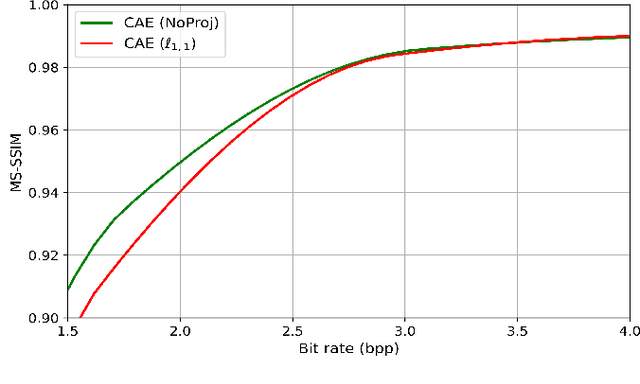
Recently, convolutional auto-encoders (CAE) were introduced for image coding. They achieved performance improvements over the state-of-the-art JPEG2000 method. However, these performances were obtained using massive CAEs featuring a large number of parameters and whose training required heavy computational power.\\ In this paper, we address the problem of lossy image compression using a CAE with a small memory footprint and low computational power usage. In order to overcome the computational cost issue, the majority of the literature uses Lagrangian proximal regularization methods, which are time consuming themselves.\\ In this work, we propose a constrained approach and a new structured sparse learning method. We design an algorithm and test it on three constraints: the classical $\ell_1$ constraint, the $\ell_{1,\infty}$ and the new $\ell_{1,1}$ constraint. Experimental results show that the $\ell_{1,1}$ constraint provides the best structured sparsity, resulting in a high reduction of memory and computational cost, with similar rate-distortion performance as with dense networks.

Semi-supervised classification using a supervised autoencoder for biomedical applications

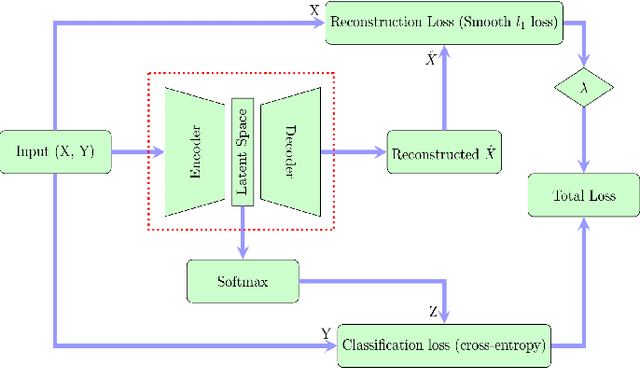
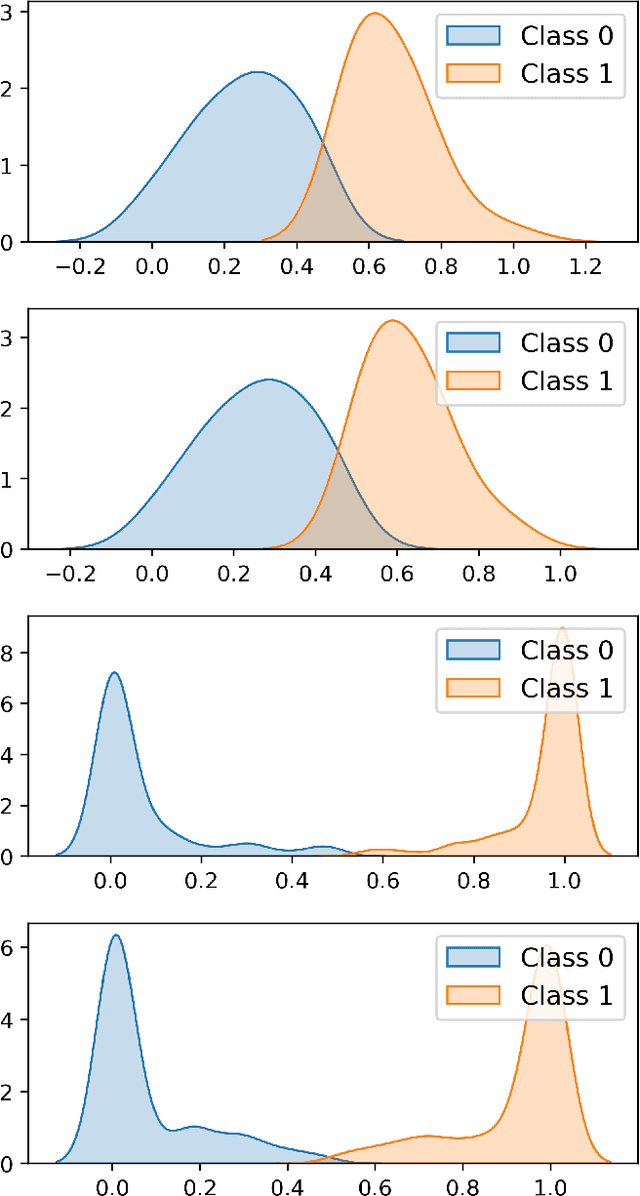
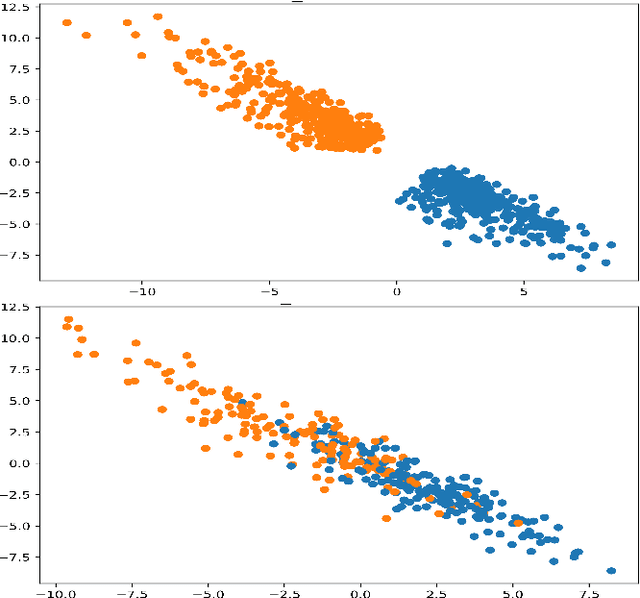
In this paper we present a new approach to solve semi-supervised classification tasks for biomedical applications, involving a supervised autoencoder network. We create a network architecture that encodes labels into the latent space of an autoencoder, and define a global criterion combining classification and reconstruction losses. We train the Semi-Supervised AutoEncoder (SSAE) on labelled data using a double descent algorithm. Then, we classify unlabelled samples using the learned network thanks to a softmax classifier applied to the latent space which provides a classification confidence score for each class. We implemented our SSAE method using the PyTorch framework for the model, optimizer, schedulers, and loss functions. We compare our semi-supervised autoencoder method (SSAE) with classical semi-supervised methods such as Label Propagation and Label Spreading, and with a Fully Connected Neural Network (FCNN). Experiments show that the SSAE outperforms Label Propagation and Spreading and the Fully Connected Neural Network both on a synthetic dataset and on two real-world biological datasets.

Efficient Projection Algorithms onto the Weighted l1 Ball

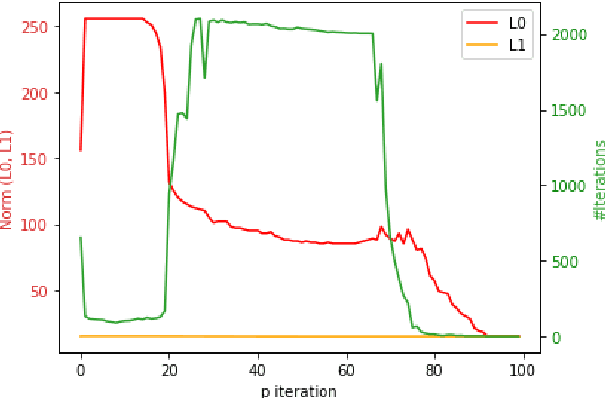
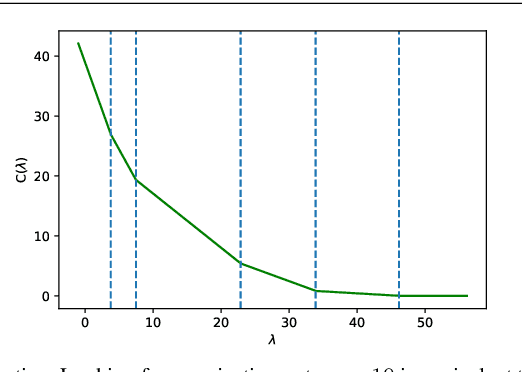
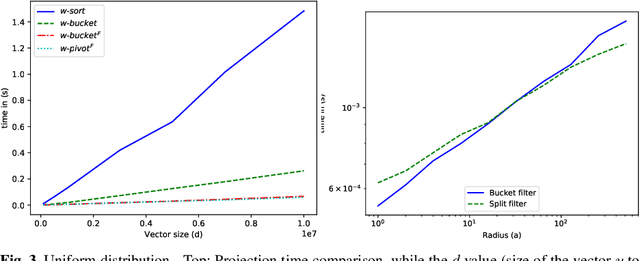
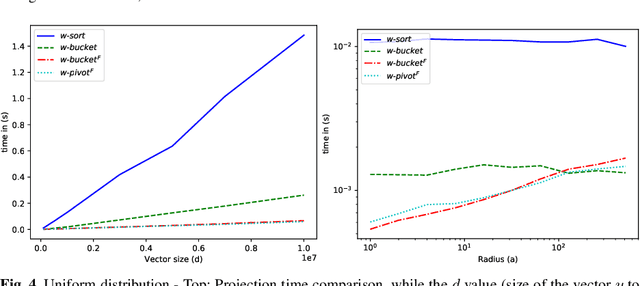
Projected gradient descent has been proved efficient in many optimization and machine learning problems. The weighted $\ell_1$ ball has been shown effective in sparse system identification and features selection. In this paper we propose three new efficient algorithms for projecting any vector of finite length onto the weighted $\ell_1$ ball. The first two algorithms have a linear worst case complexity. The third one has a highly competitive performances in practice but the worst case has a quadratic complexity. These new algorithms are efficient tools for machine learning methods based on projected gradient descent such as compress sensing, feature selection. We illustrate this effectiveness by adapting an efficient compress sensing algorithm to weighted projections. We demonstrate the efficiency of our new algorithms on benchmarks using very large vectors. For instance, it requires only 8 ms, on an Intel I7 3rd generation, for projecting vectors of size $10^7$.

Robust supervised classification and feature selection using a primal-dual method

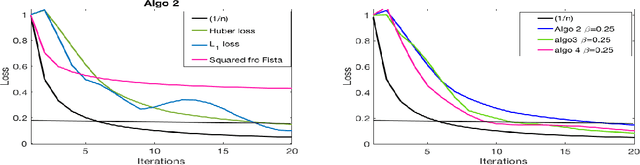
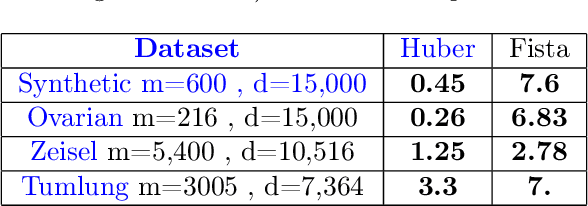
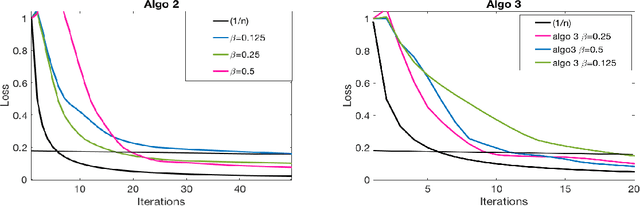
This paper deals with supervised classification and feature selection in high dimensional space. A classical approach is to project data on a low dimensional space and classify by minimizing an appropriate quadratic cost. A strict control on sparsity is moreover obtained by adding an $\ell_1$ constraint, here on the matrix of weights used for projecting the data. Tuning the sparsity bound results in selecting the relevant features for supervised classification. It is well known that using a quadratic cost is not robust to outliers. We cope with this problem by using an $\ell_1$ norm both for the constraint and for the loss function. In this case, the criterion is convex but not gradient Lipschitz anymore. Another second issue is that we optimize simultaneously the projection matrix and the centers used for classification. In this paper, we provide a novel tailored constrained primal-dual method to compute jointly selected features and classifiers. Extending our primal-dual method to other criteria is easy provided that efficient projection (on the dual ball for the loss data term) and prox (for the regularization term) algorithms are available. We illustrate such an extension in the case of a Frobenius norm for the loss term. We provide a convergence proof of our primal-dual method, and demonstrate its effectiveness on three datasets (one synthetic, two from biological data) on which we compare $\ell_1$ and $\ell_2$ costs.

Clustering with feature selection using alternating minimization, Application to computational biology

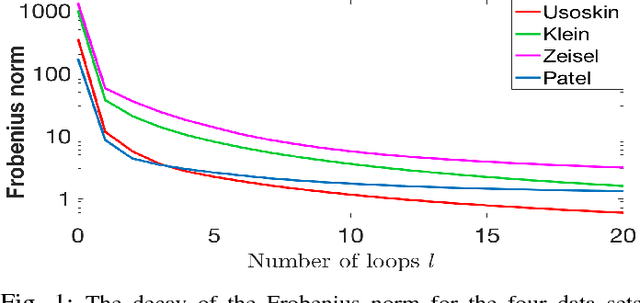
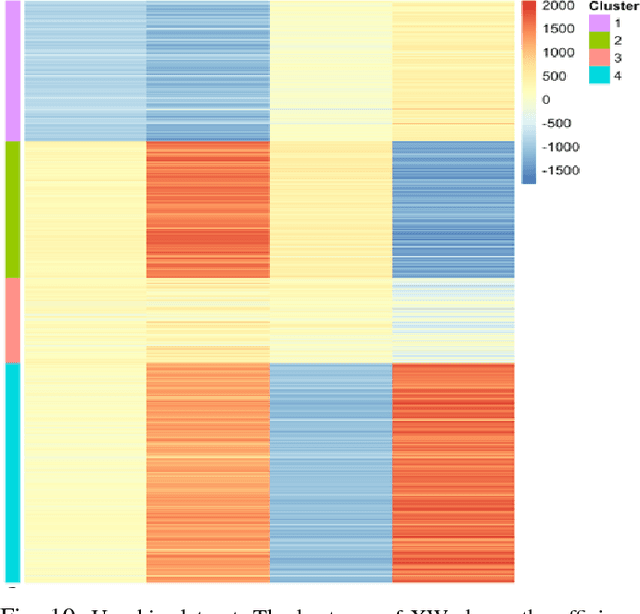
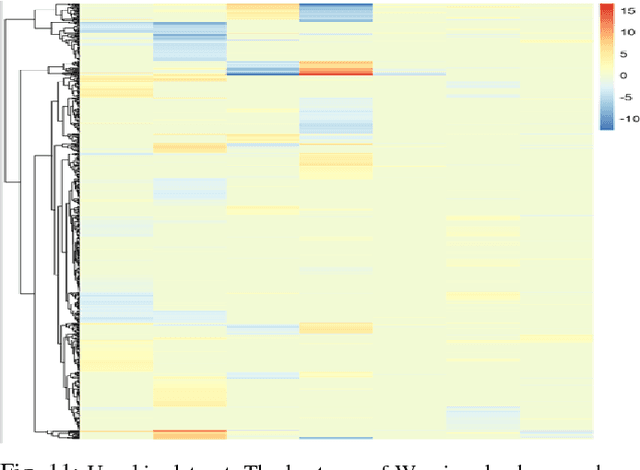
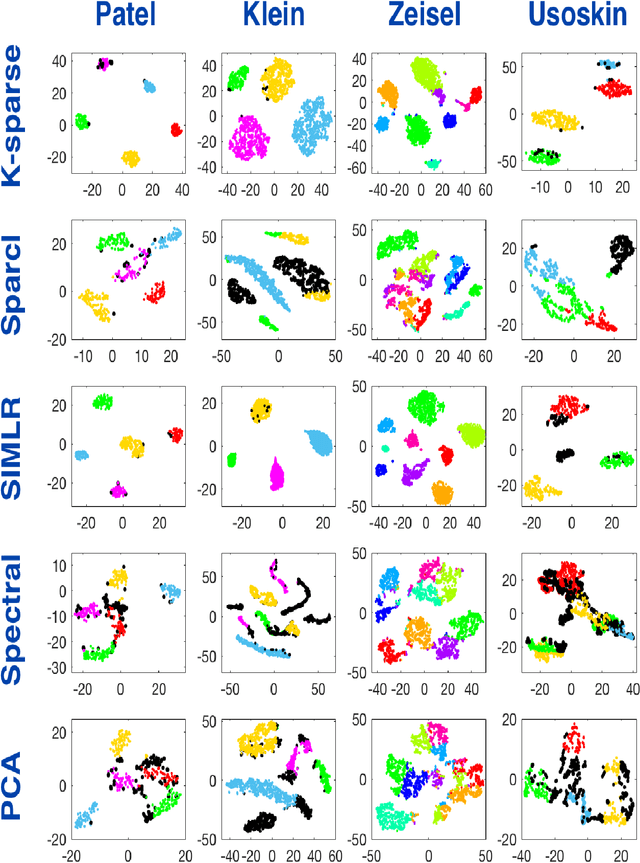
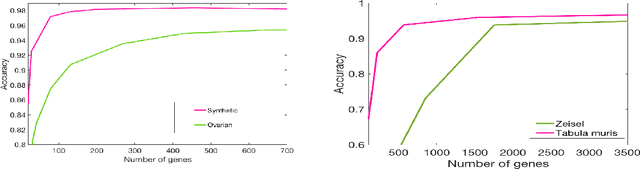
This paper deals with unsupervised clustering with feature selection. The problem is to estimate both labels and a sparse projection matrix of weights. To address this combinatorial non-convex problem maintaining a strict control on the sparsity of the matrix of weights, we propose an alternating minimization of the Frobenius norm criterion. We provide a new efficient algorithm named K-sparse which alternates k-means with projection-gradient minimization. The projection-gradient step is a method of splitting type, with exact projection on the $\ell^1$ ball to promote sparsity. The convergence of the gradient-projection step is addressed, and a preliminary analysis of the alternating minimization is made. The Frobenius norm criterion converges as the number of iterates in Algorithm K-sparse goes to infinity. Experiments on Single Cell RNA sequencing datasets show that our method significantly improves the results of PCA k-means, spectral clustering, SIMLR, and Sparcl methods, and achieves a relevant selection of genes. The complexity of K-sparse is linear in the number of samples (cells), so that the method scales up to large datasets.

Classification and regression using an outer approximation projection-gradient method

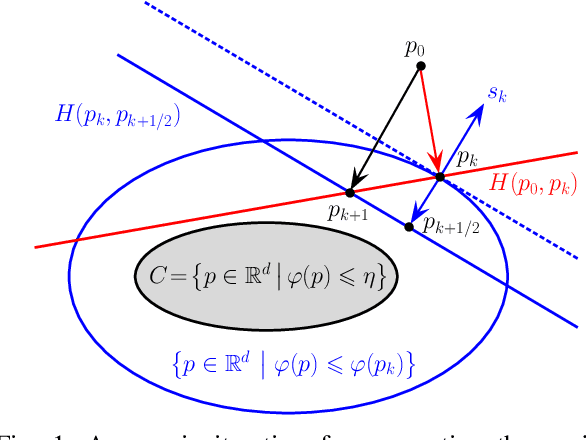
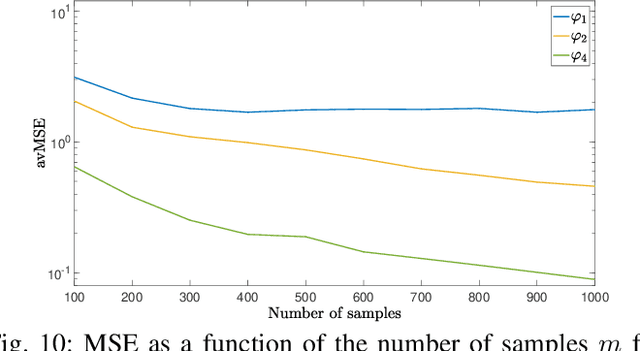
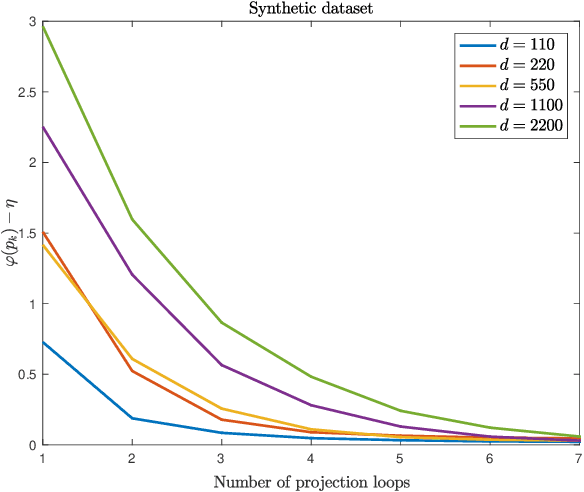
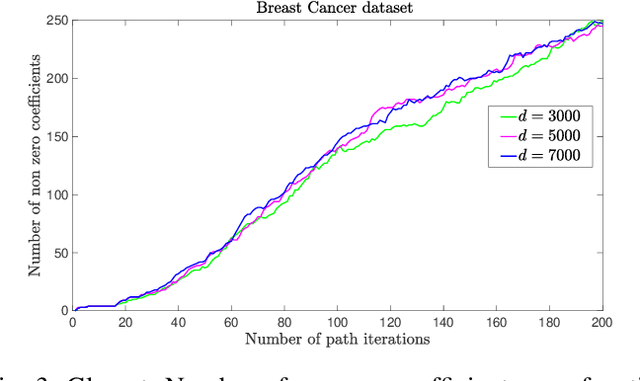
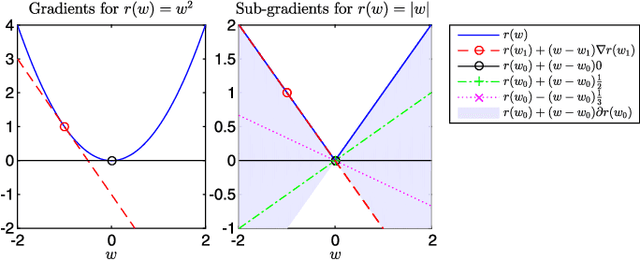
This paper deals with sparse feature selection and grouping for classification and regression. The classification or regression problems under consideration consists in minimizing a convex empirical risk function subject to an $\ell^1$ constraint, a pairwise $\ell^\infty$ constraint, or a pairwise $\ell^1$ constraint. Existing work, such as the Lasso formulation, has focused mainly on Lagrangian penalty approximations, which often require ad hoc or computationally expensive procedures to determine the penalization parameter. We depart from this approach and address the constrained problem directly via a splitting method. The structure of the method is that of the classical gradient-projection algorithm, which alternates a gradient step on the objective and a projection step onto the lower level set modeling the constraint. The novelty of our approach is that the projection step is implemented via an outer approximation scheme in which the constraint set is approximated by a sequence of simple convex sets consisting of the intersection of two half-spaces. Convergence of the iterates generated by the algorithm is established for a general smooth convex minimization problem with inequality constraints. Experiments on both synthetic and biological data show that our method outperforms penalty methods.

Non-convex regularization in remote sensing

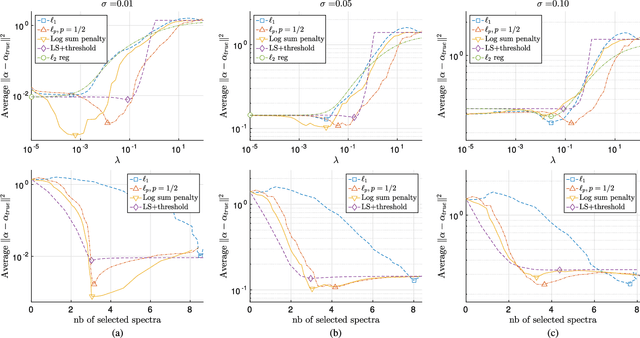
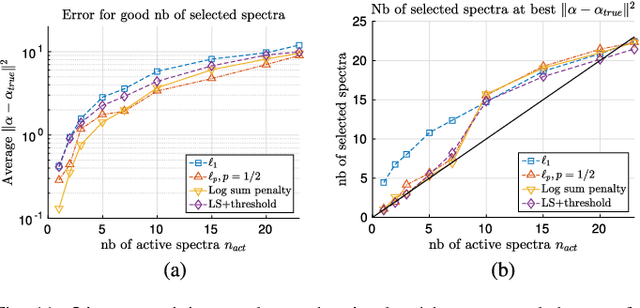
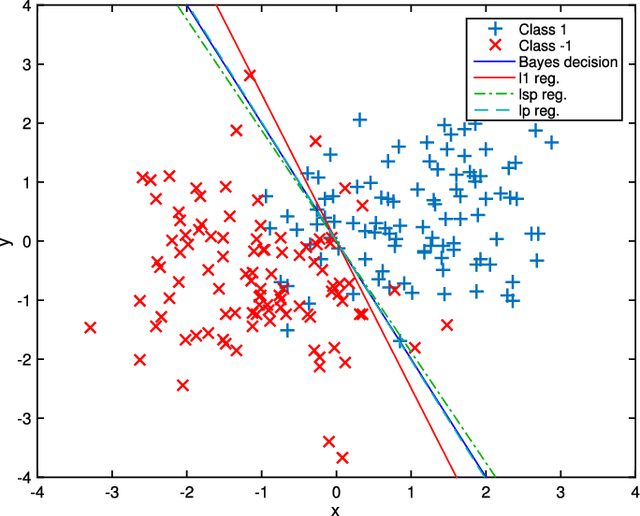
In this paper, we study the effect of different regularizers and their implications in high dimensional image classification and sparse linear unmixing. Although kernelization or sparse methods are globally accepted solutions for processing data in high dimensions, we present here a study on the impact of the form of regularization used and its parametrization. We consider regularization via traditional squared (2) and sparsity-promoting (1) norms, as well as more unconventional nonconvex regularizers (p and Log Sum Penalty). We compare their properties and advantages on several classification and linear unmixing tasks and provide advices on the choice of the best regularizer for the problem at hand. Finally, we also provide a fully functional toolbox for the community.