Lionel Fillatre
Retinal-inspired Filtering for Dynamic Image Coding
Mar 22, 2021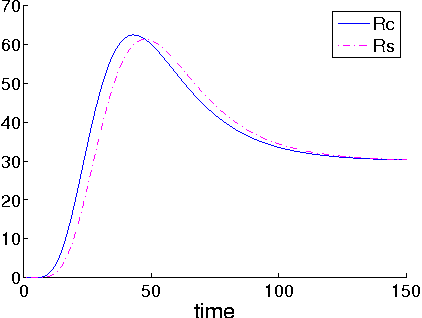



Abstract:This paper introduces a novel non-Separable sPAtioteMporal filter (non-SPAM) which enables the spatiotemporal decomposition of a still-image. The construction of this filter is inspired by the model of the retina which is able to selectively transmit information to the brain. The non-SPAM filter mimics the retinal-way to extract necessary information for a dynamic encoding/decoding system. We applied the non-SPAM filter on a still image which is flashed for a long time. We prove that the non-SPAM filter decomposes the still image over a set of time-varying difference of Gaussians, which form a frame. We simulate the analysis and synthesis system based on this frame. This system results in a progressive reconstruction of the input image. Both the theoretical and numerical results show that the quality of the reconstruction improves while the time increases.
Classification and regression using an outer approximation projection-gradient method
Mar 23, 2017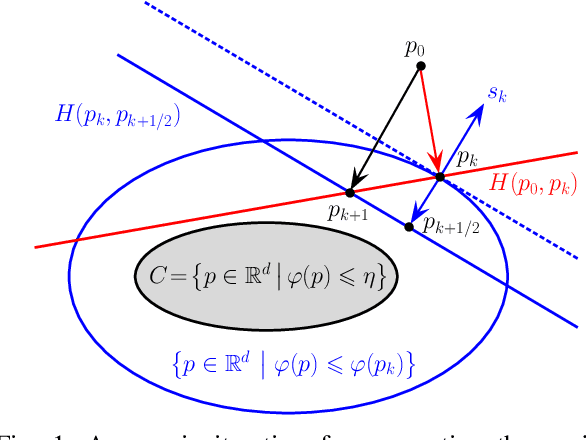
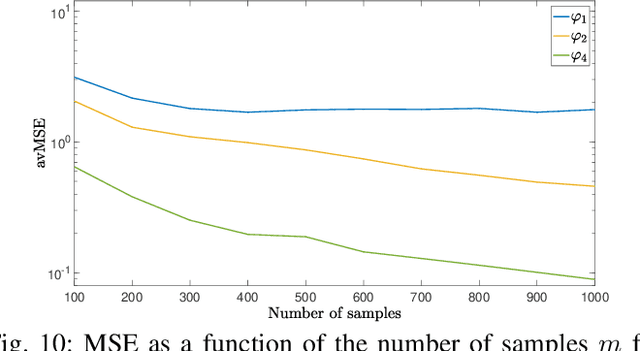
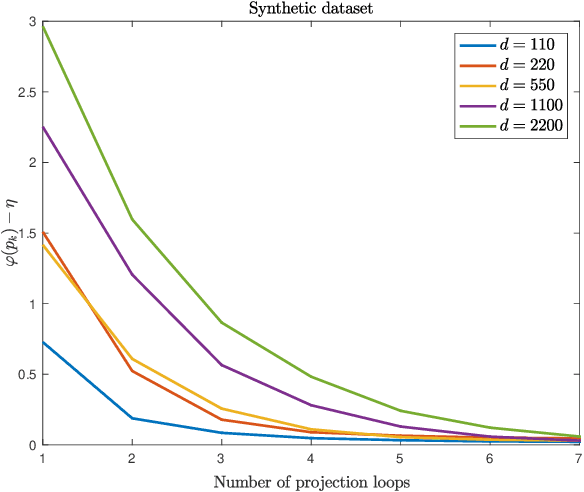
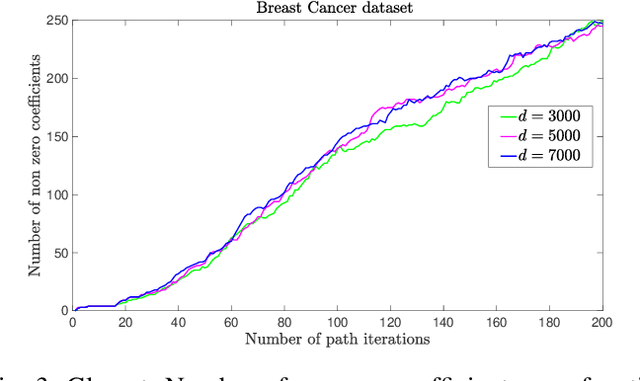
Abstract:This paper deals with sparse feature selection and grouping for classification and regression. The classification or regression problems under consideration consists in minimizing a convex empirical risk function subject to an $\ell^1$ constraint, a pairwise $\ell^\infty$ constraint, or a pairwise $\ell^1$ constraint. Existing work, such as the Lasso formulation, has focused mainly on Lagrangian penalty approximations, which often require ad hoc or computationally expensive procedures to determine the penalization parameter. We depart from this approach and address the constrained problem directly via a splitting method. The structure of the method is that of the classical gradient-projection algorithm, which alternates a gradient step on the objective and a projection step onto the lower level set modeling the constraint. The novelty of our approach is that the projection step is implemented via an outer approximation scheme in which the constraint set is approximated by a sequence of simple convex sets consisting of the intersection of two half-spaces. Convergence of the iterates generated by the algorithm is established for a general smooth convex minimization problem with inequality constraints. Experiments on both synthetic and biological data show that our method outperforms penalty methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge