Robust supervised classification and feature selection using a primal-dual method
Paper and Code
Feb 27, 2019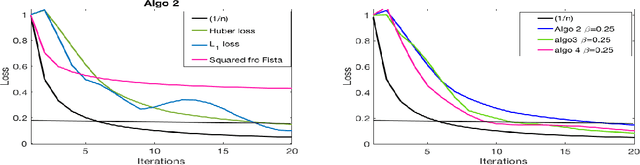
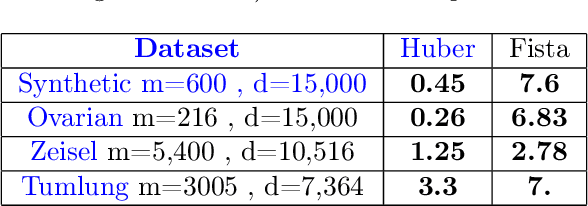
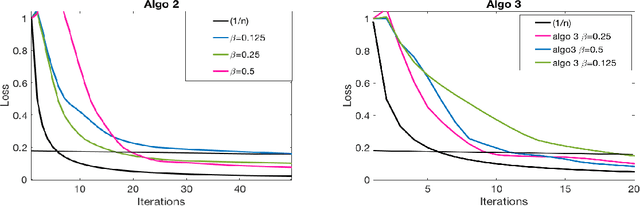
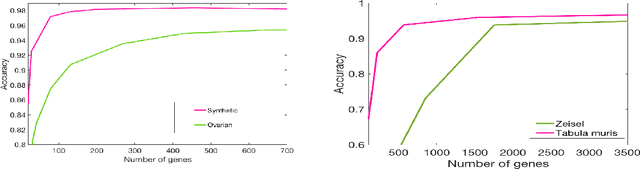
This paper deals with supervised classification and feature selection in high dimensional space. A classical approach is to project data on a low dimensional space and classify by minimizing an appropriate quadratic cost. A strict control on sparsity is moreover obtained by adding an $\ell_1$ constraint, here on the matrix of weights used for projecting the data. Tuning the sparsity bound results in selecting the relevant features for supervised classification. It is well known that using a quadratic cost is not robust to outliers. We cope with this problem by using an $\ell_1$ norm both for the constraint and for the loss function. In this case, the criterion is convex but not gradient Lipschitz anymore. Another second issue is that we optimize simultaneously the projection matrix and the centers used for classification. In this paper, we provide a novel tailored constrained primal-dual method to compute jointly selected features and classifiers. Extending our primal-dual method to other criteria is easy provided that efficient projection (on the dual ball for the loss data term) and prox (for the regularization term) algorithms are available. We illustrate such an extension in the case of a Frobenius norm for the loss term. We provide a convergence proof of our primal-dual method, and demonstrate its effectiveness on three datasets (one synthetic, two from biological data) on which we compare $\ell_1$ and $\ell_2$ costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge