Convergent plug-and-play with proximal denoiser and unconstrained regularization parameter

In this work, we present new proofs of convergence for Plug-and-Play (PnP) algorithms. PnP methods are efficient iterative algorithms for solving image inverse problems where regularization is performed by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD) or Douglas-Rachford Splitting (DRS). Recent research has explored convergence by incorporating a denoiser that writes exactly as a proximal operator. However, the corresponding PnP algorithm has then to be run with stepsize equal to $1$. The stepsize condition for nonconvex convergence of the proximal algorithm in use then translates to restrictive conditions on the regularization parameter of the inverse problem. This can severely degrade the restoration capacity of the algorithm. In this paper, we present two remedies for this limitation. First, we provide a novel convergence proof for PnP-DRS that does not impose any restrictions on the regularization parameter. Second, we examine a relaxed version of the PGD algorithm that converges across a broader range of regularization parameters. Our experimental study, conducted on deblurring and super-resolution experiments, demonstrate that both of these solutions enhance the accuracy of image restoration.

Product of Gaussian Mixture Diffusion Models

In this work we tackle the problem of estimating the density $ f_X $ of a random variable $ X $ by successive smoothing, such that the smoothed random variable $ Y $ fulfills the diffusion partial differential equation $ (\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0 $ with initial condition $ f_Y(\,\cdot\,, 0) = f_X $. We propose a product-of-experts-type model utilizing Gaussian mixture experts and study configurations that admit an analytic expression for $ f_Y (\,\cdot\,, t) $. In particular, with a focus on image processing, we derive conditions for models acting on filter-, wavelet-, and shearlet responses. Our construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show numerical results for image denoising where our models are competitive while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our models can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Explicit Diffusion of Gaussian Mixture Model Based Image Priors

In this work we tackle the problem of estimating the density $f_X$ of a random variable $X$ by successive smoothing, such that the smoothed random variable $Y$ fulfills $(\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0$, $f_Y(\,\cdot\,, 0) = f_X$. With a focus on image processing, we propose a product/fields of experts model with Gaussian mixture experts that admits an analytic expression for $f_Y (\,\cdot\,, t)$ under an orthogonality constraint on the filters. This construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show preliminary results on image denoising where our model leads to competitive results while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our model can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

A relaxed proximal gradient descent algorithm for convergent plug-and-play with proximal denoiser

This paper presents a new convergent Plug-and-Play (PnP) algorithm. PnP methods are efficient iterative algorithms for solving image inverse problems formulated as the minimization of the sum of a data-fidelity term and a regularization term. PnP methods perform regularization by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD). To ensure convergence of PnP schemes, many works study specific parametrizations of deep denoisers. However, existing results require either unverifiable or suboptimal hypotheses on the denoiser, or assume restrictive conditions on the parameters of the inverse problem. Observing that these limitations can be due to the proximal algorithm in use, we study a relaxed version of the PGD algorithm for minimizing the sum of a convex function and a weakly convex one. When plugged with a relaxed proximal denoiser, we show that the proposed PnP-$\alpha$PGD algorithm converges for a wider range of regularization parameters, thus allowing more accurate image restoration.

Mumford-Shah functionals on graphs and their asymptotics

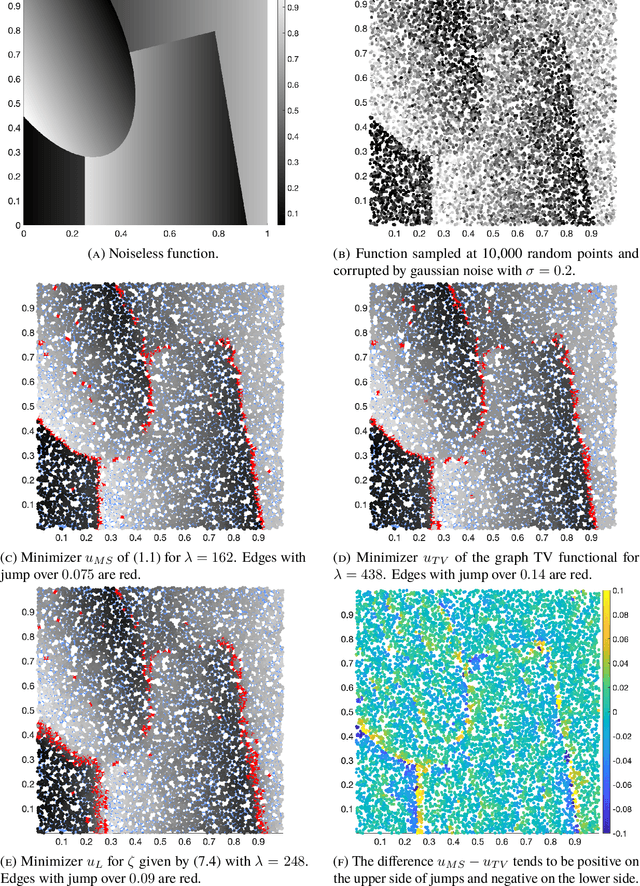
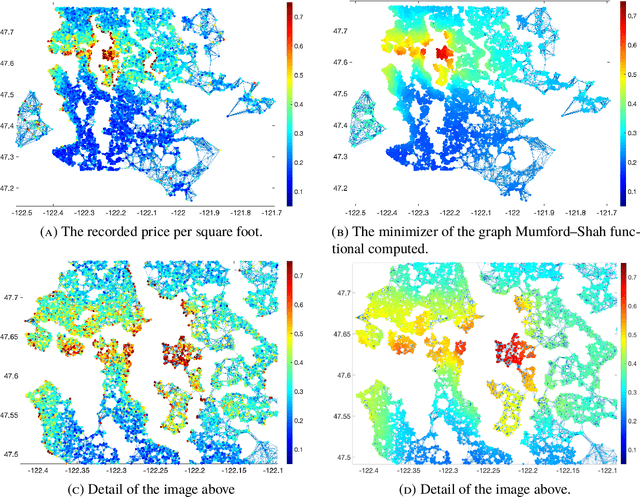
We consider adaptations of the Mumford-Shah functional to graphs. These are based on discretizations of nonlocal approximations to the Mumford-Shah functional. Motivated by applications in machine learning we study the random geometric graphs associated to random samples of a measure. We establish the conditions on the graph constructions under which the minimizers of graph Mumford-Shah functionals converge to a minimizer of a continuum Mumford-Shah functional. Furthermore we explicitly identify the limiting functional. Moreover we describe an efficient algorithm for computing the approximate minimizers of the graph Mumford-Shah functional.

Robust supervised classification and feature selection using a primal-dual method

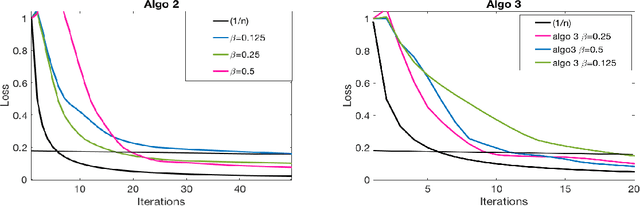
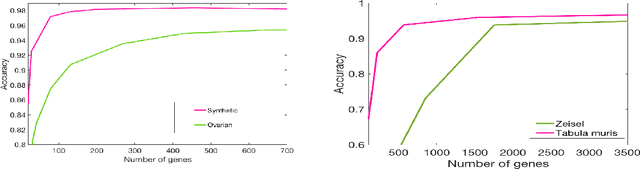
This paper deals with supervised classification and feature selection in high dimensional space. A classical approach is to project data on a low dimensional space and classify by minimizing an appropriate quadratic cost. A strict control on sparsity is moreover obtained by adding an $\ell_1$ constraint, here on the matrix of weights used for projecting the data. Tuning the sparsity bound results in selecting the relevant features for supervised classification. It is well known that using a quadratic cost is not robust to outliers. We cope with this problem by using an $\ell_1$ norm both for the constraint and for the loss function. In this case, the criterion is convex but not gradient Lipschitz anymore. Another second issue is that we optimize simultaneously the projection matrix and the centers used for classification. In this paper, we provide a novel tailored constrained primal-dual method to compute jointly selected features and classifiers. Extending our primal-dual method to other criteria is easy provided that efficient projection (on the dual ball for the loss data term) and prox (for the regularization term) algorithms are available. We illustrate such an extension in the case of a Frobenius norm for the loss term. We provide a convergence proof of our primal-dual method, and demonstrate its effectiveness on three datasets (one synthetic, two from biological data) on which we compare $\ell_1$ and $\ell_2$ costs.

Stochastic Primal-Dual Hybrid Gradient Algorithm with Arbitrary Sampling and Imaging Applications

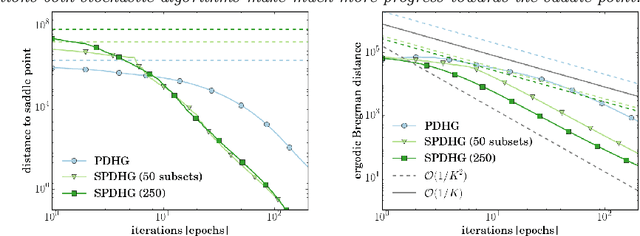
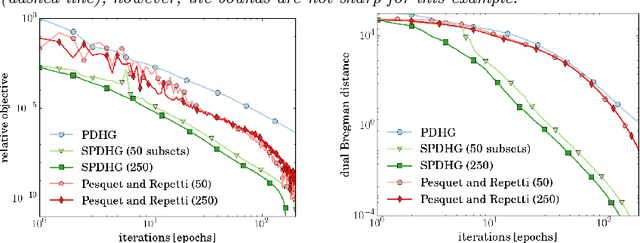
We propose a stochastic extension of the primal-dual hybrid gradient algorithm studied by Chambolle and Pock in 2011 to solve saddle point problems that are separable in the dual variable. The analysis is carried out for general convex-concave saddle point problems and problems that are either partially smooth / strongly convex or fully smooth / strongly convex. We perform the analysis for arbitrary samplings of dual variables, and obtain known deterministic results as a special case. Several variants of our stochastic method significantly outperform the deterministic variant on a variety of imaging tasks.

Total Variation Minimization and Graph Cuts for Moving Objects Segmentation

In this paper, we are interested in the application to video segmentation of the discrete shape optimization problem involving the shape weighted perimeter and an additional term depending on a parameter. Based on recent works and in particular the one of Darbon and Sigelle, we justify the equivalence of the shape optimization problem and a weighted total variation regularization. For solving this problem, we adapt the projection algorithm proposed recently for solving the basic TV regularization problem. Another solution to the shape optimization investigated here is the graph cut technique. Both methods have the advantage to lead to a global minimum. Since we can distinguish moving objects from static elements of a scene by analyzing norm of the optical flow vectors, we choose the optical flow norm as initial data. In order to have the contour as close as possible to an edge in the image, we use a classical edge detector function as the weight of the weighted total variation. This model has been used in one of our former works. We also apply the same methods to a video segmentation model used by Jehan-Besson, Barlaud and Aubert. In this case, only standard perimeter is incorporated in the shape functional. We also propose another way for finding moving objects by using an a contrario detection of objects on the image obtained by solving the Rudin-Osher-Fatemi Total Variation regularization problem.We can notice the segmentation can be associated to a level set in the former methods.