Julie Delon
Robust Barycenters of Persistence Diagrams
Sep 18, 2025
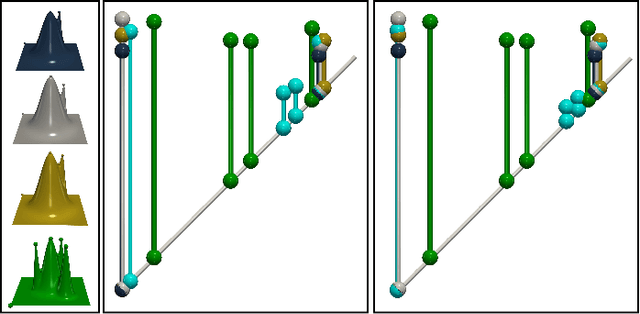
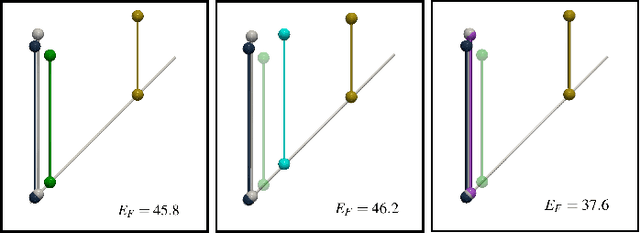
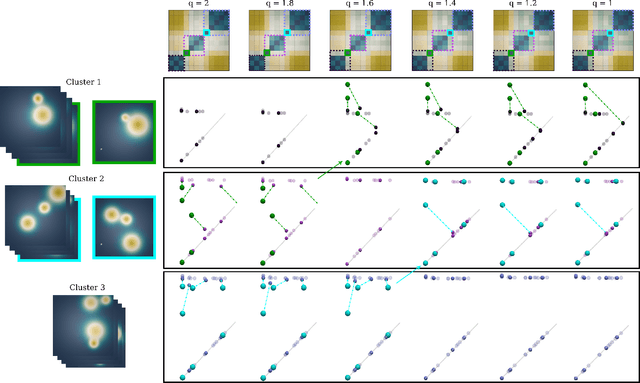
Abstract:This short paper presents a general approach for computing robust Wasserstein barycenters of persistence diagrams. The classical method consists in computing assignment arithmetic means after finding the optimal transport plans between the barycenter and the persistence diagrams. However, this procedure only works for the transportation cost related to the $q$-Wasserstein distance $W_q$ when $q=2$. We adapt an alternative fixed-point method to compute a barycenter diagram for generic transportation costs ($q > 1$), in particular those robust to outliers, $q \in (1,2)$. We show the utility of our work in two applications: \emph{(i)} the clustering of persistence diagrams on their metric space and \emph{(ii)} the dictionary encoding of persistence diagrams. In both scenarios, we demonstrate the added robustness to outliers provided by our generalized framework. Our Python implementation is available at this address: https://github.com/Keanu-Sisouk/RobustBarycenter .
On the Relation between Rectified Flows and Optimal Transport
May 26, 2025Abstract:This paper investigates the connections between rectified flows, flow matching, and optimal transport. Flow matching is a recent approach to learning generative models by estimating velocity fields that guide transformations from a source to a target distribution. Rectified flow matching aims to straighten the learned transport paths, yielding more direct flows between distributions. Our first contribution is a set of invariance properties of rectified flows and explicit velocity fields. In addition, we also provide explicit constructions and analysis in the Gaussian (not necessarily independent) and Gaussian mixture settings and study the relation to optimal transport. Our second contribution addresses recent claims suggesting that rectified flows, when constrained such that the learned velocity field is a gradient, can yield (asymptotically) solutions to optimal transport problems. We study the existence of solutions for this problem and demonstrate that they only relate to optimal transport under assumptions that are significantly stronger than those previously acknowledged. In particular, we present several counter-examples that invalidate earlier equivalence results in the literature, and we argue that enforcing a gradient constraint on rectified flows is, in general, not a reliable method for computing optimal transport maps.
A User's Guide to Sampling Strategies for Sliced Optimal Transport
Feb 05, 2025Abstract:This paper serves as a user's guide to sampling strategies for sliced optimal transport. We provide reminders and additional regularity results on the Sliced Wasserstein distance. We detail the construction methods, generation time complexity, theoretical guarantees, and conditions for each strategy. Additionally, we provide insights into their suitability for sliced optimal transport in theory. Extensive experiments on both simulated and real-world data offer a representative comparison of the strategies, culminating in practical recommendations for their best usage.
Gromov-Wassertein-like Distances in the Gaussian Mixture Models Space
Oct 17, 2023
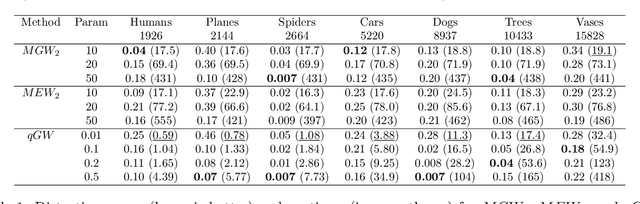
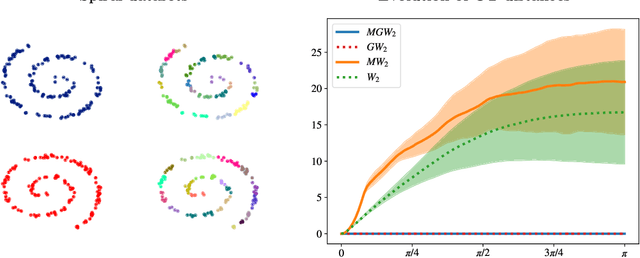
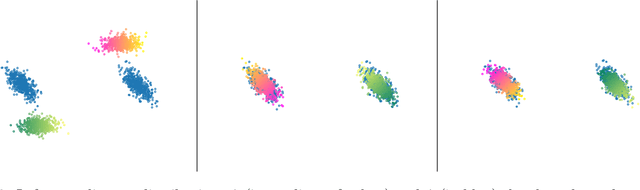
Abstract:In this paper, we introduce two Gromov-Wasserstein-type distances on the set of Gaussian mixture models. The first one takes the form of a Gromov-Wasserstein distance between two discrete distributionson the space of Gaussian measures. This distance can be used as an alternative to Gromov-Wasserstein for applications which only require to evaluate how far the distributions are from each other but does not allow to derive directly an optimal transportation plan between clouds of points. To design a way to define such a transportation plan, we introduce another distance between measures living in incomparable spaces that turns out to be closely related to Gromov-Wasserstein. When restricting the set of admissible transportation couplings to be themselves Gaussian mixture models in this latter, this defines another distance between Gaussian mixture models that can be used as another alternative to Gromov-Wasserstein and which allows to derive an optimal assignment between points. Finally, we design a transportation plan associated with the first distance by analogy with the second, and we illustrate their practical uses on medium-to-large scale problems such as shape matching and hyperspectral image color transfer.
Properties of Discrete Sliced Wasserstein Losses
Jul 19, 2023Abstract:The Sliced Wasserstein (SW) distance has become a popular alternative to the Wasserstein distance for comparing probability measures. Widespread applications include image processing, domain adaptation and generative modelling, where it is common to optimise some parameters in order to minimise SW, which serves as a loss function between discrete probability measures (since measures admitting densities are numerically unattainable). All these optimisation problems bear the same sub-problem, which is minimising the Sliced Wasserstein energy. In this paper we study the properties of $\mathcal{E}: Y \longmapsto \mathrm{SW}_2^2(\gamma_Y, \gamma_Z)$, i.e. the SW distance between two uniform discrete measures with the same amount of points as a function of the support $Y \in \mathbb{R}^{n \times d}$ of one of the measures. We investigate the regularity and optimisation properties of this energy, as well as its Monte-Carlo approximation $\mathcal{E}_p$ (estimating the expectation in SW using only $p$ samples) and show convergence results on the critical points of $\mathcal{E}_p$ to those of $\mathcal{E}$, as well as an almost-sure uniform convergence. Finally, we show that in a certain sense, Stochastic Gradient Descent methods minimising $\mathcal{E}$ and $\mathcal{E}_p$ converge towards (Clarke) critical points of these energies.
Wasserstein Dictionaries of Persistence Diagrams
Apr 28, 2023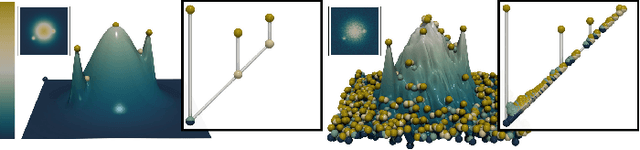
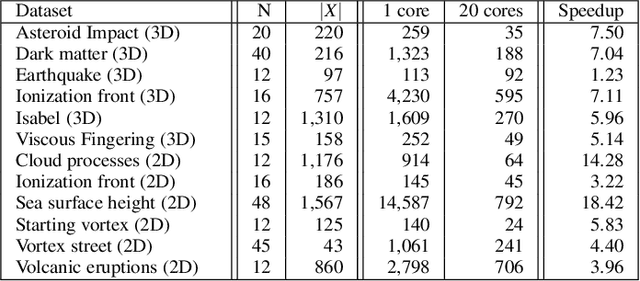
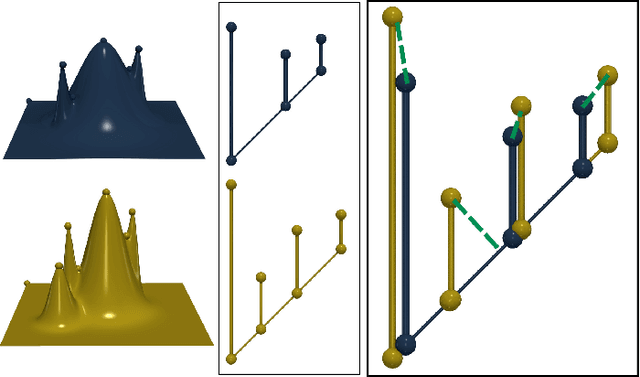
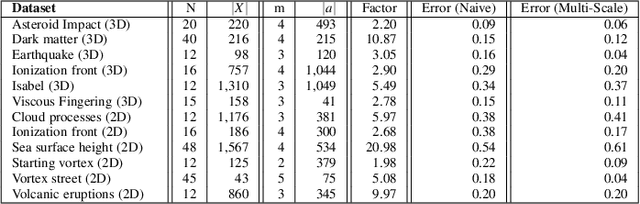
Abstract:This paper presents a computational framework for the concise encoding of an ensemble of persistence diagrams, in the form of weighted Wasserstein barycenters [99], [101] of a dictionary of atom diagrams. We introduce a multi-scale gradient descent approach for the efficient resolution of the corresponding minimization problem, which interleaves the optimization of the barycenter weights with the optimization of the atom diagrams. Our approach leverages the analytic expressions for the gradient of both sub-problems to ensure fast iterations and it additionally exploits shared-memory parallelism. Extensive experiments on public ensembles demonstrate the efficiency of our approach, with Wasserstein dictionary computations in the orders of minutes for the largest examples. We show the utility of our contributions in two applications. First, we apply Wassserstein dictionaries to data reduction and reliably compress persistence diagrams by concisely representing them with their weights in the dictionary. Second, we present a dimensionality reduction framework based on a Wasserstein dictionary defined with a small number of atoms (typically three) and encode the dictionary as a low dimensional simplex embedded in a visual space (typically in 2D). In both applications, quantitative experiments assess the relevance of our framework. Finally, we provide a C++ implementation that can be used to reproduce our results.
Video Restoration with a Deep Plug-and-Play Prior
Sep 15, 2022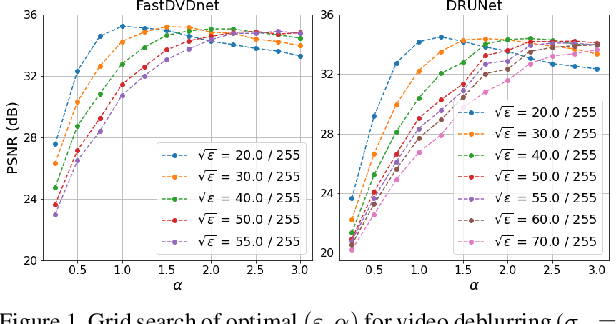

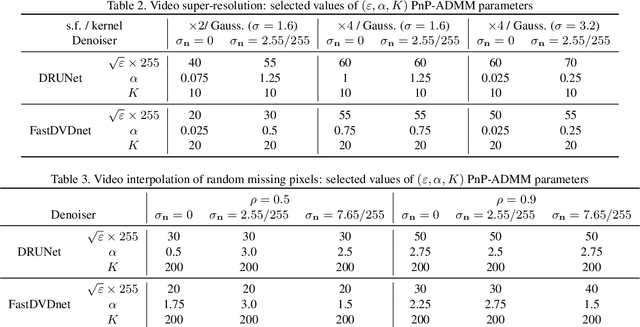
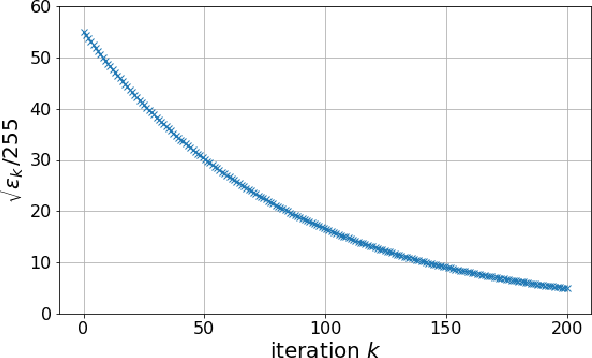
Abstract:This paper presents a novel method for restoring digital videos via a Deep Plug-and-Play (PnP) approach. Under a Bayesian formalism, the method consists in using a deep convolutional denoising network in place of the proximal operator of the prior in an alternating optimization scheme. We distinguish ourselves from prior PnP work by directly applying that method to restore a digital video from a degraded video observation. This way, a network trained once for denoising can be repurposed for other video restoration tasks. Our experiments in video deblurring, super-resolution, and interpolation of random missing pixels all show a clear benefit to using a network specifically designed for video denoising, as it yields better restoration performance and better temporal stability than a single image network with similar denoising performance using the same PnP formulation. Moreover, our method compares favorably to applying a different state-of-the-art PnP scheme separately on each frame of the sequence. This opens new perspectives in the field of video restoration.
Can Push-forward Generative Models Fit Multimodal Distributions?
Jun 29, 2022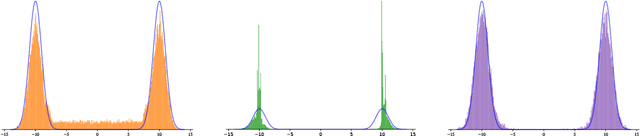
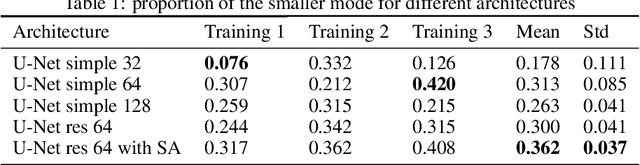
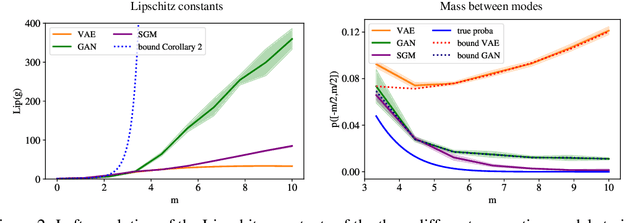

Abstract:Many generative models synthesize data by transforming a standard Gaussian random variable using a deterministic neural network. Among these models are the Variational Autoencoders and the Generative Adversarial Networks. In this work, we call them "push-forward" models and study their expressivity. We show that the Lipschitz constant of these generative networks has to be large in order to fit multimodal distributions. More precisely, we show that the total variation distance and the Kullback-Leibler divergence between the generated and the data distribution are bounded from below by a constant depending on the mode separation and the Lipschitz constant. Since constraining the Lipschitz constants of neural networks is a common way to stabilize generative models, there is a provable trade-off between the ability of push-forward models to approximate multimodal distributions and the stability of their training. We validate our findings on one-dimensional and image datasets and empirically show that generative models consisting of stacked networks with stochastic input at each step, such as diffusion models do not suffer of such limitations.
On Maximum-a-Posteriori estimation with Plug & Play priors and stochastic gradient descent
Jan 16, 2022Abstract:Bayesian methods to solve imaging inverse problems usually combine an explicit data likelihood function with a prior distribution that explicitly models expected properties of the solution. Many kinds of priors have been explored in the literature, from simple ones expressing local properties to more involved ones exploiting image redundancy at a non-local scale. In a departure from explicit modelling, several recent works have proposed and studied the use of implicit priors defined by an image denoising algorithm. This approach, commonly known as Plug & Play (PnP) regularisation, can deliver remarkably accurate results, particularly when combined with state-of-the-art denoisers based on convolutional neural networks. However, the theoretical analysis of PnP Bayesian models and algorithms is difficult and works on the topic often rely on unrealistic assumptions on the properties of the image denoiser. This papers studies maximum-a-posteriori (MAP) estimation for Bayesian models with PnP priors. We first consider questions related to existence, stability and well-posedness, and then present a convergence proof for MAP computation by PnP stochastic gradient descent (PnP-SGD) under realistic assumptions on the denoiser used. We report a range of imaging experiments demonstrating PnP-SGD as well as comparisons with other PnP schemes.
An Analysis and Implementation of the HDR+ Burst Denoising Method
Oct 18, 2021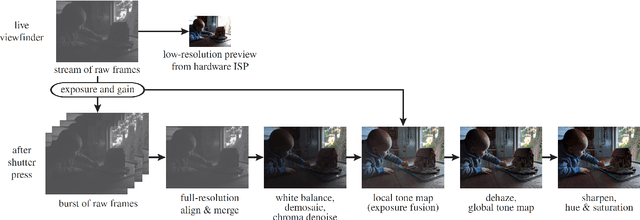


Abstract:HDR+ is an image processing pipeline presented by Google in 2016. At its core lies a denoising algorithm that uses a burst of raw images to produce a single higher quality image. Since it is designed as a versatile solution for smartphone cameras, it does not necessarily aim for the maximization of standard denoising metrics, but rather for the production of natural, visually pleasing images. In this article, we specifically discuss and analyze the HDR+ burst denoising algorithm architecture and the impact of its various parameters. With this publication, we provide an open source Python implementation of the algorithm, along with an interactive demo.
* 28 pages, 15 figures, published at https://doi.org/10.5201/ipol.2021.336, code on https://github.com/amonod/hdrplus-python
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge