BN-SCAFFOLD: controlling the drift of Batch Normalization statistics in Federated Learning

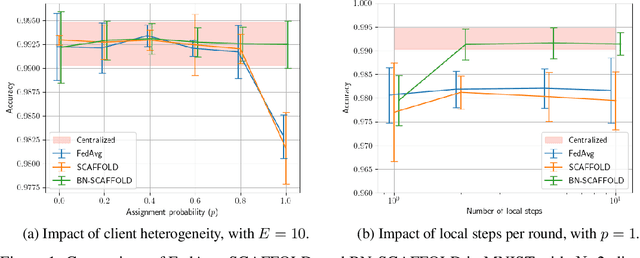
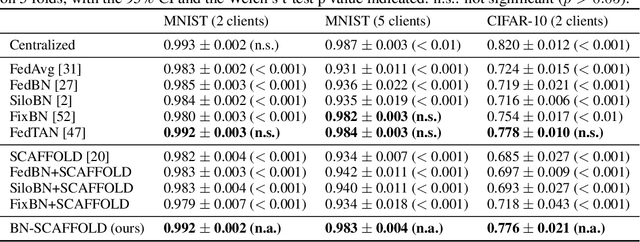
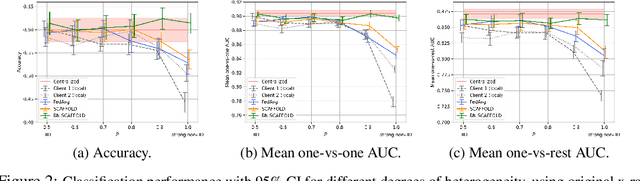
Federated Learning (FL) is gaining traction as a learning paradigm for training Machine Learning (ML) models in a decentralized way. Batch Normalization (BN) is ubiquitous in Deep Neural Networks (DNN), as it improves convergence and generalization. However, BN has been reported to hinder performance of DNNs in heterogeneous FL. Recently, the FedTAN algorithm has been proposed to mitigate the effect of heterogeneity on BN, by aggregating BN statistics and gradients from all the clients. However, it has a high communication cost, that increases linearly with the depth of the DNN. SCAFFOLD is a variance reduction algorithm, that estimates and corrects the client drift in a communication-efficient manner. Despite its promising results in heterogeneous FL settings, it has been reported to underperform for models with BN. In this work, we seek to revive SCAFFOLD, and more generally variance reduction, as an efficient way of training DNN with BN in heterogeneous FL. We introduce a unified theoretical framework for analyzing the convergence of variance reduction algorithms in the BN-DNN setting, inspired of by the work of Wang et al. 2023, and show that SCAFFOLD is unable to remove the bias introduced by BN. We thus propose the BN-SCAFFOLD algorithm, which extends the client drift correction of SCAFFOLD to BN statistics. We prove convergence using the aforementioned framework and validate the theoretical results with experiments on MNIST and CIFAR-10. BN-SCAFFOLD equals the performance of FedTAN, without its high communication cost, outperforming Federated Averaging (FedAvg), SCAFFOLD, and other FL algorithms designed to mitigate BN heterogeneity.

Gromov-Wassertein-like Distances in the Gaussian Mixture Models Space

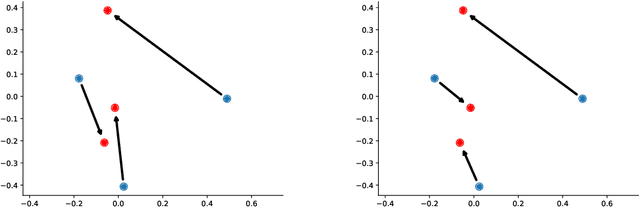
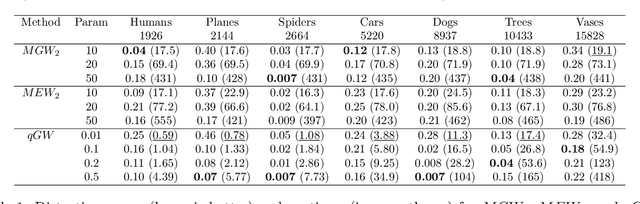
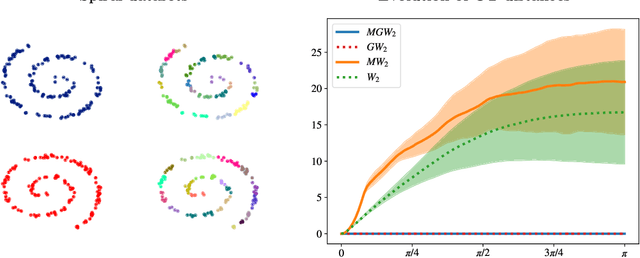
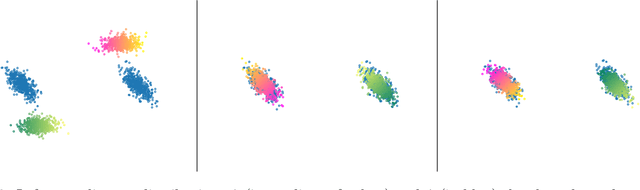
In this paper, we introduce two Gromov-Wasserstein-type distances on the set of Gaussian mixture models. The first one takes the form of a Gromov-Wasserstein distance between two discrete distributionson the space of Gaussian measures. This distance can be used as an alternative to Gromov-Wasserstein for applications which only require to evaluate how far the distributions are from each other but does not allow to derive directly an optimal transportation plan between clouds of points. To design a way to define such a transportation plan, we introduce another distance between measures living in incomparable spaces that turns out to be closely related to Gromov-Wasserstein. When restricting the set of admissible transportation couplings to be themselves Gaussian mixture models in this latter, this defines another distance between Gaussian mixture models that can be used as another alternative to Gromov-Wasserstein and which allows to derive an optimal assignment between points. Finally, we design a transportation plan associated with the first distance by analogy with the second, and we illustrate their practical uses on medium-to-large scale problems such as shape matching and hyperspectral image color transfer.

Can Push-forward Generative Models Fit Multimodal Distributions?

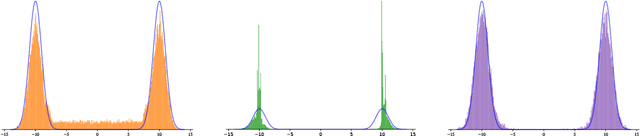
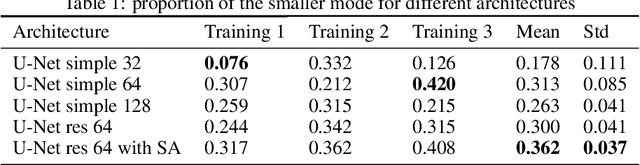
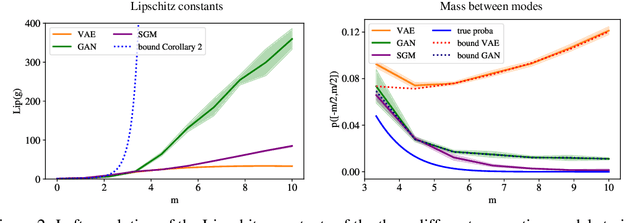
Many generative models synthesize data by transforming a standard Gaussian random variable using a deterministic neural network. Among these models are the Variational Autoencoders and the Generative Adversarial Networks. In this work, we call them "push-forward" models and study their expressivity. We show that the Lipschitz constant of these generative networks has to be large in order to fit multimodal distributions. More precisely, we show that the total variation distance and the Kullback-Leibler divergence between the generated and the data distribution are bounded from below by a constant depending on the mode separation and the Lipschitz constant. Since constraining the Lipschitz constants of neural networks is a common way to stabilize generative models, there is a provable trade-off between the ability of push-forward models to approximate multimodal distributions and the stability of their training. We validate our findings on one-dimensional and image datasets and empirically show that generative models consisting of stacked networks with stochastic input at each step, such as diffusion models do not suffer of such limitations.

On quantitative Laplace-type convergence results for some exponential probability measures, with two applications

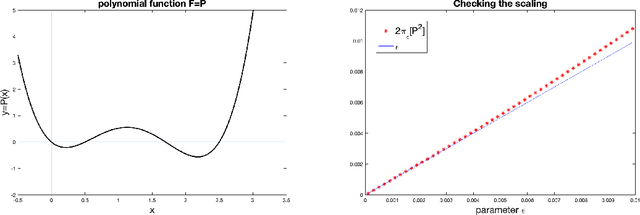
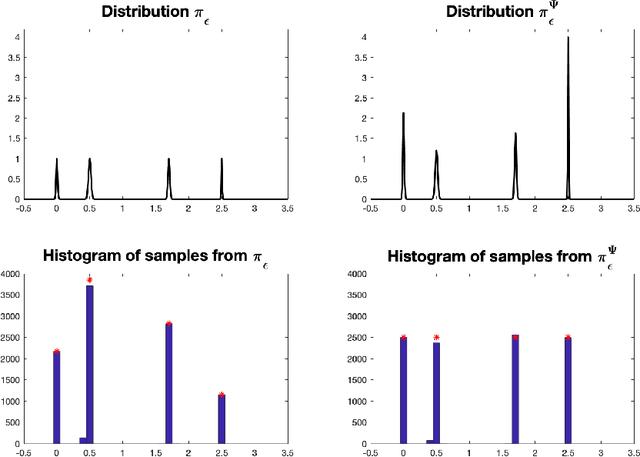
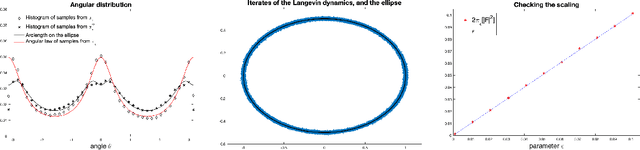
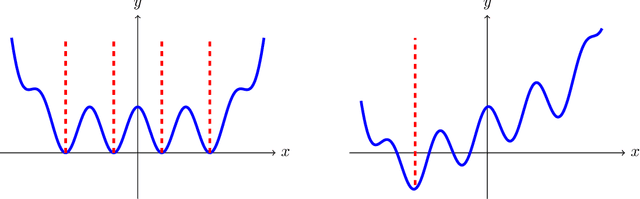
Laplace-type results characterize the limit of sequence of measures $(\pi_\varepsilon)_{\varepsilon >0}$ with density w.r.t the Lebesgue measure $(\mathrm{d} \pi_\varepsilon / \mathrm{d} \mathrm{Leb})(x) \propto \exp[-U(x)/\varepsilon]$ when the temperature $\varepsilon>0$ converges to $0$. If a limiting distribution $\pi_0$ exists, it concentrates on the minimizers of the potential $U$. Classical results require the invertibility of the Hessian of $U$ in order to establish such asymptotics. In this work, we study the particular case of norm-like potentials $U$ and establish quantitative bounds between $\pi_\varepsilon$ and $\pi_0$ w.r.t. the Wasserstein distance of order $1$ under an invertibility condition of a generalized Jacobian. One key element of our proof is the use of geometric measure theory tools such as the coarea formula. We apply our results to the study of maximum entropy models (microcanonical/macrocanonical distributions) and to the convergence of the iterates of the Stochastic Gradient Langevin Dynamics (SGLD) algorithm at low temperatures for non-convex minimization.

Unidentified Floating Object detection in maritime environment using dictionary learning

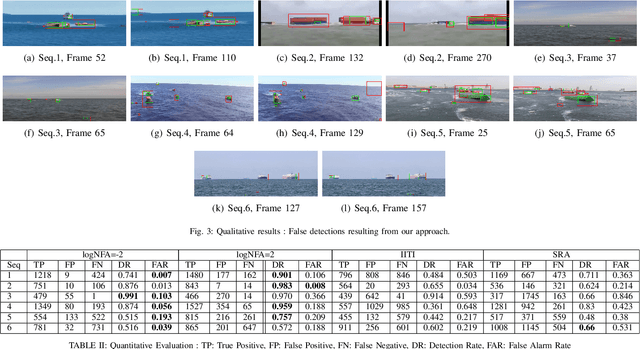
Maritime domain is one of the most challenging scenarios for object detection due to the complexity of the observed scene. In this article, we present a new approach to detect unidentified floating objects in the maritime environment. The proposed approach is capable of detecting floating objects without any prior knowledge of their visual appearance, shape or location. The input image from the video stream is denoised using a visual dictionary learned from a K-SVD algorithm. The denoised image is made of self-similar content. Later, we extract the residual image, which is the difference between the original image and the denoised (self-similar) image. Thus, the residual image contains noise and salient structures (objects). These salient structures can be extracted using an a contrario model. We demonstrate the capabilities of our algorithm by testing it on videos exhibiting varying maritime scenarios.

Exact Sampling of Determinantal Point Processes without Eigendecomposition

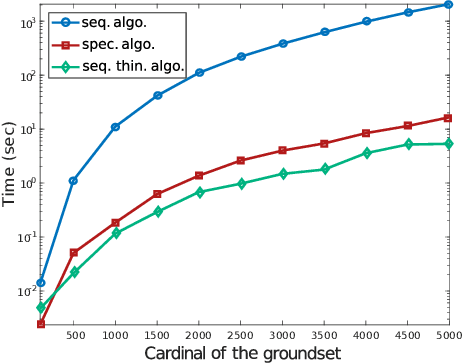
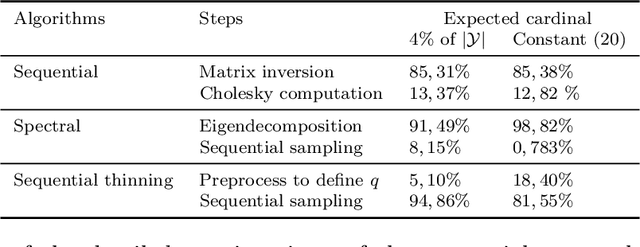
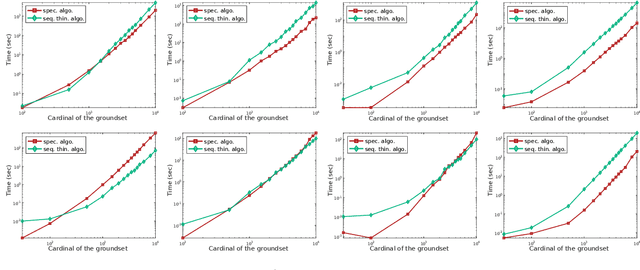
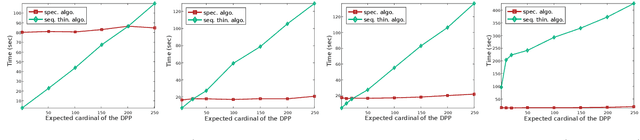
Determinantal point processes (DPPs) enable the modelling of repulsion: they provide diverse sets of points. This repulsion is encoded in a kernel K that we can see as a matrix storing the similarity between points. The usual algorithm to sample DPPs is exact but it uses the spectral decomposition of K, a computation that becomes costly when dealing with a high number of points. Here, we present an alternative exact algorithm that avoids the eigenvalues and the eigenvectors computation and that is, for some applications, faster than the original algorithm.

A survey of exemplar-based texture synthesis

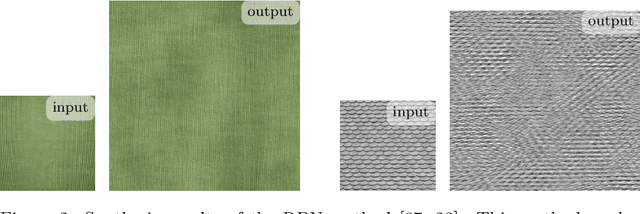
Exemplar-based texture synthesis is the process of generating, from an input sample, new texture images of arbitrary size and which are perceptually equivalent to the sample. The two main approaches are statistics-based methods and patch re-arrangement methods. In the first class, a texture is characterized by a statistical signature; then, a random sampling conditioned to this signature produces genuinely different texture images. The second class boils down to a clever "copy-paste" procedure, which stitches together large regions of the sample. Hybrid methods try to combine ideas from both approaches to avoid their hurdles. The recent approaches using convolutional neural networks fit to this classification, some being statistical and others performing patch re-arrangement in the feature space. They produce impressive synthesis on various kinds of textures. Nevertheless, we found that most real textures are organized at multiple scales, with global structures revealed at coarse scales and highly varying details at finer ones. Thus, when confronted with large natural images of textures the results of state-of-the-art methods degrade rapidly, and the problem of modeling them remains wide open.