Gromov-Wassertein-like Distances in the Gaussian Mixture Models Space

In this paper, we introduce two Gromov-Wasserstein-type distances on the set of Gaussian mixture models. The first one takes the form of a Gromov-Wasserstein distance between two discrete distributionson the space of Gaussian measures. This distance can be used as an alternative to Gromov-Wasserstein for applications which only require to evaluate how far the distributions are from each other but does not allow to derive directly an optimal transportation plan between clouds of points. To design a way to define such a transportation plan, we introduce another distance between measures living in incomparable spaces that turns out to be closely related to Gromov-Wasserstein. When restricting the set of admissible transportation couplings to be themselves Gaussian mixture models in this latter, this defines another distance between Gaussian mixture models that can be used as another alternative to Gromov-Wasserstein and which allows to derive an optimal assignment between points. Finally, we design a transportation plan associated with the first distance by analogy with the second, and we illustrate their practical uses on medium-to-large scale problems such as shape matching and hyperspectral image color transfer.

Can Push-forward Generative Models Fit Multimodal Distributions?

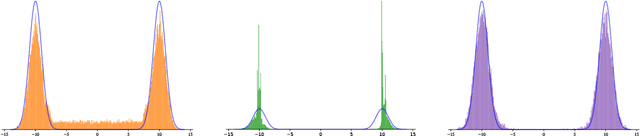
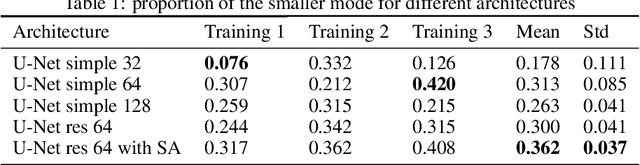
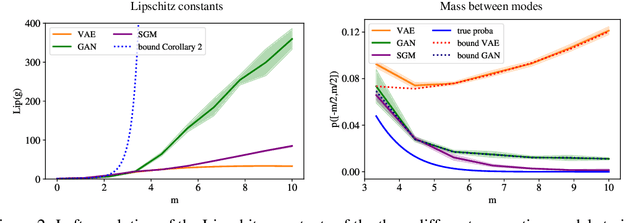
Many generative models synthesize data by transforming a standard Gaussian random variable using a deterministic neural network. Among these models are the Variational Autoencoders and the Generative Adversarial Networks. In this work, we call them "push-forward" models and study their expressivity. We show that the Lipschitz constant of these generative networks has to be large in order to fit multimodal distributions. More precisely, we show that the total variation distance and the Kullback-Leibler divergence between the generated and the data distribution are bounded from below by a constant depending on the mode separation and the Lipschitz constant. Since constraining the Lipschitz constants of neural networks is a common way to stabilize generative models, there is a provable trade-off between the ability of push-forward models to approximate multimodal distributions and the stability of their training. We validate our findings on one-dimensional and image datasets and empirically show that generative models consisting of stacked networks with stochastic input at each step, such as diffusion models do not suffer of such limitations.