Gromov-Wassertein-like Distances in the Gaussian Mixture Models Space
Paper and Code
Oct 17, 2023
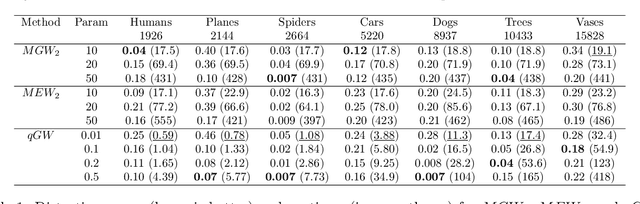
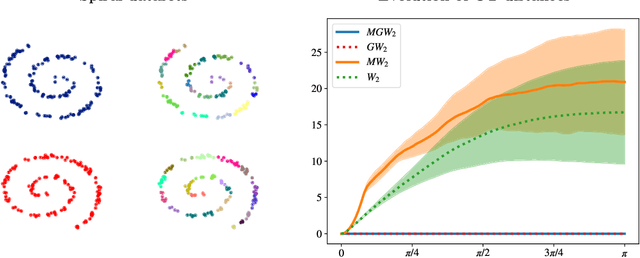
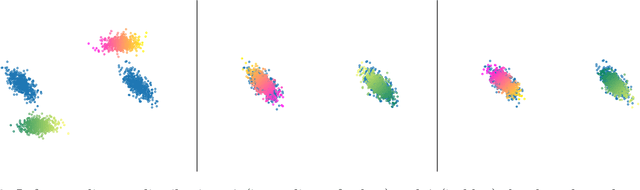
In this paper, we introduce two Gromov-Wasserstein-type distances on the set of Gaussian mixture models. The first one takes the form of a Gromov-Wasserstein distance between two discrete distributionson the space of Gaussian measures. This distance can be used as an alternative to Gromov-Wasserstein for applications which only require to evaluate how far the distributions are from each other but does not allow to derive directly an optimal transportation plan between clouds of points. To design a way to define such a transportation plan, we introduce another distance between measures living in incomparable spaces that turns out to be closely related to Gromov-Wasserstein. When restricting the set of admissible transportation couplings to be themselves Gaussian mixture models in this latter, this defines another distance between Gaussian mixture models that can be used as another alternative to Gromov-Wasserstein and which allows to derive an optimal assignment between points. Finally, we design a transportation plan associated with the first distance by analogy with the second, and we illustrate their practical uses on medium-to-large scale problems such as shape matching and hyperspectral image color transfer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge