Cascaded Transfer: Learning Many Tasks under Budget Constraints

Many-Task Learning refers to the setting where a large number of related tasks need to be learned, the exact relationships between tasks are not known. We introduce the Cascaded Transfer Learning, a novel many-task transfer learning paradigm where information (e.g. model parameters) cascades hierarchically through tasks that are learned by individual models of the same class, while respecting given budget constraints. The cascade is organized as a rooted tree that specifies the order in which tasks are learned and refined. We design a cascaded transfer mechanism deployed over a minimum spanning tree structure that connects the tasks according to a suitable distance measure, and allocates the available training budget along its branches. Experiments on synthetic and real many-task settings show that the resulting method enables more accurate and cost effective adaptation across large task collections compared to alternative approaches.

Multi-Component VAE with Gaussian Markov Random Field

Multi-component datasets with intricate dependencies, like industrial assemblies or multi-modal imaging, challenge current generative modeling techniques. Existing Multi-component Variational AutoEncoders typically rely on simplified aggregation strategies, neglecting critical nuances and consequently compromising structural coherence across generated components. To explicitly address this gap, we introduce the Gaussian Markov Random Field Multi-Component Variational AutoEncoder , a novel generative framework embedding Gaussian Markov Random Fields into both prior and posterior distributions. This design choice explicitly models cross-component relationships, enabling richer representation and faithful reproduction of complex interactions. Empirically, our GMRF MCVAE achieves state-of-the-art performance on a synthetic Copula dataset specifically constructed to evaluate intricate component relationships, demonstrates competitive results on the PolyMNIST benchmark, and significantly enhances structural coherence on the real-world BIKED dataset. Our results indicate that the GMRF MCVAE is especially suited for practical applications demanding robust and realistic modeling of multi-component coherence

Deep Generative Methods and Tire Architecture Design

As deep generative models proliferate across the AI landscape, industrial practitioners still face critical yet unanswered questions about which deep generative models best suit complex manufacturing design tasks. This work addresses this question through a complete study of five representative models (Variational Autoencoder, Generative Adversarial Network, multimodal Variational Autoencoder, Denoising Diffusion Probabilistic Model, and Multinomial Diffusion Model) on industrial tire architecture generation. Our evaluation spans three key industrial scenarios: (i) unconditional generation of complete multi-component designs, (ii) component-conditioned generation (reconstructing architectures from partial observations), and (iii) dimension-constrained generation (creating designs that satisfy specific dimensional requirements). To enable discrete diffusion models to handle conditional scenarios, we introduce categorical inpainting, a mask-aware reverse diffusion process that preserves known labels without requiring additional training. Our evaluation employs geometry-aware metrics specifically calibrated for industrial requirements, quantifying spatial coherence, component interaction, structural connectivity, and perceptual fidelity. Our findings reveal that diffusion models achieve the strongest overall performance; a masking-trained VAE nonetheless outperforms the multimodal variant MMVAE\textsuperscript{+} on nearly all component-conditioned metrics, and within the diffusion family MDM leads in-distribution whereas DDPM generalises better to out-of-distribution dimensional constraints.

OneBatchPAM: A Fast and Frugal K-Medoids Algorithm

This paper proposes a novel k-medoids approximation algorithm to handle large-scale datasets with reasonable computational time and memory complexity. We develop a local-search algorithm that iteratively improves the medoid selection based on the estimation of the k-medoids objective. A single batch of size m << n provides the estimation, which reduces the required memory size and the number of pairwise dissimilarities computations to O(mn), instead of O(n^2) compared to most k-medoids baselines. We obtain theoretical results highlighting that a batch of size m = O(log(n)) is sufficient to guarantee, with strong probability, the same performance as the original local-search algorithm. Multiple experiments conducted on real datasets of various sizes and dimensions show that our algorithm provides similar performances as state-of-the-art methods such as FasterPAM and BanditPAM++ with a drastically reduced running time.

BN-SCAFFOLD: controlling the drift of Batch Normalization statistics in Federated Learning

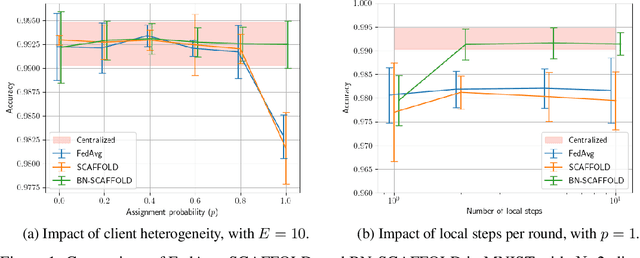
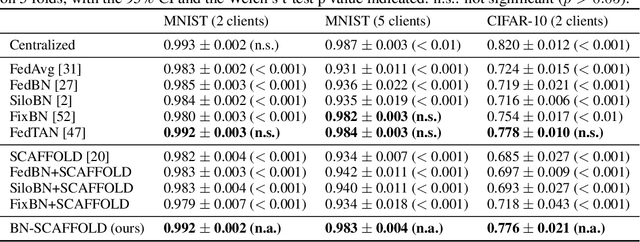
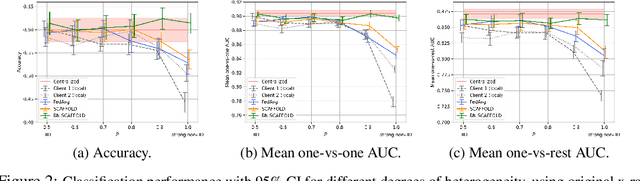
Federated Learning (FL) is gaining traction as a learning paradigm for training Machine Learning (ML) models in a decentralized way. Batch Normalization (BN) is ubiquitous in Deep Neural Networks (DNN), as it improves convergence and generalization. However, BN has been reported to hinder performance of DNNs in heterogeneous FL. Recently, the FedTAN algorithm has been proposed to mitigate the effect of heterogeneity on BN, by aggregating BN statistics and gradients from all the clients. However, it has a high communication cost, that increases linearly with the depth of the DNN. SCAFFOLD is a variance reduction algorithm, that estimates and corrects the client drift in a communication-efficient manner. Despite its promising results in heterogeneous FL settings, it has been reported to underperform for models with BN. In this work, we seek to revive SCAFFOLD, and more generally variance reduction, as an efficient way of training DNN with BN in heterogeneous FL. We introduce a unified theoretical framework for analyzing the convergence of variance reduction algorithms in the BN-DNN setting, inspired of by the work of Wang et al. 2023, and show that SCAFFOLD is unable to remove the bias introduced by BN. We thus propose the BN-SCAFFOLD algorithm, which extends the client drift correction of SCAFFOLD to BN statistics. We prove convergence using the aforementioned framework and validate the theoretical results with experiments on MNIST and CIFAR-10. BN-SCAFFOLD equals the performance of FedTAN, without its high communication cost, outperforming Federated Averaging (FedAvg), SCAFFOLD, and other FL algorithms designed to mitigate BN heterogeneity.

A Markov Random Field Multi-Modal Variational AutoEncoder

Recent advancements in multimodal Variational AutoEncoders (VAEs) have highlighted their potential for modeling complex data from multiple modalities. However, many existing approaches use relatively straightforward aggregating schemes that may not fully capture the complex dynamics present between different modalities. This work introduces a novel multimodal VAE that incorporates a Markov Random Field (MRF) into both the prior and posterior distributions. This integration aims to capture complex intermodal interactions more effectively. Unlike previous models, our approach is specifically designed to model and leverage the intricacies of these relationships, enabling a more faithful representation of multimodal data. Our experiments demonstrate that our model performs competitively on the standard PolyMNIST dataset and shows superior performance in managing complex intermodal dependencies in a specially designed synthetic dataset, intended to test intricate relationships.

Geometry-aware framework for deep energy method: an application to structural mechanics with hyperelastic materials

Physics-Informed Neural Networks (PINNs) have gained considerable interest in diverse engineering domains thanks to their capacity to integrate physical laws into deep learning models. Recently, geometry-aware PINN-based approaches that employ the strong form of underlying physical system equations have been developed with the aim of integrating geometric information into PINNs. Despite ongoing research, the assessment of PINNs in problems with various geometries remains an active area of investigation. In this work, we introduce a novel physics-informed framework named the Geometry-Aware Deep Energy Method (GADEM) for solving structural mechanics problems on different geometries. As the weak form of the physical system equation (or the energy-based approach) has demonstrated clear advantages compared to the strong form for solving solid mechanics problems, GADEM employs the weak form and aims to infer the solution on multiple shapes of geometries. Integrating a geometry-aware framework into an energy-based method results in an effective physics-informed deep learning model in terms of accuracy and computational cost. Different ways to represent the geometric information and to encode the geometric latent vectors are investigated in this work. We introduce a loss function of GADEM which is minimized based on the potential energy of all considered geometries. An adaptive learning method is also employed for the sampling of collocation points to enhance the performance of GADEM. We present some applications of GADEM to solve solid mechanics problems, including a loading simulation of a toy tire involving contact mechanics and large deformation hyperelasticity. The numerical results of this work demonstrate the remarkable capability of GADEM to infer the solution on various and new shapes of geometries using only one trained model.

Conformal Approach To Gaussian Process Surrogate Evaluation With Coverage Guarantees

Gaussian processes (GPs) are a Bayesian machine learning approach widely used to construct surrogate models for the uncertainty quantification of computer simulation codes in industrial applications. It provides both a mean predictor and an estimate of the posterior prediction variance, the latter being used to produce Bayesian credibility intervals. Interpreting these intervals relies on the Gaussianity of the simulation model as well as the well-specification of the priors which are not always appropriate. We propose to address this issue with the help of conformal prediction. In the present work, a method for building adaptive cross-conformal prediction intervals is proposed by weighting the non-conformity score with the posterior standard deviation of the GP. The resulting conformal prediction intervals exhibit a level of adaptivity akin to Bayesian credibility sets and display a significant correlation with the surrogate model local approximation error, while being free from the underlying model assumptions and having frequentist coverage guarantees. These estimators can thus be used for evaluating the quality of a GP surrogate model and can assist a decision-maker in the choice of the best prior for the specific application of the GP. The performance of the method is illustrated through a panel of numerical examples based on various reference databases. Moreover, the potential applicability of the method is demonstrated in the context of surrogate modeling of an expensive-to-evaluate simulator of the clogging phenomenon in steam generators of nuclear reactors.

Maximum Weight Entropy

This paper deals with uncertainty quantification and out-of-distribution detection in deep learning using Bayesian and ensemble methods. It proposes a practical solution to the lack of prediction diversity observed recently for standard approaches when used out-of-distribution (Ovadia et al., 2019; Liu et al., 2021). Considering that this issue is mainly related to a lack of weight diversity, we claim that standard methods sample in "over-restricted" regions of the weight space due to the use of "over-regularization" processes, such as weight decay and zero-mean centered Gaussian priors. We propose to solve the problem by adopting the maximum entropy principle for the weight distribution, with the underlying idea to maximize the weight diversity. Under this paradigm, the epistemic uncertainty is described by the weight distribution of maximal entropy that produces neural networks "consistent" with the training observations. Considering stochastic neural networks, a practical optimization is derived to build such a distribution, defined as a trade-off between the average empirical risk and the weight distribution entropy. We develop a novel weight parameterization for the stochastic model, based on the singular value decomposition of the neural network's hidden representations, which enables a large increase of the weight entropy for a small empirical risk penalization. We provide both theoretical and numerical results to assess the efficiency of the approach. In particular, the proposed algorithm appears in the top three best methods in all configurations of an extensive out-of-distribution detection benchmark including more than thirty competitors.

A Meta-Generation framework for Industrial System Generation

Generative design is an increasingly important tool in the industrial world. It allows the designers and engineers to easily explore vast ranges of design options, providing a cheaper and faster alternative to the trial and failure approaches. Thanks to the flexibility they offer, Deep Generative Models are gaining popularity amongst Generative Design technologies. However, developing and evaluating these models can be challenging. The field lacks accessible benchmarks, in order to evaluate and compare objectively different Deep Generative Models architectures. Moreover, vanilla Deep Generative Models appear to be unable to accurately generate multi-components industrial systems that are controlled by latent design constraints. To address these challenges, we propose an industry-inspired use case that incorporates actual industrial system characteristics. This use case can be quickly generated and used as a benchmark. We propose a Meta-VAE capable of producing multi-component industrial systems and showcase its application on the proposed use case.