OneBatchPAM: A Fast and Frugal K-Medoids Algorithm

This paper proposes a novel k-medoids approximation algorithm to handle large-scale datasets with reasonable computational time and memory complexity. We develop a local-search algorithm that iteratively improves the medoid selection based on the estimation of the k-medoids objective. A single batch of size m << n provides the estimation, which reduces the required memory size and the number of pairwise dissimilarities computations to O(mn), instead of O(n^2) compared to most k-medoids baselines. We obtain theoretical results highlighting that a batch of size m = O(log(n)) is sufficient to guarantee, with strong probability, the same performance as the original local-search algorithm. Multiple experiments conducted on real datasets of various sizes and dimensions show that our algorithm provides similar performances as state-of-the-art methods such as FasterPAM and BanditPAM++ with a drastically reduced running time.

A Pre-Trained Graph-Based Model for Adaptive Sequencing of Educational Documents

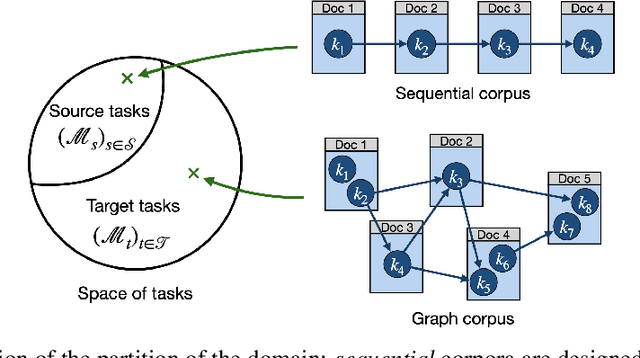
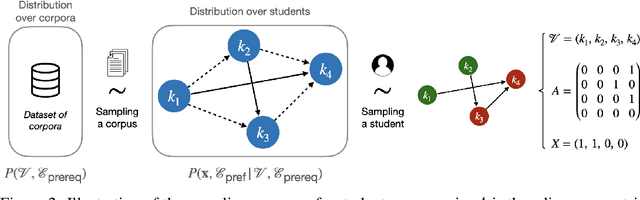
Massive Open Online Courses (MOOCs) have greatly contributed to making education more accessible. However, many MOOCs maintain a rigid, one-size-fits-all structure that fails to address the diverse needs and backgrounds of individual learners. Learning path personalization aims to address this limitation, by tailoring sequences of educational content to optimize individual student learning outcomes. Existing approaches, however, often require either massive student interaction data or extensive expert annotation, limiting their broad application. In this study, we introduce a novel data-efficient framework for learning path personalization that operates without expert annotation. Our method employs a flexible recommender system pre-trained with reinforcement learning on a dataset of raw course materials. Through experiments on semi-synthetic data, we show that this pre-training stage substantially improves data-efficiency in a range of adaptive learning scenarios featuring new educational materials. This opens up new perspectives for the design of foundation models for adaptive learning.

Stein Boltzmann Sampling: A Variational Approach for Global Optimization

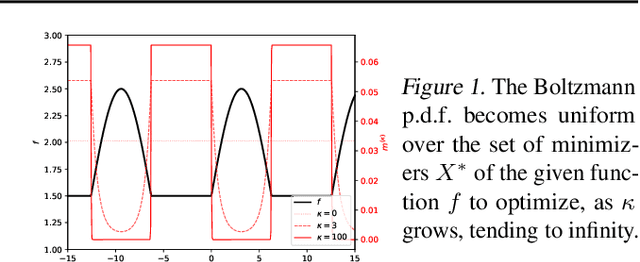
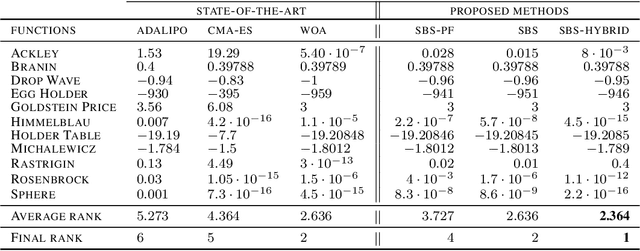
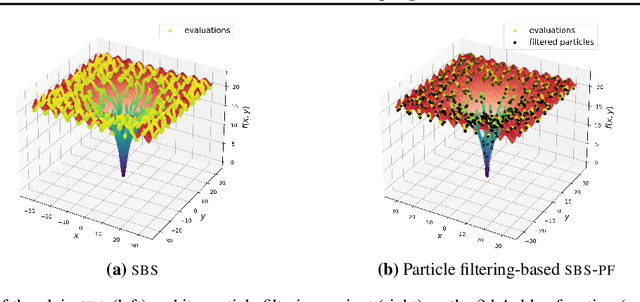
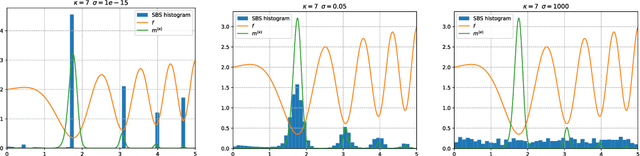
In this paper, we introduce a new flow-based method for global optimization of Lipschitz functions, called Stein Boltzmann Sampling (SBS). Our method samples from the Boltzmann distribution that becomes asymptotically uniform over the set of the minimizers of the function to be optimized. Candidate solutions are sampled via the \emph{Stein Variational Gradient Descent} algorithm. We prove the asymptotic convergence of our method, introduce two SBS variants, and provide a detailed comparison with several state-of-the-art global optimization algorithms on various benchmark functions. The design of our method, the theoretical results, and our experiments, suggest that SBS is particularly well-suited to be used as a continuation of efficient global optimization methods as it can produce better solutions while making a good use of the budget.

Collaborative non-parametric two-sample testing

This paper addresses the multiple two-sample test problem in a graph-structured setting, which is a common scenario in fields such as Spatial Statistics and Neuroscience. Each node $v$ in fixed graph deals with a two-sample testing problem between two node-specific probability density functions (pdfs), $p_v$ and $q_v$. The goal is to identify nodes where the null hypothesis $p_v = q_v$ should be rejected, under the assumption that connected nodes would yield similar test outcomes. We propose the non-parametric collaborative two-sample testing (CTST) framework that efficiently leverages the graph structure and minimizes the assumptions over $p_v$ and $q_v$. Our methodology integrates elements from f-divergence estimation, Kernel Methods, and Multitask Learning. We use synthetic experiments and a real sensor network detecting seismic activity to demonstrate that CTST outperforms state-of-the-art non-parametric statistical tests that apply at each node independently, hence disregard the geometry of the problem.

Online non-parametric likelihood-ratio estimation by Pearson-divergence functional minimization

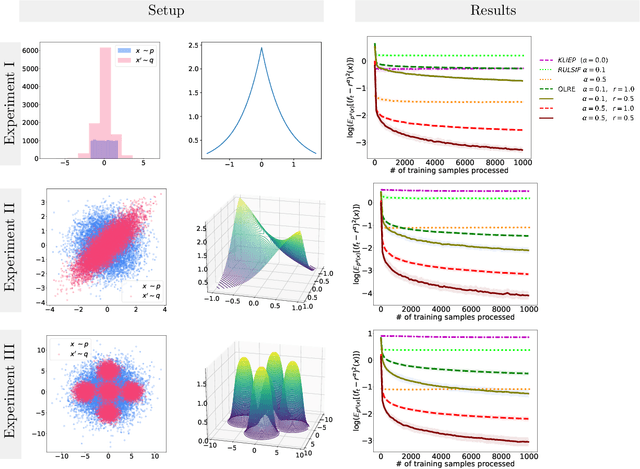
Quantifying the difference between two probability density functions, $p$ and $q$, using available data, is a fundamental problem in Statistics and Machine Learning. A usual approach for addressing this problem is the likelihood-ratio estimation (LRE) between $p$ and $q$, which -- to our best knowledge -- has been investigated mainly for the offline case. This paper contributes by introducing a new framework for online non-parametric LRE (OLRE) for the setting where pairs of iid observations $(x_t \sim p, x'_t \sim q)$ are observed over time. The non-parametric nature of our approach has the advantage of being agnostic to the forms of $p$ and $q$. Moreover, we capitalize on the recent advances in Kernel Methods and functional minimization to develop an estimator that can be efficiently updated online. We provide theoretical guarantees for the performance of the OLRE method along with empirical validation in synthetic experiments.

A framework for paired-sample hypothesis testing for high-dimensional data

The standard paired-sample testing approach in the multidimensional setting applies multiple univariate tests on the individual features, followed by p-value adjustments. Such an approach suffers when the data carry numerous features. A number of studies have shown that classification accuracy can be seen as a proxy for two-sample testing. However, neither theoretical foundations nor practical recipes have been proposed so far on how this strategy could be extended to multidimensional paired-sample testing. In this work, we put forward the idea that scoring functions can be produced by the decision rules defined by the perpendicular bisecting hyperplanes of the line segments connecting each pair of instances. Then, the optimal scoring function can be obtained by the pseudomedian of those rules, which we estimate by extending naturally the Hodges-Lehmann estimator. We accordingly propose a framework of a two-step testing procedure. First, we estimate the bisecting hyperplanes for each pair of instances and an aggregated rule derived through the Hodges-Lehmann estimator. The paired samples are scored by this aggregated rule to produce a unidimensional representation. Second, we perform a Wilcoxon signed-rank test on the obtained representation. Our experiments indicate that our approach has substantial performance gains in testing accuracy compared to the traditional multivariate and multiple testing, while at the same time estimates each feature's contribution to the final result.

Maximum Weight Entropy

This paper deals with uncertainty quantification and out-of-distribution detection in deep learning using Bayesian and ensemble methods. It proposes a practical solution to the lack of prediction diversity observed recently for standard approaches when used out-of-distribution (Ovadia et al., 2019; Liu et al., 2021). Considering that this issue is mainly related to a lack of weight diversity, we claim that standard methods sample in "over-restricted" regions of the weight space due to the use of "over-regularization" processes, such as weight decay and zero-mean centered Gaussian priors. We propose to solve the problem by adopting the maximum entropy principle for the weight distribution, with the underlying idea to maximize the weight diversity. Under this paradigm, the epistemic uncertainty is described by the weight distribution of maximal entropy that produces neural networks "consistent" with the training observations. Considering stochastic neural networks, a practical optimization is derived to build such a distribution, defined as a trade-off between the average empirical risk and the weight distribution entropy. We develop a novel weight parameterization for the stochastic model, based on the singular value decomposition of the neural network's hidden representations, which enables a large increase of the weight entropy for a small empirical risk penalization. We provide both theoretical and numerical results to assess the efficiency of the approach. In particular, the proposed algorithm appears in the top three best methods in all configurations of an extensive out-of-distribution detection benchmark including more than thirty competitors.

Deep Anti-Regularized Ensembles provide reliable out-of-distribution uncertainty quantification

We consider the problem of uncertainty quantification in high dimensional regression and classification for which deep ensemble have proven to be promising methods. Recent observations have shown that deep ensemble often return overconfident estimates outside the training domain, which is a major limitation because shifted distributions are often encountered in real-life scenarios. The principal challenge for this problem is to solve the trade-off between increasing the diversity of the ensemble outputs and making accurate in-distribution predictions. In this work, we show that an ensemble of networks with large weights fitting the training data are likely to meet these two objectives. We derive a simple and practical approach to produce such ensembles, based on an original anti-regularization term penalizing small weights and a control process of the weight increase which maintains the in-distribution loss under an acceptable threshold. The developed approach does not require any out-of-distribution training data neither any trade-off hyper-parameter calibration. We derive a theoretical framework for this approach and show that the proposed optimization can be seen as a "water-filling" problem. Several experiments in both regression and classification settings highlight that Deep Anti-Regularized Ensembles (DARE) significantly improve uncertainty quantification outside the training domain in comparison to recent deep ensembles and out-of-distribution detection methods. All the conducted experiments are reproducible and the source code is available at \url{https://github.com/antoinedemathelin/DARE}.

Online Centralized Non-parametric Change-point Detection via Graph-based Likelihood-ratio Estimation

Consider each node of a graph to be generating a data stream that is synchronized and observed at near real-time. At a change-point $\tau$, a change occurs at a subset of nodes $C$, which affects the probability distribution of their associated node streams. In this paper, we propose a novel kernel-based method to both detect $\tau$ and localize $C$, based on the direct estimation of the likelihood-ratio between the post-change and the pre-change distributions of the node streams. Our main working hypothesis is the smoothness of the likelihood-ratio estimates over the graph, i.e connected nodes are expected to have similar likelihood-ratios. The quality of the proposed method is demonstrated on extensive experiments on synthetic scenarios.

Fast and Accurate Importance Weighting for Correcting Sample Bias

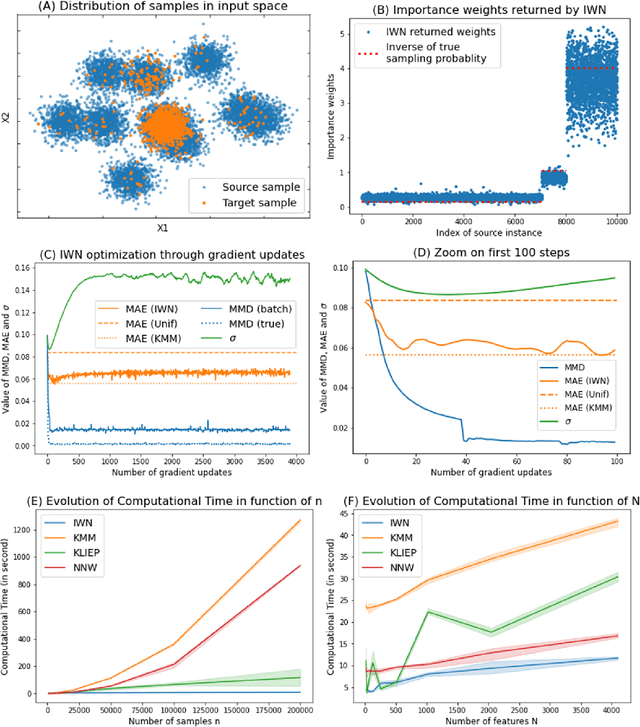
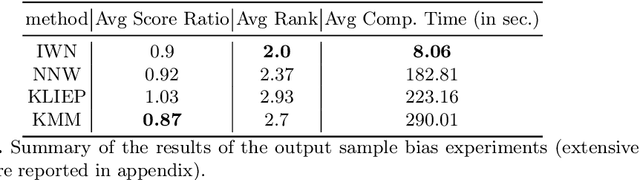
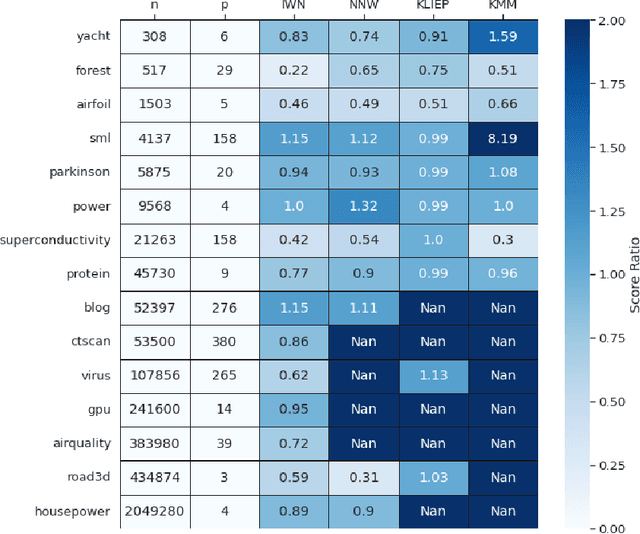
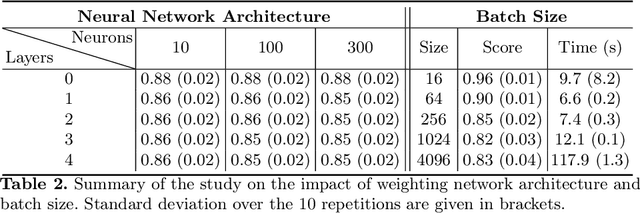
Bias in datasets can be very detrimental for appropriate statistical estimation. In response to this problem, importance weighting methods have been developed to match any biased distribution to its corresponding target unbiased distribution. The seminal Kernel Mean Matching (KMM) method is, nowadays, still considered as state of the art in this research field. However, one of the main drawbacks of this method is the computational burden for large datasets. Building on previous works by Huang et al. (2007) and de Mathelin et al. (2021), we derive a novel importance weighting algorithm which scales to large datasets by using a neural network to predict the instance weights. We show, on multiple public datasets, under various sample biases, that our proposed approach drastically reduces the computational time on large dataset while maintaining similar sample bias correction performance compared to other importance weighting methods. The proposed approach appears to be the only one able to give relevant reweighting in a reasonable time for large dataset with up to two million data.