Leveraging Graph Neural Networks to Forecast Electricity Consumption

Accurate electricity demand forecasting is essential for several reasons, especially as the integration of renewable energy sources and the transition to a decentralized network paradigm introduce greater complexity and uncertainty. The proposed methodology leverages graph-based representations to effectively capture the spatial distribution and relational intricacies inherent in this decentralized network structure. This research work offers a novel approach that extends beyond the conventional Generalized Additive Model framework by considering models like Graph Convolutional Networks or Graph SAGE. These graph-based models enable the incorporation of various levels of interconnectedness and information sharing among nodes, where each node corresponds to the combined load (i.e. consumption) of a subset of consumers (e.g. the regions of a country). More specifically, we introduce a range of methods for inferring graphs tailored to consumption forecasting, along with a framework for evaluating the developed models in terms of both performance and explainability. We conduct experiments on electricity forecasting, in both a synthetic and a real framework considering the French mainland regions, and the performance and merits of our approach are discussed.

Stein Boltzmann Sampling: A Variational Approach for Global Optimization

In this paper, we introduce a new flow-based method for global optimization of Lipschitz functions, called Stein Boltzmann Sampling (SBS). Our method samples from the Boltzmann distribution that becomes asymptotically uniform over the set of the minimizers of the function to be optimized. Candidate solutions are sampled via the \emph{Stein Variational Gradient Descent} algorithm. We prove the asymptotic convergence of our method, introduce two SBS variants, and provide a detailed comparison with several state-of-the-art global optimization algorithms on various benchmark functions. The design of our method, the theoretical results, and our experiments, suggest that SBS is particularly well-suited to be used as a continuation of efficient global optimization methods as it can produce better solutions while making a good use of the budget.

Collaborative non-parametric two-sample testing

This paper addresses the multiple two-sample test problem in a graph-structured setting, which is a common scenario in fields such as Spatial Statistics and Neuroscience. Each node $v$ in fixed graph deals with a two-sample testing problem between two node-specific probability density functions (pdfs), $p_v$ and $q_v$. The goal is to identify nodes where the null hypothesis $p_v = q_v$ should be rejected, under the assumption that connected nodes would yield similar test outcomes. We propose the non-parametric collaborative two-sample testing (CTST) framework that efficiently leverages the graph structure and minimizes the assumptions over $p_v$ and $q_v$. Our methodology integrates elements from f-divergence estimation, Kernel Methods, and Multitask Learning. We use synthetic experiments and a real sensor network detecting seismic activity to demonstrate that CTST outperforms state-of-the-art non-parametric statistical tests that apply at each node independently, hence disregard the geometry of the problem.

UniForCE: The Unimodality Forest Method for Clustering and Estimation of the Number of Clusters

Estimating the number of clusters k while clustering the data is a challenging task. An incorrect cluster assumption indicates that the number of clusters k gets wrongly estimated. Consequently, the model fitting becomes less important. In this work, we focus on the concept of unimodality and propose a flexible cluster definition called locally unimodal cluster. A locally unimodal cluster extends for as long as unimodality is locally preserved across pairs of subclusters of the data. Then, we propose the UniForCE method for locally unimodal clustering. The method starts with an initial overclustering of the data and relies on the unimodality graph that connects subclusters forming unimodal pairs. Such pairs are identified using an appropriate statistical test. UniForCE identifies maximal locally unimodal clusters by computing a spanning forest in the unimodality graph. Experimental results on both real and synthetic datasets illustrate that the proposed methodology is particularly flexible and robust in discovering regular and highly complex cluster shapes. Most importantly, it automatically provides an adequate estimation of the number of clusters.

Online non-parametric likelihood-ratio estimation by Pearson-divergence functional minimization

Quantifying the difference between two probability density functions, $p$ and $q$, using available data, is a fundamental problem in Statistics and Machine Learning. A usual approach for addressing this problem is the likelihood-ratio estimation (LRE) between $p$ and $q$, which -- to our best knowledge -- has been investigated mainly for the offline case. This paper contributes by introducing a new framework for online non-parametric LRE (OLRE) for the setting where pairs of iid observations $(x_t \sim p, x'_t \sim q)$ are observed over time. The non-parametric nature of our approach has the advantage of being agnostic to the forms of $p$ and $q$. Moreover, we capitalize on the recent advances in Kernel Methods and functional minimization to develop an estimator that can be efficiently updated online. We provide theoretical guarantees for the performance of the OLRE method along with empirical validation in synthetic experiments.

A framework for paired-sample hypothesis testing for high-dimensional data

The standard paired-sample testing approach in the multidimensional setting applies multiple univariate tests on the individual features, followed by p-value adjustments. Such an approach suffers when the data carry numerous features. A number of studies have shown that classification accuracy can be seen as a proxy for two-sample testing. However, neither theoretical foundations nor practical recipes have been proposed so far on how this strategy could be extended to multidimensional paired-sample testing. In this work, we put forward the idea that scoring functions can be produced by the decision rules defined by the perpendicular bisecting hyperplanes of the line segments connecting each pair of instances. Then, the optimal scoring function can be obtained by the pseudomedian of those rules, which we estimate by extending naturally the Hodges-Lehmann estimator. We accordingly propose a framework of a two-step testing procedure. First, we estimate the bisecting hyperplanes for each pair of instances and an aggregated rule derived through the Hodges-Lehmann estimator. The paired samples are scored by this aggregated rule to produce a unidimensional representation. Second, we perform a Wilcoxon signed-rank test on the obtained representation. Our experiments indicate that our approach has substantial performance gains in testing accuracy compared to the traditional multivariate and multiple testing, while at the same time estimates each feature's contribution to the final result.

Online Centralized Non-parametric Change-point Detection via Graph-based Likelihood-ratio Estimation

Consider each node of a graph to be generating a data stream that is synchronized and observed at near real-time. At a change-point $\tau$, a change occurs at a subset of nodes $C$, which affects the probability distribution of their associated node streams. In this paper, we propose a novel kernel-based method to both detect $\tau$ and localize $C$, based on the direct estimation of the likelihood-ratio between the post-change and the pre-change distributions of the node streams. Our main working hypothesis is the smoothness of the likelihood-ratio estimates over the graph, i.e connected nodes are expected to have similar likelihood-ratios. The quality of the proposed method is demonstrated on extensive experiments on synthetic scenarios.

To tree or not to tree? Assessing the impact of smoothing the decision boundaries

When analyzing a dataset, it can be useful to assess how smooth the decision boundaries need to be for a model to better fit the data. This paper addresses this question by proposing the quantification of how much should the 'rigid' decision boundaries, produced by an algorithm that naturally finds such solutions, be relaxed to obtain a performance improvement. The approach we propose starts with the rigid decision boundaries of a seed Decision Tree (seed DT), which is used to initialize a Neural DT (NDT). The initial boundaries are challenged by relaxing them progressively through training the NDT. During this process, we measure the NDT's performance and decision agreement to its seed DT. We show how these two measures can help the user in figuring out how expressive his model should be, before exploring it further via model selection. The validity of our approach is demonstrated with experiments on simulated and benchmark datasets.

Clustering for directed graphs using parametrized random walk diffusion kernels

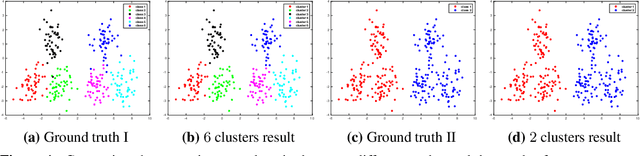
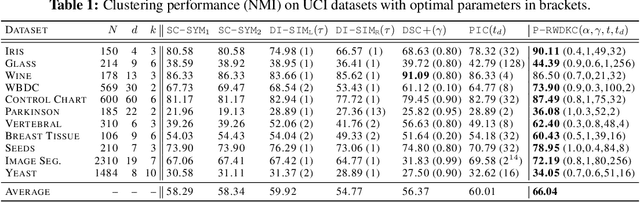
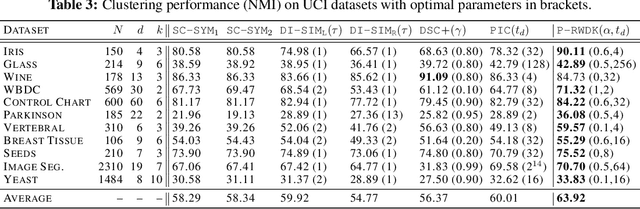
Clustering based on the random walk operator has been proven effective for undirected graphs, but its generalization to directed graphs (digraphs) is much more challenging. Although the random walk operator is well-defined for digraphs, in most cases such graphs are not strongly connected, and hence the associated random walks are not irreducible, which is a crucial property for clustering that exists naturally in the undirected setting. To remedy this, the usual workaround is to either naively symmetrize the adjacency matrix or to replace the natural random walk operator by the teleporting random walk operator, but this can lead to the loss of valuable information carried by edge directionality. In this paper, we introduce a new clustering framework, the Parametrized Random Walk Diffusion Kernel Clustering (P-RWDKC), which is suitable for handling both directed and undirected graphs. Our framework is based on the diffusion geometry and the generalized spectral clustering framework. Accordingly, we propose an algorithm that automatically reveals the cluster structure at a given scale, by considering the random walk dynamics associated with a parametrized kernel operator, and by estimating its critical diffusion time. Experiments on $K$-NN graphs constructed from real-world datasets and real-world graphs show that our clustering approach performs well in all tested cases, and outperforms existing approaches in most of them.

Collaborative likelihood-ratio estimation over graphs

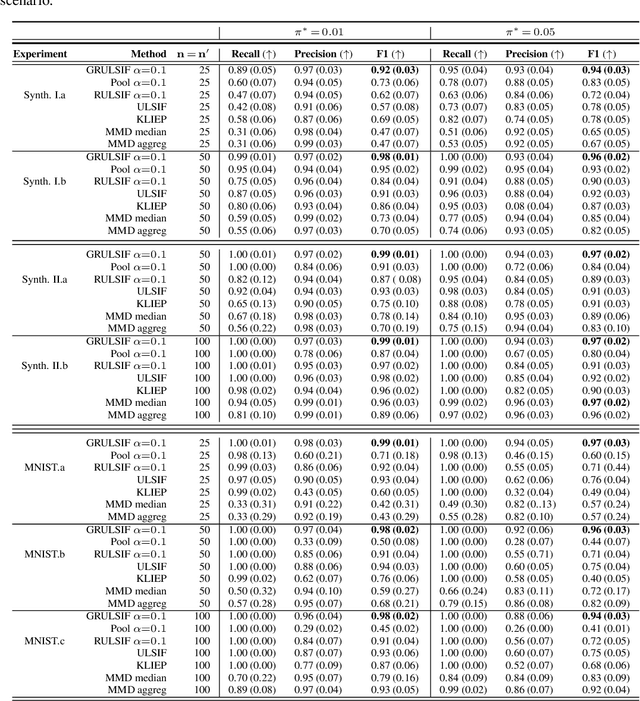
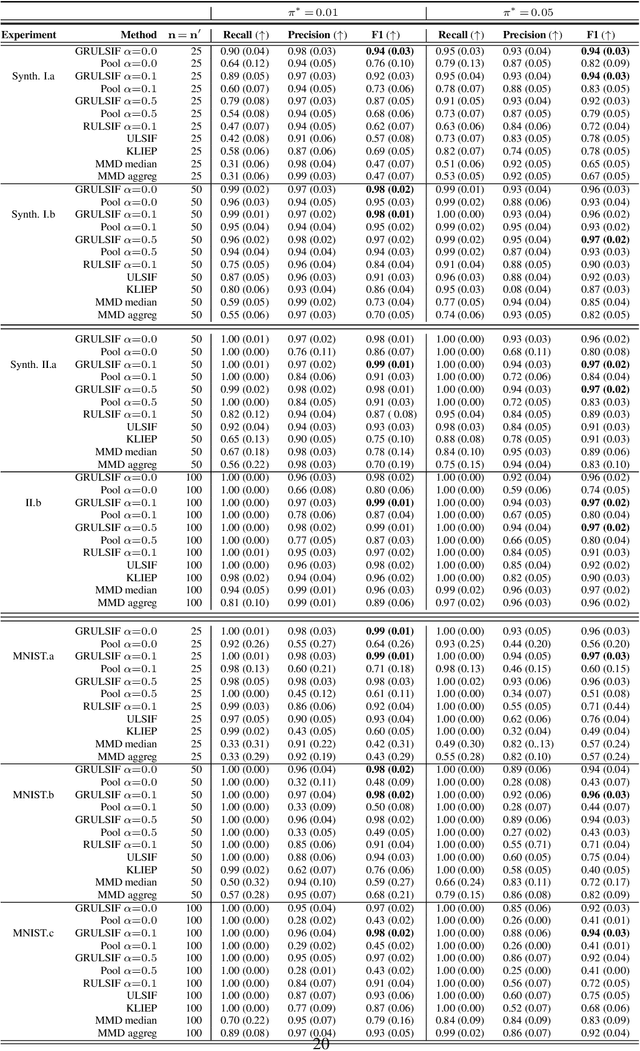
Assuming we have i.i.d observations from two unknown probability density functions (pdfs), $p$ and $p'$, the likelihood-ratio estimation (LRE) is an elegant approach to compare the two pdfs just by relying on the available data, and without knowing the pdfs explicitly. In this paper we introduce a graph-based extension of this problem: Suppose each node $v$ of a fixed graph has access to observations coming from two unknown node-specific pdfs, $p_v$ and $p'_v$; the goal is then to compare the respective $p_v$ and $p'_v$ of each node by also integrating information provided by the graph structure. This setting is interesting when the graph conveys some sort of `similarity' between the node-wise estimation tasks, which suggests that the nodes can collaborate to solve more efficiently their individual tasks, while on the other hand trying to limit the data sharing among them. Our main contribution is a distributed non-parametric framework for graph-based LRE, called GRULSIF, that incorporates in a novel way elements from f-divengence functionals, Kernel methods, and Multitask Learning. Among the several applications of LRE, we choose the two-sample hypothesis testing to develop a proof of concept for our graph-based learning framework. Our experiments compare favorably the performance of our approach against state-of-the-art non-parametric statistical tests that apply at each node independently, and thus disregard the graph structure.