Clustering for directed graphs using parametrized random walk diffusion kernels

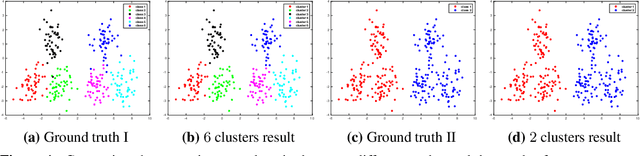
Clustering based on the random walk operator has been proven effective for undirected graphs, but its generalization to directed graphs (digraphs) is much more challenging. Although the random walk operator is well-defined for digraphs, in most cases such graphs are not strongly connected, and hence the associated random walks are not irreducible, which is a crucial property for clustering that exists naturally in the undirected setting. To remedy this, the usual workaround is to either naively symmetrize the adjacency matrix or to replace the natural random walk operator by the teleporting random walk operator, but this can lead to the loss of valuable information carried by edge directionality. In this paper, we introduce a new clustering framework, the Parametrized Random Walk Diffusion Kernel Clustering (P-RWDKC), which is suitable for handling both directed and undirected graphs. Our framework is based on the diffusion geometry and the generalized spectral clustering framework. Accordingly, we propose an algorithm that automatically reveals the cluster structure at a given scale, by considering the random walk dynamics associated with a parametrized kernel operator, and by estimating its critical diffusion time. Experiments on $K$-NN graphs constructed from real-world datasets and real-world graphs show that our clustering approach performs well in all tested cases, and outperforms existing approaches in most of them.

Generalized Spectral Clustering for Directed and Undirected Graphs

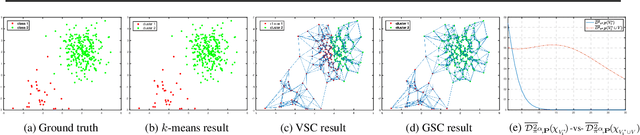
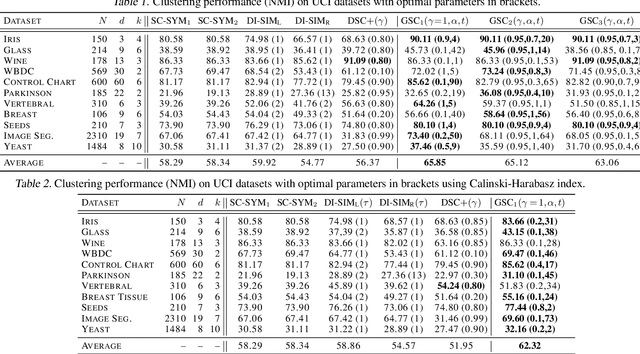
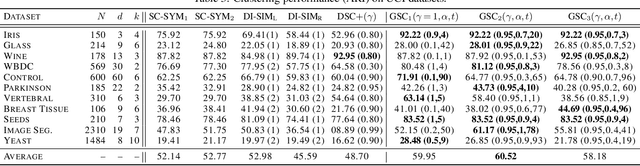
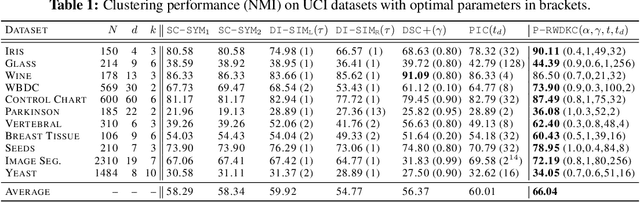
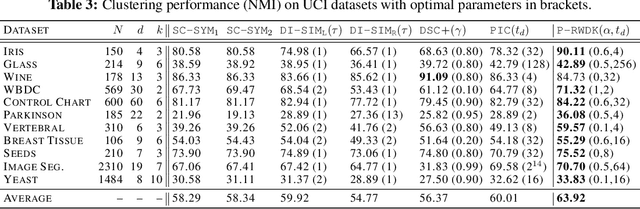
Spectral clustering is a popular approach for clustering undirected graphs, but its extension to directed graphs (digraphs) is much more challenging. A typical workaround is to naively symmetrize the adjacency matrix of the directed graph, which can however lead to discarding valuable information carried by edge directionality. In this paper, we present a generalized spectral clustering framework that can address both directed and undirected graphs. Our approach is based on the spectral relaxation of a new functional that we introduce as the generalized Dirichlet energy of a graph function, with respect to an arbitrary positive regularizing measure on the graph edges. We also propose a practical parametrization of the regularizing measure constructed from the iterated powers of the natural random walk on the graph. We present theoretical arguments to explain the efficiency of our framework in the challenging setting of unbalanced classes. Experiments using directed K-NN graphs constructed from real datasets show that our graph partitioning method performs consistently well in all cases, while outperforming existing approaches in most of them.

Harmonic analysis on directed graphs and applications: from Fourier analysis to wavelets

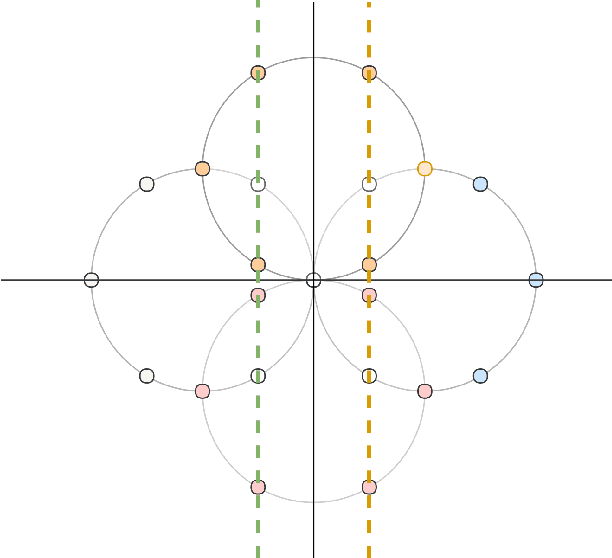
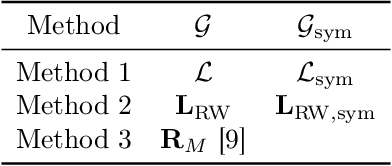
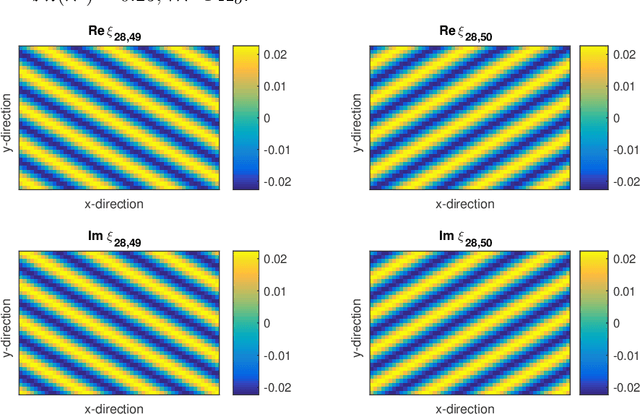
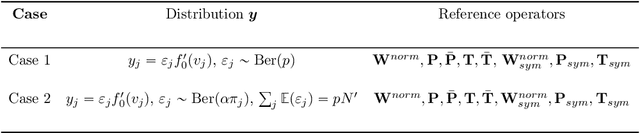
We introduce a novel harmonic analysis for functions defined on the vertices of a strongly connected directed graph of which the random walk operator is the cornerstone. As a first step, we consider the set of eigenvectors of the random walk operator as a non-orthogonal Fourier-type basis for functions over directed graphs. We found a frequency interpretation by linking the variation of the eigenvectors of the random walk operator obtained from their Dirichlet energy to the real part of their associated eigenvalues. From this Fourier basis, we can proceed further and build multi-scale analyses on directed graphs. We propose both a redundant wavelet transform and a decimated wavelet transform by extending the diffusion wavelets framework by Coifman and Maggioni for directed graphs. The development of our harmonic analysis on directed graphs thus leads us to consider both semi-supervised learning problems and signal modeling problems on graphs applied to directed graphs highlighting the efficiency of our framework.

The Asymptotic Performance of Linear Echo State Neural Networks

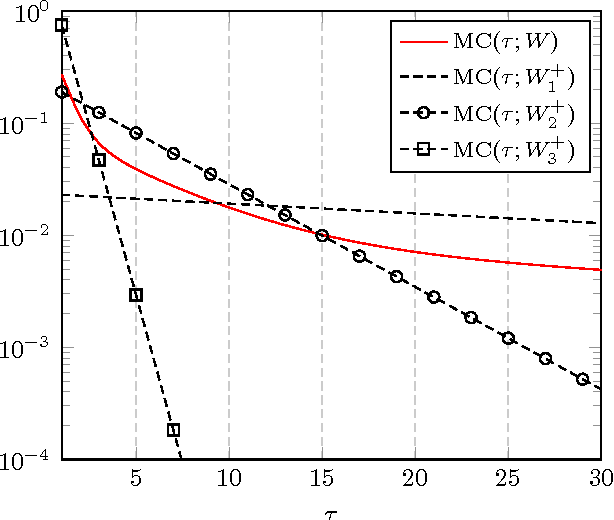
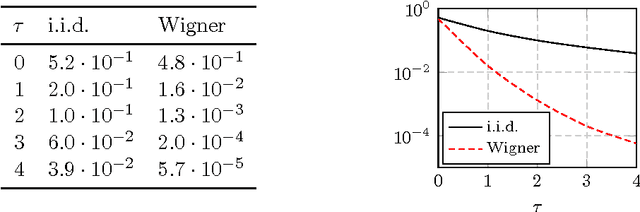
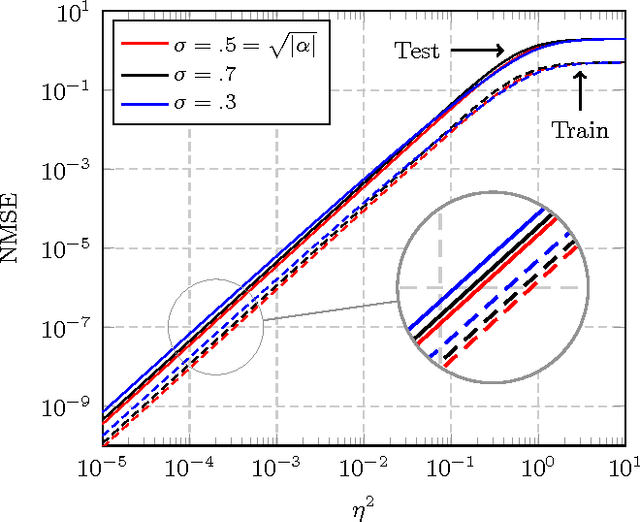
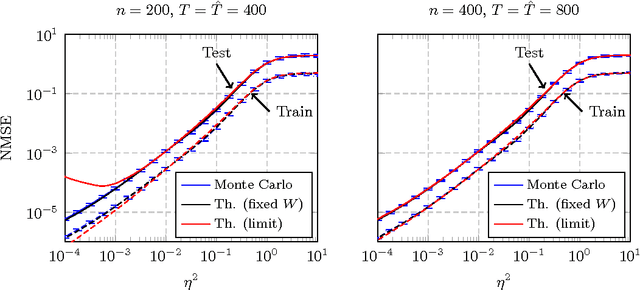
In this article, a study of the mean-square error (MSE) performance of linear echo-state neural networks is performed, both for training and testing tasks. Considering the realistic setting of noise present at the network nodes, we derive deterministic equivalents for the aforementioned MSE in the limit where the number of input data $T$ and network size $n$ both grow large. Specializing then the network connectivity matrix to specific random settings, we further obtain simple formulas that provide new insights on the performance of such networks.