Human in the Loop Adaptive Optimization for Improved Time Series Forecasting

Time series forecasting models often produce systematic, predictable errors even in critical domains such as energy, finance, and healthcare. We introduce a novel post training adaptive optimization framework that improves forecast accuracy without retraining or architectural changes. Our method automatically applies expressive transformations optimized via reinforcement learning, contextual bandits, or genetic algorithms to correct model outputs in a lightweight and model agnostic way. Theoretically, we prove that affine corrections always reduce the mean squared error; practically, we extend this idea with dynamic action based optimization. The framework also supports an optional human in the loop component: domain experts can guide corrections using natural language, which is parsed into actions by a language model. Across multiple benchmarks (e.g., electricity, weather, traffic), we observe consistent accuracy gains with minimal computational overhead. Our interactive demo shows the framework's real time usability. By combining automated post hoc refinement with interpretable and extensible mechanisms, our approach offers a powerful new direction for practical forecasting systems.

Deep Neural Network Models Trained With A Fixed Random Classifier Transfer Better Across Domains

The recently discovered Neural collapse (NC) phenomenon states that the last-layer weights of Deep Neural Networks (DNN), converge to the so-called Equiangular Tight Frame (ETF) simplex, at the terminal phase of their training. This ETF geometry is equivalent to vanishing within-class variability of the last layer activations. Inspired by NC properties, we explore in this paper the transferability of DNN models trained with their last layer weight fixed according to ETF. This enforces class separation by eliminating class covariance information, effectively providing implicit regularization. We show that DNN models trained with such a fixed classifier significantly improve transfer performance, particularly on out-of-domain datasets. On a broad range of fine-grained image classification datasets, our approach outperforms i) baseline methods that do not perform any covariance regularization (up to 22%), as well as ii) methods that explicitly whiten covariance of activations throughout training (up to 19%). Our findings suggest that DNNs trained with fixed ETF classifiers offer a powerful mechanism for improving transfer learning across domains.

Random matrices in service of ML footprint: ternary random features with no performance loss

In this article, we investigate the spectral behavior of random features kernel matrices of the type ${\bf K} = \mathbb{E}_{{\bf w}} \left[\sigma\left({\bf w}^{\sf T}{\bf x}_i\right)\sigma\left({\bf w}^{\sf T}{\bf x}_j\right)\right]_{i,j=1}^n$, with nonlinear function $\sigma(\cdot)$, data ${\bf x}_1, \ldots, {\bf x}_n \in \mathbb{R}^p$, and random projection vector ${\bf w} \in \mathbb{R}^p$ having i.i.d. entries. In a high-dimensional setting where the number of data $n$ and their dimension $p$ are both large and comparable, we show, under a Gaussian mixture model for the data, that the eigenspectrum of ${\bf K}$ is independent of the distribution of the i.i.d.(zero-mean and unit-variance) entries of ${\bf w}$, and only depends on $\sigma(\cdot)$ via its (generalized) Gaussian moments $\mathbb{E}_{z\sim \mathcal N(0,1)}[\sigma'(z)]$ and $\mathbb{E}_{z\sim \mathcal N(0,1)}[\sigma''(z)]$. As a result, for any kernel matrix ${\bf K}$ of the form above, we propose a novel random features technique, called Ternary Random Feature (TRF), that (i) asymptotically yields the same limiting kernel as the original ${\bf K}$ in a spectral sense and (ii) can be computed and stored much more efficiently, by wisely tuning (in a data-dependent manner) the function $\sigma$ and the random vector ${\bf w}$, both taking values in $\{-1,0,1\}$. The computation of the proposed random features requires no multiplication, and a factor of $b$ times less bits for storage compared to classical random features such as random Fourier features, with $b$ the number of bits to store full precision values. Besides, it appears in our experiments on real data that the substantial gains in computation and storage are accompanied with somewhat improved performances compared to state-of-the-art random features compression/quantization methods.

Latent heterogeneous multilayer community detection

We propose a method for simultaneously detecting shared and unshared communities in heterogeneous multilayer weighted and undirected networks. The multilayer network is assumed to follow a generative probabilistic model that takes into account the similarities and dissimilarities between the communities. We make use of a variational Bayes approach for jointly inferring the shared and unshared hidden communities from multilayer network observations. We show the robustness of our approach compared to state-of-the art algorithms in detecting disparate (shared and private) communities on synthetic data as well as on real genome-wide fibroblast proliferation dataset.

Spectral community detection in heterogeneous large networks

In this article, we study spectral methods for community detection based on $ \alpha$-parametrized normalized modularity matrix hereafter called $ {\bf L}_\alpha $ in heterogeneous graph models. We show, in a regime where community detection is not asymptotically trivial, that $ {\bf L}_\alpha $ can be well approximated by a more tractable random matrix which falls in the family of spiked random matrices. The analysis of this equivalent spiked random matrix allows us to improve spectral methods for community detection and assess their performances in the regime under study. In particular, we prove the existence of an optimal value $ \alpha_{\rm opt} $ of the parameter $ \alpha $ for which the detection of communities is best ensured and we provide an on-line estimation of $ \alpha_{\rm opt} $ only based on the knowledge of the graph adjacency matrix. Unlike classical spectral methods for community detection where clustering is performed on the eigenvectors associated with extreme eigenvalues, we show through our theoretical analysis that a regularization should instead be performed on those eigenvectors prior to clustering in heterogeneous graphs. Finally, through a deeper study of the regularized eigenvectors used for clustering, we assess the performances of our new algorithm for community detection. Numerical simulations in the course of the article show that our methods outperform state-of-the-art spectral methods on dense heterogeneous graphs.

The Asymptotic Performance of Linear Echo State Neural Networks

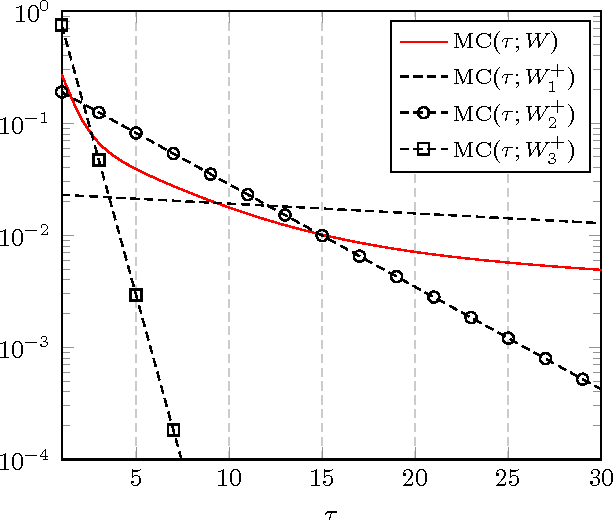
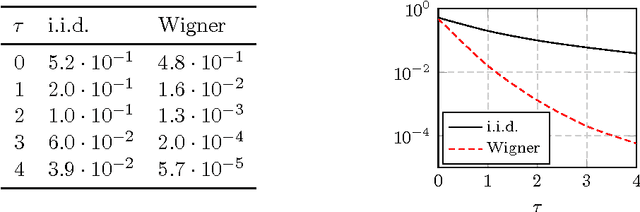
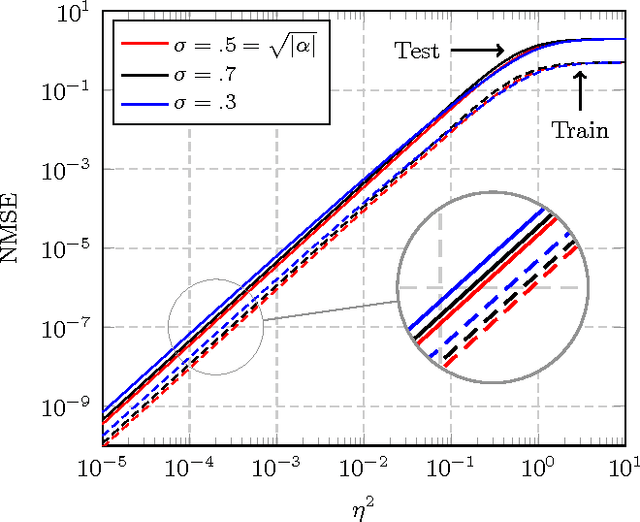
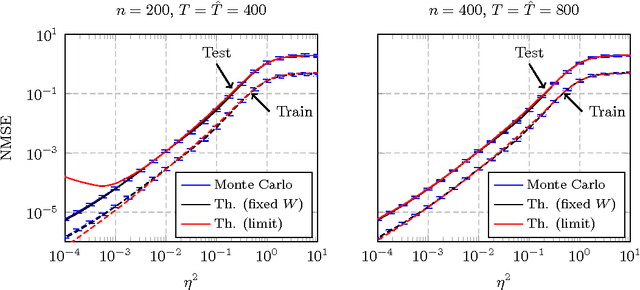
In this article, a study of the mean-square error (MSE) performance of linear echo-state neural networks is performed, both for training and testing tasks. Considering the realistic setting of noise present at the network nodes, we derive deterministic equivalents for the aforementioned MSE in the limit where the number of input data $T$ and network size $n$ both grow large. Specializing then the network connectivity matrix to specific random settings, we further obtain simple formulas that provide new insights on the performance of such networks.