Do Heavy Tails Help Diffusion? On the Subtle Trade-off Between Initialization and Training

Recent works have proposed incorporating heavy-tailed (HT) noise into diffusion- and flow-based generative models, with the goals of better recovering the tails of target distributions and improving generative diversity. This motivation is intuitive: if the data are heavy-tailed, HT noise may appear better matched than light-tailed (LT) Gaussian noise. However, replacing Gaussian noise by HT noise also changes the underlying estimation problem. In this paper, we revisit this paradigm through a combined theoretical and empirical study, establishing sampling-error bounds for two representative diffusion models driven by HT and LT noise. We show that HT noise makes the statistical estimation problem harder, leading to less favorable sampling-error bounds. We support these findings with experiments on synthetic and real-world datasets, empirically recovering the predicted error trade-off. Our results call into question a growing design trend in generative modeling and challenge the use of HT noise to improve rare-region exploration.

Human in the Loop Adaptive Optimization for Improved Time Series Forecasting

Time series forecasting models often produce systematic, predictable errors even in critical domains such as energy, finance, and healthcare. We introduce a novel post training adaptive optimization framework that improves forecast accuracy without retraining or architectural changes. Our method automatically applies expressive transformations optimized via reinforcement learning, contextual bandits, or genetic algorithms to correct model outputs in a lightweight and model agnostic way. Theoretically, we prove that affine corrections always reduce the mean squared error; practically, we extend this idea with dynamic action based optimization. The framework also supports an optional human in the loop component: domain experts can guide corrections using natural language, which is parsed into actions by a language model. Across multiple benchmarks (e.g., electricity, weather, traffic), we observe consistent accuracy gains with minimal computational overhead. Our interactive demo shows the framework's real time usability. By combining automated post hoc refinement with interpretable and extensible mechanisms, our approach offers a powerful new direction for practical forecasting systems.

High-Dimensional Analysis of Bootstrap Ensemble Classifiers

Bootstrap methods have long been a cornerstone of ensemble learning in machine learning. This paper presents a theoretical analysis of bootstrap techniques applied to the Least Square Support Vector Machine (LSSVM) ensemble in the context of large and growing sample sizes and feature dimensionalities. Leveraging tools from Random Matrix Theory, we investigate the performance of this classifier that aggregates decision functions from multiple weak classifiers, each trained on different subsets of the data. We provide insights into the use of bootstrap methods in high-dimensional settings, enhancing our understanding of their impact. Based on these findings, we propose strategies to select the number of subsets and the regularization parameter that maximize the performance of the LSSVM. Empirical experiments on synthetic and real-world datasets validate our theoretical results.

TAG: A Decentralized Framework for Multi-Agent Hierarchical Reinforcement Learning

Hierarchical organization is fundamental to biological systems and human societies, yet artificial intelligence systems often rely on monolithic architectures that limit adaptability and scalability. Current hierarchical reinforcement learning (HRL) approaches typically restrict hierarchies to two levels or require centralized training, which limits their practical applicability. We introduce TAME Agent Framework (TAG), a framework for constructing fully decentralized hierarchical multi-agent systems.TAG enables hierarchies of arbitrary depth through a novel LevelEnv concept, which abstracts each hierarchy level as the environment for the agents above it. This approach standardizes information flow between levels while preserving loose coupling, allowing for seamless integration of diverse agent types. We demonstrate the effectiveness of TAG by implementing hierarchical architectures that combine different RL agents across multiple levels, achieving improved performance over classical multi-agent RL baselines on standard benchmarks. Our results show that decentralized hierarchical organization enhances both learning speed and final performance, positioning TAG as a promising direction for scalable multi-agent systems.

Large Language Models Orchestrating Structured Reasoning Achieve Kaggle Grandmaster Level

We introduce Agent K v1.0, an end-to-end autonomous data science agent designed to automate, optimise, and generalise across diverse data science tasks. Fully automated, Agent K v1.0 manages the entire data science life cycle by learning from experience. It leverages a highly flexible structured reasoning framework to enable it to dynamically process memory in a nested structure, effectively learning from accumulated experience stored to handle complex reasoning tasks. It optimises long- and short-term memory by selectively storing and retrieving key information, guiding future decisions based on environmental rewards. This iterative approach allows it to refine decisions without fine-tuning or backpropagation, achieving continuous improvement through experiential learning. We evaluate our agent's apabilities using Kaggle competitions as a case study. Following a fully automated protocol, Agent K v1.0 systematically addresses complex and multimodal data science tasks, employing Bayesian optimisation for hyperparameter tuning and feature engineering. Our new evaluation framework rigorously assesses Agent K v1.0's end-to-end capabilities to generate and send submissions starting from a Kaggle competition URL. Results demonstrate that Agent K v1.0 achieves a 92.5\% success rate across tasks, spanning tabular, computer vision, NLP, and multimodal domains. When benchmarking against 5,856 human Kaggle competitors by calculating Elo-MMR scores for each, Agent K v1.0 ranks in the top 38\%, demonstrating an overall skill level comparable to Expert-level users. Notably, its Elo-MMR score falls between the first and third quartiles of scores achieved by human Grandmasters. Furthermore, our results indicate that Agent K v1.0 has reached a performance level equivalent to Kaggle Grandmaster, with a record of 6 gold, 3 silver, and 7 bronze medals, as defined by Kaggle's progression system.

Price of Safety in Linear Best Arm Identification

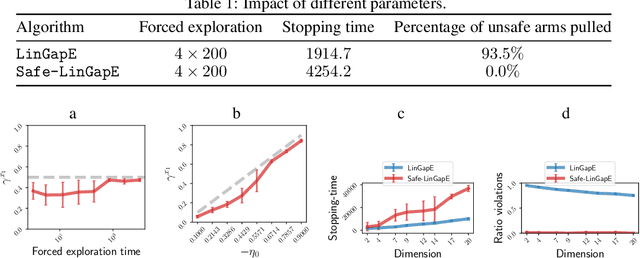
We introduce the safe best-arm identification framework with linear feedback, where the agent is subject to some stage-wise safety constraint that linearly depends on an unknown parameter vector. The agent must take actions in a conservative way so as to ensure that the safety constraint is not violated with high probability at each round. Ways of leveraging the linear structure for ensuring safety has been studied for regret minimization, but not for best-arm identification to the best our knowledge. We propose a gap-based algorithm that achieves meaningful sample complexity while ensuring the stage-wise safety. We show that we pay an extra term in the sample complexity due to the forced exploration phase incurred by the additional safety constraint. Experimental illustrations are provided to justify the design of our algorithm.

Clustered Multi-Agent Linear Bandits

We address in this paper a particular instance of the multi-agent linear stochastic bandit problem, called clustered multi-agent linear bandits. In this setting, we propose a novel algorithm leveraging an efficient collaboration between the agents in order to accelerate the overall optimization problem. In this contribution, a network controller is responsible for estimating the underlying cluster structure of the network and optimizing the experiences sharing among agents within the same groups. We provide a theoretical analysis for both the regret minimization problem and the clustering quality. Through empirical evaluation against state-of-the-art algorithms on both synthetic and real data, we demonstrate the effectiveness of our approach: our algorithm significantly improves regret minimization while managing to recover the true underlying cluster partitioning.

Learning to solve TV regularized problems with unrolled algorithms

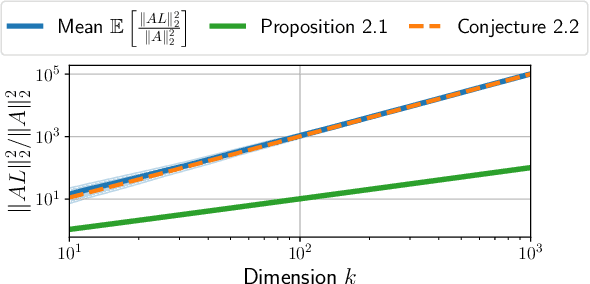
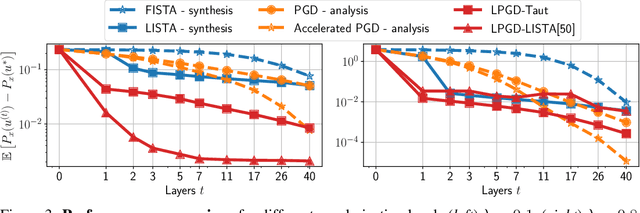
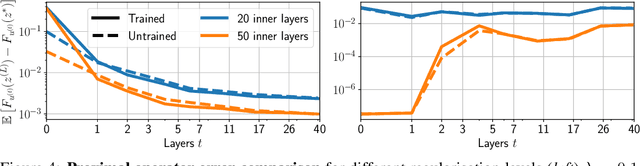
Total Variation (TV) is a popular regularization strategy that promotes piece-wise constant signals by constraining the $\ell_1$-norm of the first order derivative of the estimated signal. The resulting optimization problem is usually solved using iterative algorithms such as proximal gradient descent, primal-dual algorithms or ADMM. However, such methods can require a very large number of iterations to converge to a suitable solution. In this paper, we accelerate such iterative algorithms by unfolding proximal gradient descent solvers in order to learn their parameters for 1D TV regularized problems. While this could be done using the synthesis formulation, we demonstrate that this leads to slower performances. The main difficulty in applying such methods in the analysis formulation lies in proposing a way to compute the derivatives through the proximal operator. As our main contribution, we develop and characterize two approaches to do so, describe their benefits and limitations, and discuss the regime where they can actually improve over iterative procedures. We validate those findings with experiments on synthetic and real data.