Analysing Multi-Task Regression via Random Matrix Theory with Application to Time Series Forecasting

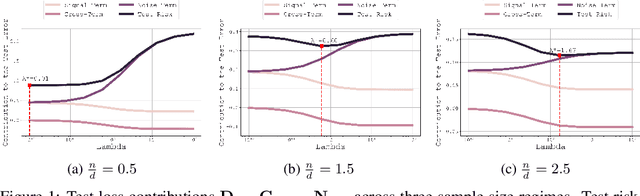
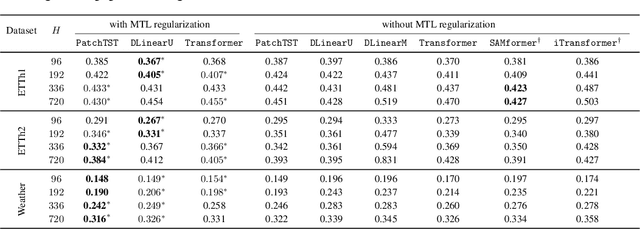
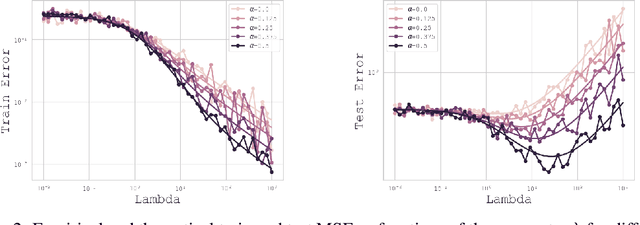
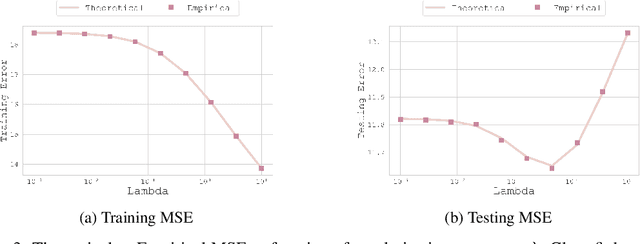
In this paper, we introduce a novel theoretical framework for multi-task regression, applying random matrix theory to provide precise performance estimations, under high-dimensional, non-Gaussian data distributions. We formulate a multi-task optimization problem as a regularization technique to enable single-task models to leverage multi-task learning information. We derive a closed-form solution for multi-task optimization in the context of linear models. Our analysis provides valuable insights by linking the multi-task learning performance to various model statistics such as raw data covariances, signal-generating hyperplanes, noise levels, as well as the size and number of datasets. We finally propose a consistent estimation of training and testing errors, thereby offering a robust foundation for hyperparameter optimization in multi-task regression scenarios. Experimental validations on both synthetic and real-world datasets in regression and multivariate time series forecasting demonstrate improvements on univariate models, incorporating our method into the training loss and thus leveraging multivariate information.

Spectral properties of sample covariance matrices arising from random matrices with independent non identically distributed columns

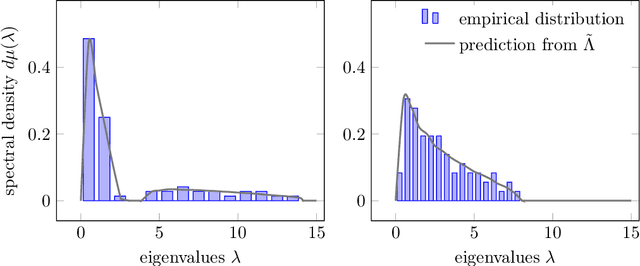
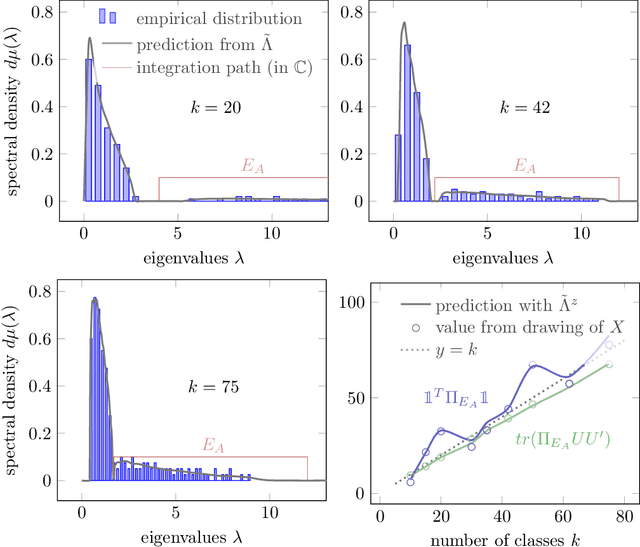
Given a random matrix $X= (x_1,\ldots, x_n)\in \mathcal M_{p,n}$ with independent columns and satisfying concentration of measure hypotheses and a parameter $z$ whose distance to the spectrum of $\frac{1}{n} XX^T$ should not depend on $p,n$, it was previously shown that the functionals $\text{tr}(AR(z))$, for $R(z) = (\frac{1}{n}XX^T- zI_p)^{-1}$ and $A\in \mathcal M_{p}$ deterministic, have a standard deviation of order $O(\|A\|_* / \sqrt n)$. Here, we show that $\|\mathbb E[R(z)] - \tilde R(z)\|_F \leq O(1/\sqrt n)$, where $\tilde R(z)$ is a deterministic matrix depending only on $z$ and on the means and covariances of the column vectors $x_1,\ldots, x_n$ (that do not have to be identically distributed). This estimation is key to providing accurate fluctuation rates of functionals of $X$ of interest (mostly related to its spectral properties) and is proved thanks to the introduction of a semi-metric $d_s$ defined on the set $\mathcal D_n(\mathbb H)$ of diagonal matrices with complex entries and positive imaginary part and satisfying, for all $D,D' \in \mathcal D_n(\mathbb H)$: $d_s(D,D') = \max_{i\in[n]} |D_i - D_i'|/ (\Im(D_i) \Im(D_i'))^{1/2}$. Possibly most importantly, the underlying concentration of measure assumption on the columns of $X$ finds an extremely natural ground for application in modern statistical machine learning algorithms where non-linear Lipschitz mappings and high number of classes form the base ingredients.

Concentration of measure and generalized product of random vectors with an application to Hanson-Wright-like inequalities

Starting from concentration of measure hypotheses on $m$ random vectors $Z_1,\ldots, Z_m$, this article provides an expression of the concentration of functionals $\phi(Z_1,\ldots, Z_m)$ where the variations of $\phi$ on each variable depend on the product of the norms (or semi-norms) of the other variables (as if $\phi$ were a product). We illustrate the importance of this result through various generalizations of the Hanson-Wright concentration inequality as well as through a study of the random matrix $XDX^T$ and its resolvent $Q = (I_p - \frac{1}{n}XDX^T)^{-1}$, where $X$ and $D$ are random, which have fundamental interest in statistical machine learning applications.

Concentration of solutions to random equations with concentration of measure hypotheses

We propose here to study the concentration of random objects that are implicitly formulated as fixed points to equations $Y = f(X)$ where $f$ is a random mapping. Starting from an hypothesis taken from the concentration of the measure theory, we are able to express precisely the concentration of such solutions, under some contractivity hypothesis on $f$. This statement has important implication to random matrix theory, and is at the basis of the study of some optimization procedures like the logistic regression for instance. In those last cases, we give precise estimations to the first statistics of the solution $Y$ which allows us predict the performances of the algorithm.

A Concentration of Measure and Random Matrix Approach to Large Dimensional Robust Statistics

This article studies the \emph{robust covariance matrix estimation} of a data collection $X = (x_1,\ldots,x_n)$ with $x_i = \sqrt \tau_i z_i + m$, where $z_i \in \mathbb R^p$ is a \textit{concentrated vector} (e.g., an elliptical random vector), $m\in \mathbb R^p$ a deterministic signal and $\tau_i\in \mathbb R$ a scalar perturbation of possibly large amplitude, under the assumption where both $n$ and $p$ are large. This estimator is defined as the fixed point of a function which we show is contracting for a so-called \textit{stable semi-metric}. We exploit this semi-metric along with concentration of measure arguments to prove the existence and uniqueness of the robust estimator as well as evaluate its limiting spectral distribution.

Random Matrix Theory Proves that Deep Learning Representations of GAN-data Behave as Gaussian Mixtures

This paper shows that deep learning (DL) representations of data produced by generative adversarial nets (GANs) are random vectors which fall within the class of so-called \textit{concentrated} random vectors. Further exploiting the fact that Gram matrices, of the type $G = X^T X$ with $X=[x_1,\ldots,x_n]\in \mathbb{R}^{p\times n}$ and $x_i$ independent concentrated random vectors from a mixture model, behave asymptotically (as $n,p\to \infty$) as if the $x_i$ were drawn from a Gaussian mixture, suggests that DL representations of GAN-data can be fully described by their first two statistical moments for a wide range of standard classifiers. Our theoretical findings are validated by generating images with the BigGAN model and across different popular deep representation networks.

A Random Matrix Approach to Neural Networks

This article studies the Gram random matrix model $G=\frac1T\Sigma^{\rm T}\Sigma$, $\Sigma=\sigma(WX)$, classically found in the analysis of random feature maps and random neural networks, where $X=[x_1,\ldots,x_T]\in{\mathbb R}^{p\times T}$ is a (data) matrix of bounded norm, $W\in{\mathbb R}^{n\times p}$ is a matrix of independent zero-mean unit variance entries, and $\sigma:{\mathbb R}\to{\mathbb R}$ is a Lipschitz continuous (activation) function --- $\sigma(WX)$ being understood entry-wise. By means of a key concentration of measure lemma arising from non-asymptotic random matrix arguments, we prove that, as $n,p,T$ grow large at the same rate, the resolvent $Q=(G+\gamma I_T)^{-1}$, for $\gamma>0$, has a similar behavior as that met in sample covariance matrix models, involving notably the moment $\Phi=\frac{T}n{\mathbb E}[G]$, which provides in passing a deterministic equivalent for the empirical spectral measure of $G$. Application-wise, this result enables the estimation of the asymptotic performance of single-layer random neural networks. This in turn provides practical insights into the underlying mechanisms into play in random neural networks, entailing several unexpected consequences, as well as a fast practical means to tune the network hyperparameters.