Spectral properties of sample covariance matrices arising from random matrices with independent non identically distributed columns
Paper and Code
Sep 06, 2021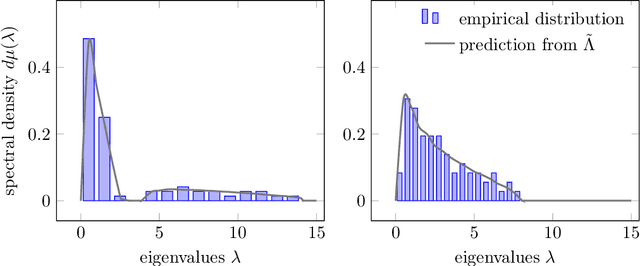
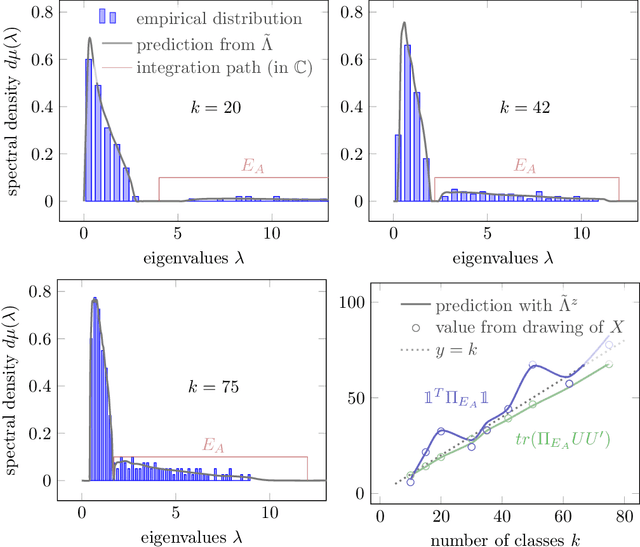
Given a random matrix $X= (x_1,\ldots, x_n)\in \mathcal M_{p,n}$ with independent columns and satisfying concentration of measure hypotheses and a parameter $z$ whose distance to the spectrum of $\frac{1}{n} XX^T$ should not depend on $p,n$, it was previously shown that the functionals $\text{tr}(AR(z))$, for $R(z) = (\frac{1}{n}XX^T- zI_p)^{-1}$ and $A\in \mathcal M_{p}$ deterministic, have a standard deviation of order $O(\|A\|_* / \sqrt n)$. Here, we show that $\|\mathbb E[R(z)] - \tilde R(z)\|_F \leq O(1/\sqrt n)$, where $\tilde R(z)$ is a deterministic matrix depending only on $z$ and on the means and covariances of the column vectors $x_1,\ldots, x_n$ (that do not have to be identically distributed). This estimation is key to providing accurate fluctuation rates of functionals of $X$ of interest (mostly related to its spectral properties) and is proved thanks to the introduction of a semi-metric $d_s$ defined on the set $\mathcal D_n(\mathbb H)$ of diagonal matrices with complex entries and positive imaginary part and satisfying, for all $D,D' \in \mathcal D_n(\mathbb H)$: $d_s(D,D') = \max_{i\in[n]} |D_i - D_i'|/ (\Im(D_i) \Im(D_i'))^{1/2}$. Possibly most importantly, the underlying concentration of measure assumption on the columns of $X$ finds an extremely natural ground for application in modern statistical machine learning algorithms where non-linear Lipschitz mappings and high number of classes form the base ingredients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge