Measuring Pre-training Data Quality without Labels for Time Series Foundation Models

Recently, there has been a growing interest in time series foundation models that generalize across different downstream tasks. A key to strong foundation models is a diverse pre-training dataset, which is particularly challenging to collect for time series classification. In this work, we explore the performance of a contrastive-learning-based foundation model as a function of the data used for pre-training. We introduce contrastive accuracy, a new measure to evaluate the quality of the representation space learned by the foundation model. Our experiments reveal the positive correlation between the proposed measure and the accuracy of the model on a collection of downstream tasks. This suggests that the contrastive accuracy can serve as a criterion to search for time series datasets that can enhance the pre-training and improve thereby the foundation model's generalization.

Analysing Multi-Task Regression via Random Matrix Theory with Application to Time Series Forecasting

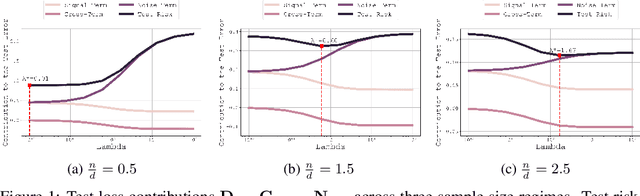
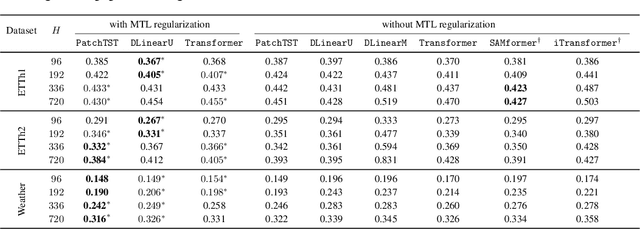
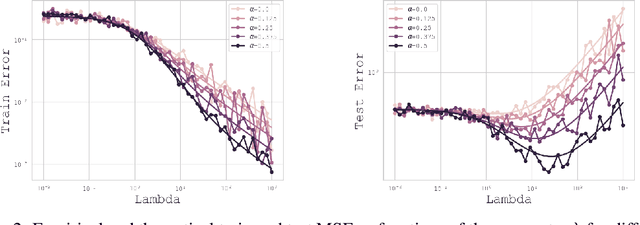
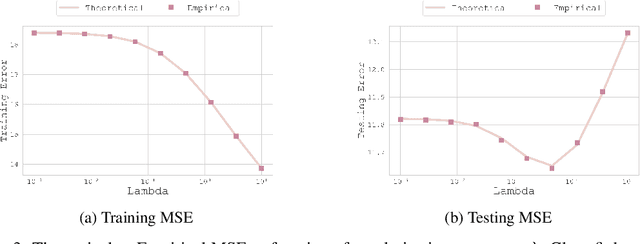
In this paper, we introduce a novel theoretical framework for multi-task regression, applying random matrix theory to provide precise performance estimations, under high-dimensional, non-Gaussian data distributions. We formulate a multi-task optimization problem as a regularization technique to enable single-task models to leverage multi-task learning information. We derive a closed-form solution for multi-task optimization in the context of linear models. Our analysis provides valuable insights by linking the multi-task learning performance to various model statistics such as raw data covariances, signal-generating hyperplanes, noise levels, as well as the size and number of datasets. We finally propose a consistent estimation of training and testing errors, thereby offering a robust foundation for hyperparameter optimization in multi-task regression scenarios. Experimental validations on both synthetic and real-world datasets in regression and multivariate time series forecasting demonstrate improvements on univariate models, incorporating our method into the training loss and thus leveraging multivariate information.

MANO: Exploiting Matrix Norm for Unsupervised Accuracy Estimation Under Distribution Shifts

Leveraging the models' outputs, specifically the logits, is a common approach to estimating the test accuracy of a pre-trained neural network on out-of-distribution (OOD) samples without requiring access to the corresponding ground truth labels. Despite their ease of implementation and computational efficiency, current logit-based methods are vulnerable to overconfidence issues, leading to prediction bias, especially under the natural shift. In this work, we first study the relationship between logits and generalization performance from the view of low-density separation assumption. Our findings motivate our proposed method MaNo which (1) applies a data-dependent normalization on the logits to reduce prediction bias, and (2) takes the $L_p$ norm of the matrix of normalized logits as the estimation score. Our theoretical analysis highlights the connection between the provided score and the model's uncertainty. We conduct an extensive empirical study on common unsupervised accuracy estimation benchmarks and demonstrate that MaNo achieves state-of-the-art performance across various architectures in the presence of synthetic, natural, or subpopulation shifts.

Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention

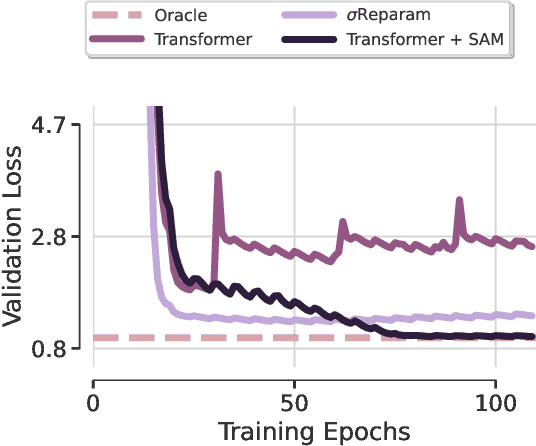
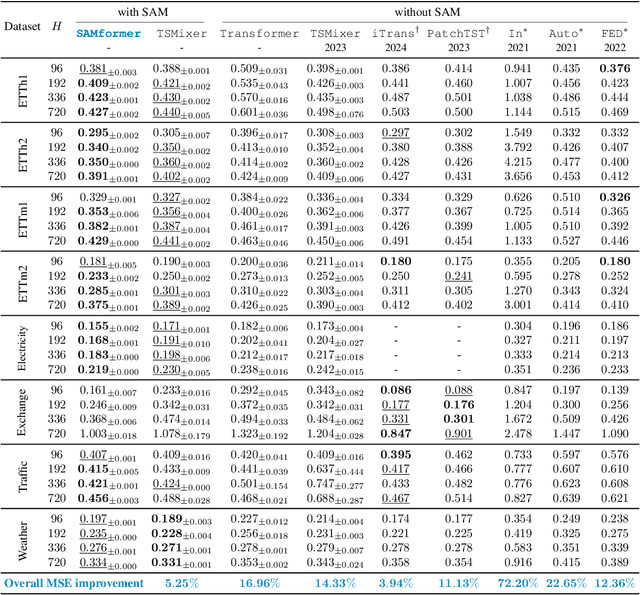
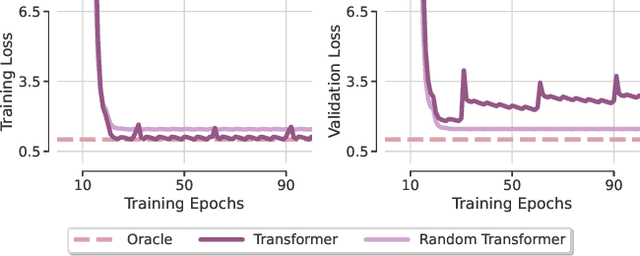
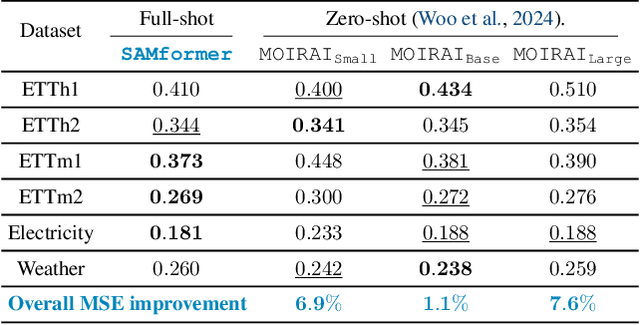
Transformer-based architectures achieved breakthrough performance in natural language processing and computer vision, yet they remain inferior to simpler linear baselines in multivariate long-term forecasting. To better understand this phenomenon, we start by studying a toy linear forecasting problem for which we show that transformers are incapable of converging to their true solution despite their high expressive power. We further identify the attention of transformers as being responsible for this low generalization capacity. Building upon this insight, we propose a shallow lightweight transformer model that successfully escapes bad local minima when optimized with sharpness-aware optimization. We empirically demonstrate that this result extends to all commonly used real-world multivariate time series datasets. In particular, SAMformer surpasses the current state-of-the-art model TSMixer by 14.33% on average, while having ~4 times fewer parameters. The code is available at https://github.com/romilbert/samformer.

Characterising Gradients for Unsupervised Accuracy Estimation under Distribution Shift

Estimating test accuracy without access to the ground-truth test labels under varying test environments is a challenging, yet extremely important problem in the safe deployment of machine learning algorithms. Existing works rely on the information from either the outputs or the extracted features of neural networks to formulate an estimation score correlating with the ground-truth test accuracy. In this paper, we investigate--both empirically and theoretically--how the information provided by the gradients can be predictive of the ground-truth test accuracy even under a distribution shift. Specifically, we use the norm of classification-layer gradients, backpropagated from the cross-entropy loss after only one gradient step over test data. Our key idea is that the model should be adjusted with a higher magnitude of gradients when it does not generalize to the test dataset with a distribution shift. We provide theoretical insights highlighting the main ingredients of such an approach ensuring its empirical success. Extensive experiments conducted on diverse distribution shifts and model structures demonstrate that our method significantly outperforms state-of-the-art algorithms.

Leveraging Ensemble Diversity for Robust Self-Training in the Presence of Sample Selection Bias

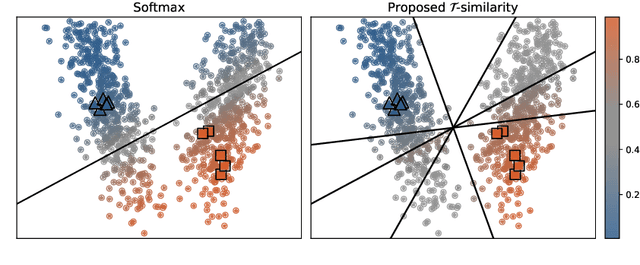
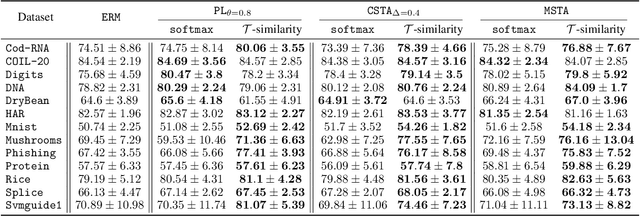
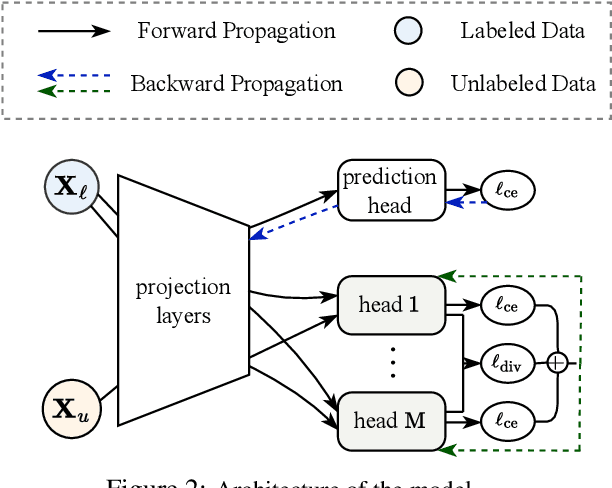
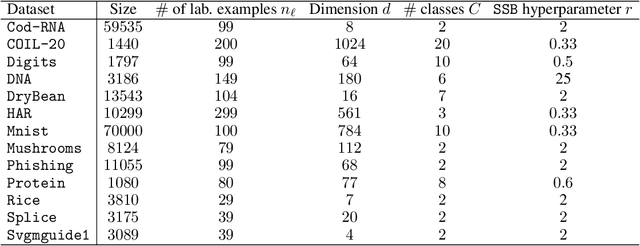
Self-training is a well-known approach for semi-supervised learning. It consists of iteratively assigning pseudo-labels to unlabeled data for which the model is confident and treating them as labeled examples. For neural networks, softmax prediction probabilities are often used as a confidence measure, despite the fact that they are known to be overconfident, even for wrong predictions. This phenomenon is particularly intensified in the presence of sample selection bias, i.e., when data labeling is subject to some constraint. To address this issue, we propose a novel confidence measure, called $\mathcal{T}$-similarity, built upon the prediction diversity of an ensemble of linear classifiers. We provide the theoretical analysis of our approach by studying stationary points and describing the relationship between the diversity of the individual members and their performance. We empirically demonstrate the benefit of our confidence measure for three different pseudo-labeling policies on classification datasets of various data modalities.

Random Matrix Analysis to Balance between Supervised and Unsupervised Learning under the Low Density Separation Assumption

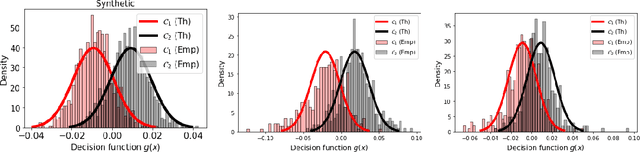
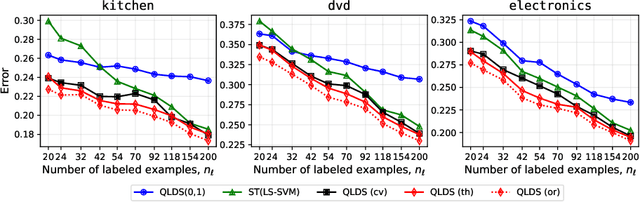
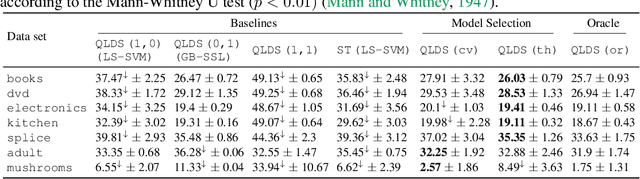
We propose a theoretical framework to analyze semi-supervised classification under the low density separation assumption in a high-dimensional regime. In particular, we introduce QLDS, a linear classification model, where the low density separation assumption is implemented via quadratic margin maximization. The algorithm has an explicit solution with rich theoretical properties, and we show that particular cases of our algorithm are the least-square support vector machine in the supervised case, the spectral clustering in the fully unsupervised regime, and a class of semi-supervised graph-based approaches. As such, QLDS establishes a smooth bridge between these supervised and unsupervised learning methods. Using recent advances in the random matrix theory, we formally derive a theoretical evaluation of the classification error in the asymptotic regime. As an application, we derive a hyperparameter selection policy that finds the best balance between the supervised and the unsupervised terms of our learning criterion. Finally, we provide extensive illustrations of our framework, as well as an experimental study on several benchmarks to demonstrate that QLDS, while being computationally more efficient, improves over cross-validation for hyperparameter selection, indicating a high promise of the usage of random matrix theory for semi-supervised model selection.

Self-Training: A Survey

In recent years, semi-supervised algorithms have received a lot of interest in both academia and industry. Among the existing techniques, self-training methods have arguably received more attention in the last few years. These models are designed to search the decision boundary on low density regions without making extra assumptions on the data distribution, and use the unsigned output score of a learned classifier, or its margin, as an indicator of confidence. The working principle of self-training algorithms is to learn a classifier iteratively by assigning pseudo-labels to the set of unlabeled training samples with a margin greater than a certain threshold. The pseudo-labeled examples are then used to enrich the labeled training data and train a new classifier in conjunction with the labeled training set. We present self-training methods for binary and multiclass classification and their variants which were recently developed using Neural Networks. Finally, we discuss our ideas for future research in self-training. To the best of our knowledge, this is the first thorough and complete survey on this subject.

Multi-class Probabilistic Bounds for Self-learning

Self-learning is a classical approach for learning with both labeled and unlabeled observations which consists in giving pseudo-labels to unlabeled training instances with a confidence score over a predetermined threshold. At the same time, the pseudo-labeling technique is prone to error and runs the risk of adding noisy labels into unlabeled training data. In this paper, we present a probabilistic framework for analyzing self-learning in the multi-class classification scenario with partially labeled data. First, we derive a transductive bound over the risk of the multi-class majority vote classifier. Based on this result, we propose to automatically choose the threshold for pseudo-labeling that minimizes the transductive bound. Then, we introduce a mislabeling error model to analyze the error of the majority vote classifier in the case of the pseudo-labeled data. We derive a probabilistic C-bound over the majority vote error when an imperfect label is given. Empirical results on different data sets show the effectiveness of our framework compared to several state-of-the-art semi-supervised approaches.

Semi-supervised Wrapper Feature Selection with Imperfect Labels

In this paper, we propose a new wrapper approach for semi-supervised feature selection. A common strategy in semi-supervised learning is to augment the training set by pseudo-labeled unlabeled examples. However, the pseudo-labeling procedure is prone to error and has a high risk of disrupting the learning algorithm with additional noisy labeled training data. To overcome this, we propose to model explicitly the mislabeling error during the learning phase with the overall aim of selecting the most relevant feature characteristics. We derive a $\mathcal{C}$-bound for Bayes classifiers trained over partially labeled training sets by taking into account the mislabeling errors. The risk bound is then considered as an objective function that is minimized over the space of possible feature subsets using a genetic algorithm. In order to produce both sparse and accurate solution, we propose a modification of a genetic algorithm with the crossover based on feature weights and recursive elimination of irrelevant features. Empirical results on different data sets show the effectiveness of our framework compared to several state-of-the-art semi-supervised feature selection approaches.