Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention

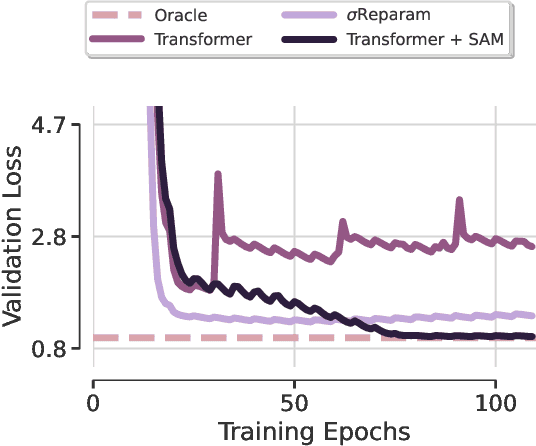
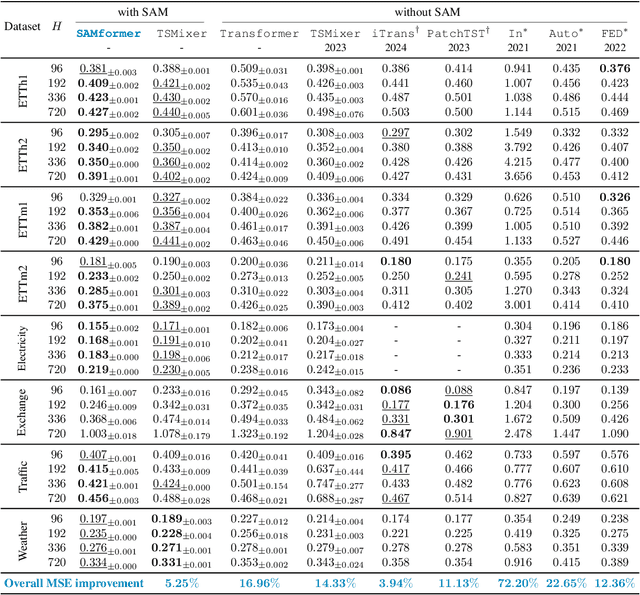
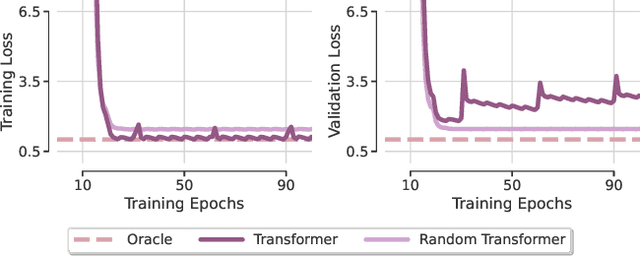
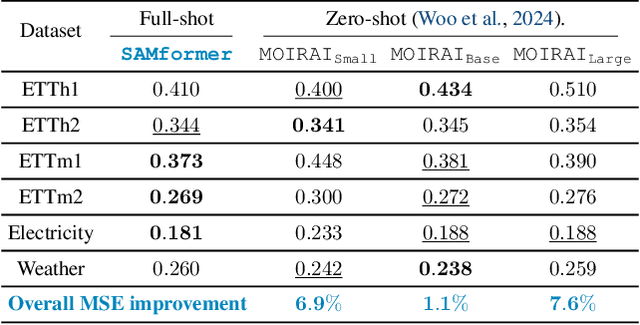
Transformer-based architectures achieved breakthrough performance in natural language processing and computer vision, yet they remain inferior to simpler linear baselines in multivariate long-term forecasting. To better understand this phenomenon, we start by studying a toy linear forecasting problem for which we show that transformers are incapable of converging to their true solution despite their high expressive power. We further identify the attention of transformers as being responsible for this low generalization capacity. Building upon this insight, we propose a shallow lightweight transformer model that successfully escapes bad local minima when optimized with sharpness-aware optimization. We empirically demonstrate that this result extends to all commonly used real-world multivariate time series datasets. In particular, SAMformer surpasses the current state-of-the-art model TSMixer by 14.33% on average, while having ~4 times fewer parameters. The code is available at https://github.com/romilbert/samformer.

Random Matrix Analysis to Balance between Supervised and Unsupervised Learning under the Low Density Separation Assumption

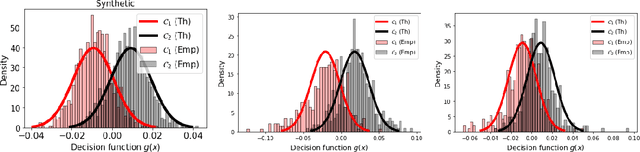
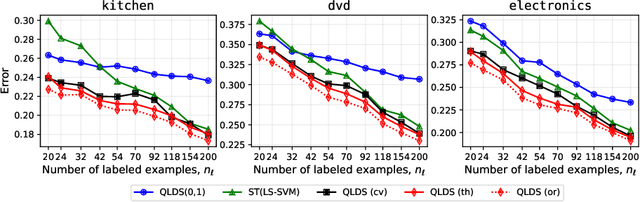
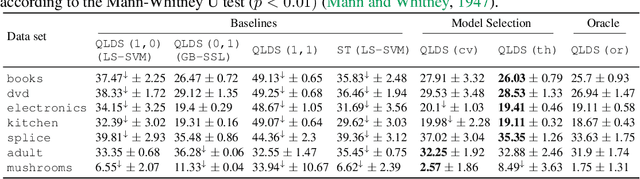
We propose a theoretical framework to analyze semi-supervised classification under the low density separation assumption in a high-dimensional regime. In particular, we introduce QLDS, a linear classification model, where the low density separation assumption is implemented via quadratic margin maximization. The algorithm has an explicit solution with rich theoretical properties, and we show that particular cases of our algorithm are the least-square support vector machine in the supervised case, the spectral clustering in the fully unsupervised regime, and a class of semi-supervised graph-based approaches. As such, QLDS establishes a smooth bridge between these supervised and unsupervised learning methods. Using recent advances in the random matrix theory, we formally derive a theoretical evaluation of the classification error in the asymptotic regime. As an application, we derive a hyperparameter selection policy that finds the best balance between the supervised and the unsupervised terms of our learning criterion. Finally, we provide extensive illustrations of our framework, as well as an experimental study on several benchmarks to demonstrate that QLDS, while being computationally more efficient, improves over cross-validation for hyperparameter selection, indicating a high promise of the usage of random matrix theory for semi-supervised model selection.

Knothe-Rosenblatt transport for Unsupervised Domain Adaptation

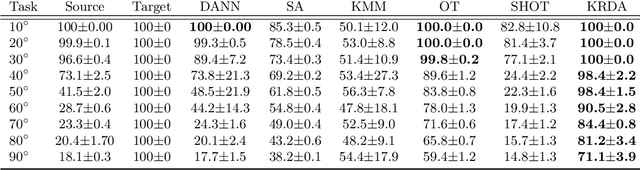
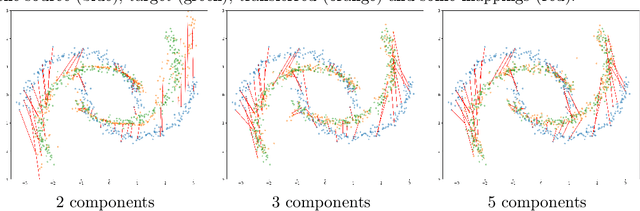
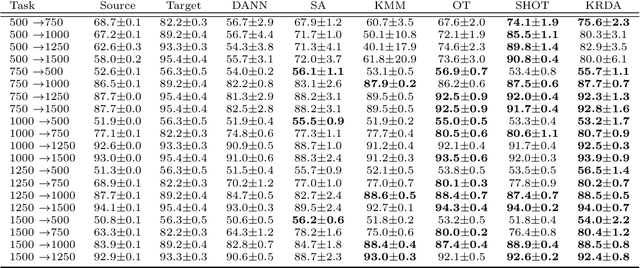
Unsupervised domain adaptation (UDA) aims at exploiting related but different data sources to tackle a common task in a target domain. UDA remains a central yet challenging problem in machine learning. In this paper, we present an approach tailored to moderate-dimensional tabular problems which are hugely important in industrial applications and less well-served by the plethora of methods designed for image and language data. Knothe-Rosenblatt Domain Adaptation (KRDA) is based on the Knothe-Rosenblatt transport: we exploit autoregressive density estimation algorithms to accurately model the different sources by an autoregressive model using a mixture of Gaussians. KRDA then takes advantage of the triangularity of the autoregressive models to build an explicit mapping of the source samples into the target domain. We show that the transfer map built by KRDA preserves each component quantiles of the observations, hence aligning the representations of the different data sets in the same target domain. Finally, we show that KRDA has state-of-the-art performance on both synthetic and real world UDA problems.

Lipschitz Normalization for Self-Attention Layers with Application to Graph Neural Networks

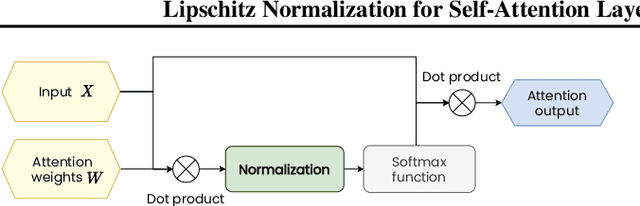
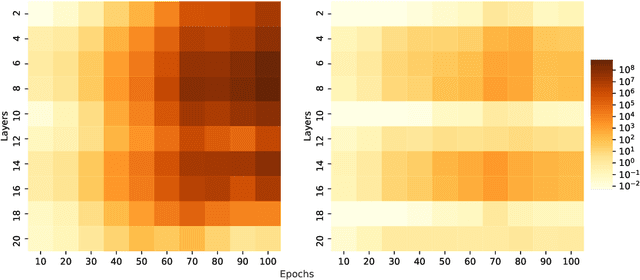
Attention based neural networks are state of the art in a large range of applications. However, their performance tends to degrade when the number of layers increases. In this work, we show that enforcing Lipschitz continuity by normalizing the attention scores can significantly improve the performance of deep attention models. First, we show that, for deep graph attention networks (GAT), gradient explosion appears during training, leading to poor performance of gradient-based training algorithms. To address this issue, we derive a theoretical analysis of the Lipschitz continuity of attention modules and introduce LipschitzNorm, a simple and parameter-free normalization for self-attention mechanisms that enforces the model to be Lipschitz continuous. We then apply LipschitzNorm to GAT and Graph Transformers and show that their performance is substantially improved in the deep setting (10 to 30 layers). More specifically, we show that a deep GAT model with LipschitzNorm achieves state of the art results for node label prediction tasks that exhibit long-range dependencies, while showing consistent improvements over their unnormalized counterparts in benchmark node classification tasks.

Improving Hierarchical Adversarial Robustness of Deep Neural Networks

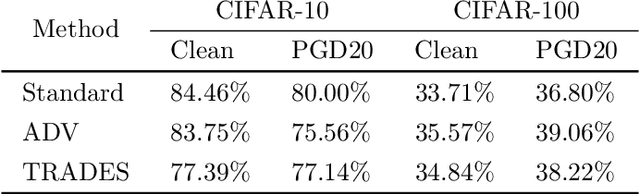
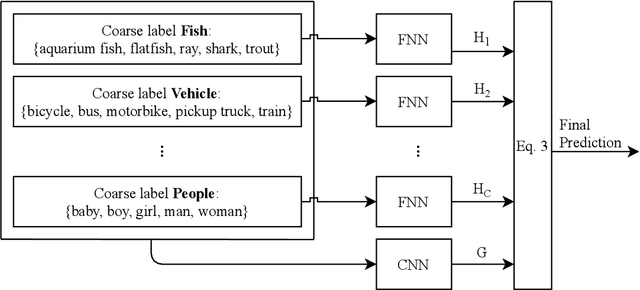
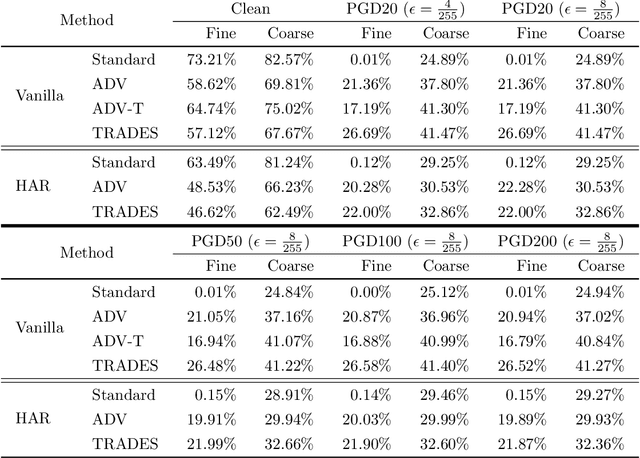
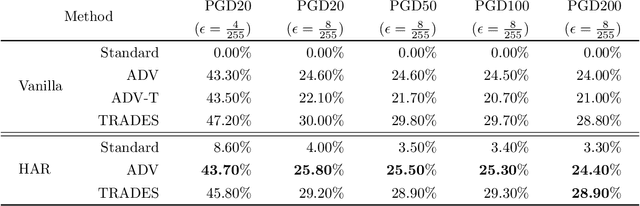
Do all adversarial examples have the same consequences? An autonomous driving system misclassifying a pedestrian as a car may induce a far more dangerous -- and even potentially lethal -- behavior than, for instance, a car as a bus. In order to better tackle this important problematic, we introduce the concept of hierarchical adversarial robustness. Given a dataset whose classes can be grouped into coarse-level labels, we define hierarchical adversarial examples as the ones leading to a misclassification at the coarse level. To improve the resistance of neural networks to hierarchical attacks, we introduce a hierarchical adversarially robust (HAR) network design that decomposes a single classification task into one coarse and multiple fine classification tasks, before being specifically trained by adversarial defense techniques. As an alternative to an end-to-end learning approach, we show that HAR significantly improves the robustness of the network against $\ell_2$ and $\ell_{\infty}$ bounded hierarchical attacks on the CIFAR-10 and CIFAR-100 dataset.

Ego-based Entropy Measures for Structural Representations on Graphs

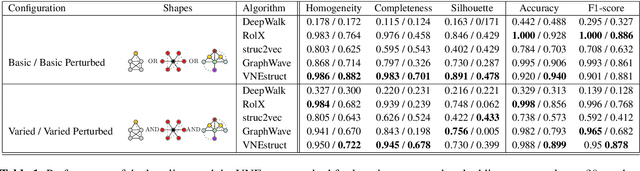
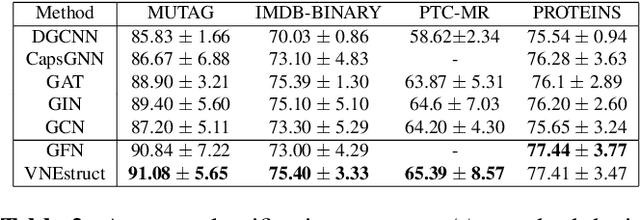
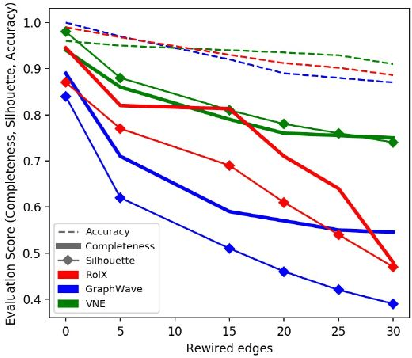
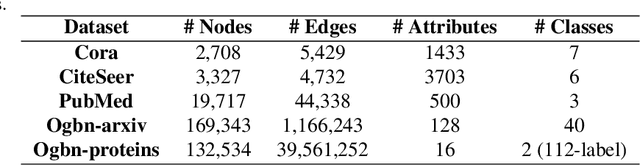
Machine learning on graph-structured data has attracted high research interest due to the emergence of Graph Neural Networks (GNNs). Most of the proposed GNNs are based on the node homophily, i.e neighboring nodes share similar characteristics. However, in many complex networks, nodes that lie to distant parts of the graph share structurally equivalent characteristics and exhibit similar roles (e.g chemical properties of distant atoms in a molecule, type of social network users). A growing literature proposed representations that identify structurally equivalent nodes. However, most of the existing methods require high time and space complexity. In this paper, we propose VNEstruct, a simple approach, based on entropy measures of the neighborhood's topology, for generating low-dimensional structural representations, that is time-efficient and robust to graph perturbations. Empirically, we observe that VNEstruct exhibits robustness on structural role identification tasks. Moreover, VNEstruct can achieve state-of-the-art performance on graph classification, without incorporating the graph structure information in the optimization, in contrast to GNN competitors.

Ego-based Entropy Measures for Structural Representations

In complex networks, nodes that share similar structural characteristics often exhibit similar roles (e.g type of users in a social network or the hierarchical position of employees in a company). In order to leverage this relationship, a growing literature proposed latent representations that identify structurally equivalent nodes. However, most of the existing methods require high time and space complexity. In this paper, we propose VNEstruct, a simple approach for generating low-dimensional structural node embeddings, that is both time efficient and robust to perturbations of the graph structure. The proposed approach focuses on the local neighborhood of each node and employs the Von Neumann entropy, an information-theoretic tool, to extract features that capture the neighborhood's topology. Moreover, on graph classification tasks, we suggest the utilization of the generated structural embeddings for the transformation of an attributed graph structure into a set of augmented node attributes. Empirically, we observe that the proposed approach exhibits robustness on structural role identification tasks and state-of-the-art performance on graph classification tasks, while maintaining very high computational speed.

Coloring graph neural networks for node disambiguation

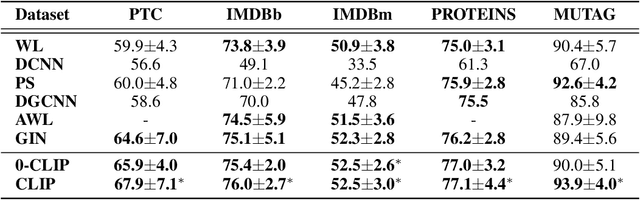
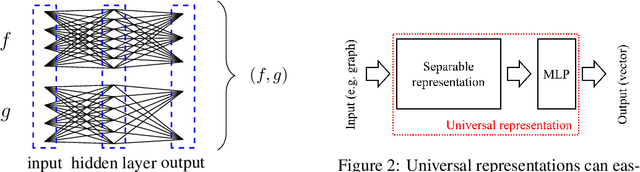
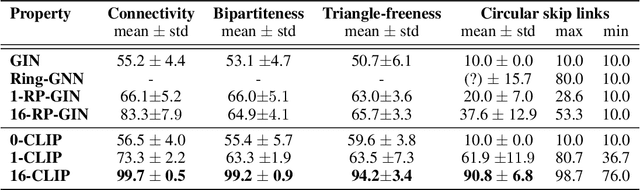
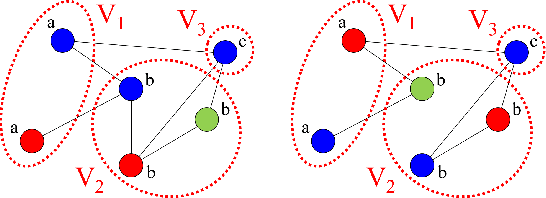
In this paper, we show that a simple coloring scheme can improve, both theoretically and empirically, the expressive power of Message Passing Neural Networks(MPNNs). More specifically, we introduce a graph neural network called Colored Local Iterative Procedure (CLIP) that uses colors to disambiguate identical node attributes, and show that this representation is a universal approximator of continuous functions on graphs with node attributes. Our method relies on separability , a key topological characteristic that allows to extend well-chosen neural networks into universal representations. Finally, we show experimentally that CLIP is capable of capturing structural characteristics that traditional MPNNs fail to distinguish,while being state-of-the-art on benchmark graph classification datasets.

Lipschitz regularity of deep neural networks: analysis and efficient estimation

Deep neural networks are notorious for being sensitive to small well-chosen perturbations, and estimating the regularity of such architectures is of utmost importance for safe and robust practical applications. In this paper, we investigate one of the key characteristics to assess the regularity of such methods: the Lipschitz constant of deep learning architectures. First, we show that, even for two layer neural networks, the exact computation of this quantity is NP-hard and state-of-art methods may significantly overestimate it. Then, we both extend and improve previous estimation methods by providing AutoLip, the first generic algorithm for upper bounding the Lipschitz constant of any automatically differentiable function. We provide a power method algorithm working with automatic differentiation, allowing efficient computations even on large convolutions. Second, for sequential neural networks, we propose an improved algorithm named SeqLip that takes advantage of the linear computation graph to split the computation per pair of consecutive layers. Third we propose heuristics on SeqLip in order to tackle very large networks. Our experiments show that SeqLip can significantly improve on the existing upper bounds.