Universal Scale Laws for Colors and Patterns in Imagery

Distribution of colors and patterns in images is observed through cascades that adjust spatial resolution and dynamics. Cascades of colors reveal the emergent universal property that Fully Colored Images (FCIs) of natural scenes adhere to the debated continuous linear log-scale law (slope $-2.00 \pm 0.01$) (L1). Cascades of discrete $2 \times 2$ patterns are derived from pixel squares reductions onto the seven unlabeled rotation-free textures (0000, 0001, 0011, 0012, 0101, 0102, 0123). They exhibit an unparalleled universal entropy maximum of $1.74 \pm 0.013$ at some dynamics regardless of spatial scale (L2). Patterns also adhere to the Integral Fluctuation Theorem ($1.00 \pm 0.01$) (L3), pivotal in studies of chaotic systems. Images with fewer colors exhibit quadratic shift and bias from L1 and L3 but adhere to L2. Randomized Hilbert fractals FCIs better match the laws than basic-to-AI-based simulations. Those results are of interest in Neural Networks, out of equilibrium physics and spectral imagery.

Universal Robustness via Median Randomized Smoothing for Real-World Super-Resolution

Most of the recent literature on image Super-Resolution (SR) can be classified into two main approaches. The first one involves learning a corruption model tailored to a specific dataset, aiming to mimic the noise and corruption in low-resolution images, such as sensor noise. However, this approach is data-specific, tends to lack adaptability, and its accuracy diminishes when faced with unseen types of image corruptions. A second and more recent approach, referred to as Robust Super-Resolution (RSR), proposes to improve real-world SR by harnessing the generalization capabilities of a model by making it robust to adversarial attacks. To delve further into this second approach, our paper explores the universality of various methods for enhancing the robustness of deep learning SR models. In other words, we inquire: "Which robustness method exhibits the highest degree of adaptability when dealing with a wide range of adversarial attacks ?". Our extensive experimentation on both synthetic and real-world images empirically demonstrates that median randomized smoothing (MRS) is more general in terms of robustness compared to adversarial learning techniques, which tend to focus on specific types of attacks. Furthermore, as expected, we also illustrate that the proposed universal robust method enables the SR model to handle standard corruptions more effectively, such as blur and Gaussian noise, and notably, corruptions naturally present in real-world images. These results support the significance of shifting the paradigm in the development of real-world SR methods towards RSR, especially via MRS.

EpipolarNVS: leveraging on Epipolar geometry for single-image Novel View Synthesis

Novel-view synthesis (NVS) can be tackled through different approaches, depending on the general setting: a single source image to a short video sequence, exact or noisy camera pose information, 3D-based information such as point clouds etc. The most challenging scenario, the one where we stand in this work, only considers a unique source image to generate a novel one from another viewpoint. However, in such a tricky situation, the latest learning-based solutions often struggle to integrate the camera viewpoint transformation. Indeed, the extrinsic information is often passed as-is, through a low-dimensional vector. It might even occur that such a camera pose, when parametrized as Euler angles, is quantized through a one-hot representation. This vanilla encoding choice prevents the learnt architecture from inferring novel views on a continuous basis (from a camera pose perspective). We claim it exists an elegant way to better encode relative camera pose, by leveraging 3D-related concepts such as the epipolar constraint. We, therefore, introduce an innovative method that encodes the viewpoint transformation as a 2D feature image. Such a camera encoding strategy gives meaningful insights to the network regarding how the camera has moved in space between the two views. By encoding the camera pose information as a finite number of coloured epipolar lines, we demonstrate through our experiments that our strategy outperforms vanilla encoding.

Pruning-based Topology Refinement of 3D Mesh using a 2D Alpha Mask

Image-based 3D reconstruction has increasingly stunning results over the past few years with the latest improvements in computer vision and graphics. Geometry and topology are two fundamental concepts when dealing with 3D mesh structures. But the latest often remains a side issue in the 3D mesh-based reconstruction literature. Indeed, performing per-vertex elementary displacements over a 3D sphere mesh only impacts its geometry and leaves the topological structure unchanged and fixed. Whereas few attempts propose to update the geometry and the topology, all need to lean on costly 3D ground-truth to determine the faces/edges to prune. We present in this work a method that aims to refine the topology of any 3D mesh through a face-pruning strategy that extensively relies upon 2D alpha masks and camera pose information. Our solution leverages a differentiable renderer that renders each face as a 2D soft map. Its pixel intensity reflects the probability of being covered during the rendering process by such a face. Based on the 2D soft-masks available, our method is thus able to quickly highlight all the incorrectly rendered faces for a given viewpoint. Because our module is agnostic to the network that produces the 3D mesh, it can be easily plugged into any self-supervised image-based (either synthetic or natural) 3D reconstruction pipeline to get complex meshes with a non-spherical topology.

Self-Improving SLAM in Dynamic Environments: Learning When to Mask

Visual SLAM -- Simultaneous Localization and Mapping -- in dynamic environments typically relies on identifying and masking image features on moving objects to prevent them from negatively affecting performance. Current approaches are suboptimal: they either fail to mask objects when needed or, on the contrary, mask objects needlessly. Thus, we propose a novel SLAM that learns when masking objects improves its performance in dynamic scenarios. Given a method to segment objects and a SLAM, we give the latter the ability of Temporal Masking, i.e., to infer when certain classes of objects should be masked to maximize any given SLAM metric. We do not make any priors on motion: our method learns to mask moving objects by itself. To prevent high annotations costs, we created an automatic annotation method for self-supervised training. We constructed a new dataset, named ConsInv, which includes challenging real-world dynamic sequences respectively indoors and outdoors. Our method reaches the state of the art on the TUM RGB-D dataset and outperforms it on KITTI and ConsInv datasets.

Trustworthiness of Laser-Induced Breakdown Spectroscopy Predictions via Simulation-based Synthetic Data Augmentation and Multitask Learning

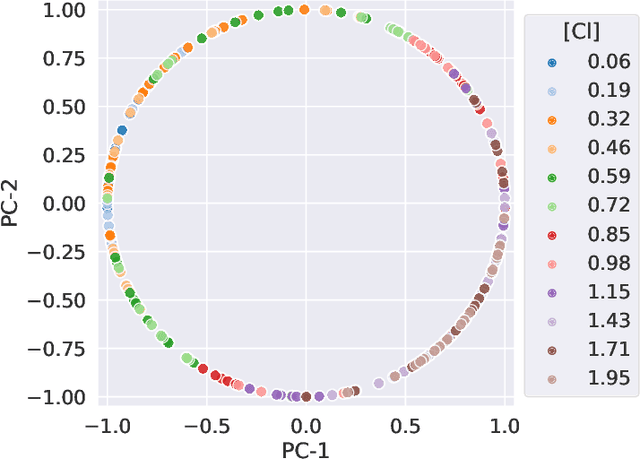
We consider quantitative analyses of spectral data using laser-induced breakdown spectroscopy. We address the small size of training data available, and the validation of the predictions during inference on unknown data. For the purpose, we build robust calibration models using deep convolutional multitask learning architectures to predict the concentration of the analyte, alongside additional spectral information as auxiliary outputs. These secondary predictions can be used to validate the trustworthiness of the model by taking advantage of the mutual dependencies of the parameters of the multitask neural networks. Due to the experimental lack of training samples, we introduce a simulation-based data augmentation process to synthesise an arbitrary number of spectra, statistically representative of the experimental data. Given the nature of the deep learning model, no dimensionality reduction or data selection processes are required. The procedure is an end-to-end pipeline including the process of synthetic data augmentation, the construction of a suitable robust, homoscedastic, deep learning model, and the validation of its predictions. In the article, we compare the performance of the multitask model with traditional univariate and multivariate analyses, to highlight the separate contributions of each element introduced in the process.

Selective Multiple Power Iteration: from Tensor PCA to gradient-based exploration of landscapes

We propose Selective Multiple Power Iterations (SMPI), a new algorithm to address the important Tensor PCA problem that consists in recovering a spike $\bf{v_0}^{\otimes k}$ corrupted by a Gaussian noise tensor $\bf{Z} \in (\mathbb{R}^n)^{\otimes k}$ such that $\bf{T}=\sqrt{n} \beta \bf{v_0}^{\otimes k} + \bf{Z}$ where $\beta$ is the signal-to-noise ratio (SNR). SMPI consists in generating a polynomial number of random initializations, performing a polynomial number of symmetrized tensor power iterations on each initialization, then selecting the one that maximizes $\langle \bf{T}, \bf{v}^{\otimes k} \rangle$. Various numerical simulations for $k=3$ in the conventionally considered range $n \leq 1000$ show that the experimental performances of SMPI improve drastically upon existent algorithms and becomes comparable to the theoretical optimal recovery. We show that these unexpected performances are due to a powerful mechanism in which the noise plays a key role for the signal recovery and that takes place at low $\beta$. Furthermore, this mechanism results from five essential features of SMPI that distinguish it from previous algorithms based on power iteration. These remarkable results may have strong impact on both practical and theoretical applications of Tensor PCA. (i) We provide a variant of this algorithm to tackle low-rank CP tensor decomposition. These proposed algorithms also outperforms existent methods even on real data which shows a huge potential impact for practical applications. (ii) We present new theoretical insights on the behavior of SMPI and gradient descent methods for the optimization in high-dimensional non-convex landscapes that are present in various machine learning problems. (iii) We expect that these results may help the discussion concerning the existence of the conjectured statistical-algorithmic gap.

HyperPCA: a Powerful Tool to Extract Elemental Maps from Noisy Data Obtained in LIBS Mapping of Materials

Laser-induced breakdown spectroscopy is a preferred technique for fast and direct multi-elemental mapping of samples under ambient pressure, without any limitation on the targeted element. However, LIBS mapping data have two peculiarities: an intrinsically low signal-to-noise ratio due to single-shot measurements, and a high dimensionality due to the high number of spectra acquired for imaging. This is all the truer as lateral resolution gets higher: in this case, the ablation spot diameter is reduced, as well as the ablated mass and the emission signal, while the number of spectra for a given surface increases. Therefore, efficient extraction of physico-chemical information from a noisy and large dataset is a major issue. Multivariate approaches were introduced by several authors as a means to cope with such data, particularly Principal Component Analysis. Yet, PCA is known to present theoretical constraints for the consistent reconstruction of the dataset, and has therefore limitations to efficient interpretation of LIBS mapping data. In this paper, we introduce HyperPCA, a new analysis tool for hyperspectral images based on a sparse representation of the data using Discrete Wavelet Transform and kernel-based sparse PCA to reduce the impact of noise on the data and to consistently reconstruct the spectroscopic signal, with a particular emphasis on LIBS data. The method is first illustrated using simulated LIBS mapping datasets to emphasize its performances with highly noisy and/or highly interfered spectra. Comparisons to standard PCA and to traditional univariate data analyses are provided. Finally, it is used to process real data in two cases that clearly illustrate the potential of the proposed algorithm. We show that the method presents advantages both in quantity and quality of the information recovered, thus improving the physico-chemical characterisation of analysed surfaces.

A Multiple-View Geometric Model for Specularity Prediction on Non-Uniformly Curved Surfaces

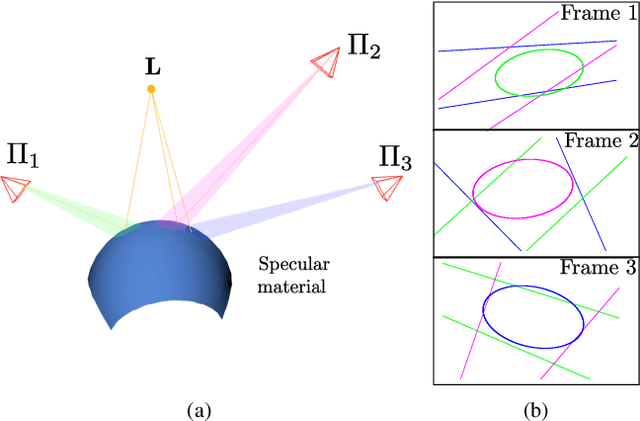
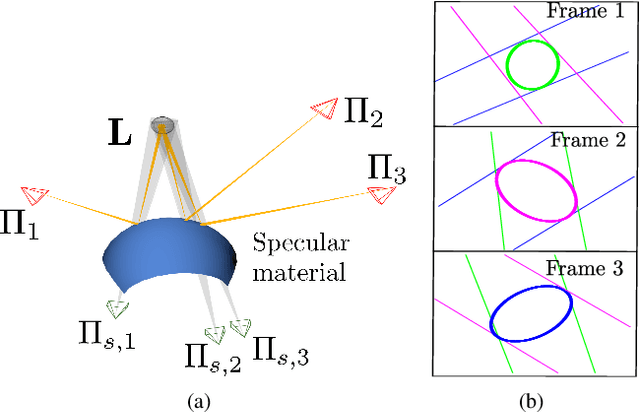
Specularity prediction is essential to many computer vision applications by giving important visual cues that could be used in Augmented Reality (AR), Simultaneous Localisation and Mapping (SLAM), 3D reconstruction and material modeling, thus improving scene understanding. However, it is a challenging task requiring numerous information from the scene including the camera pose, the geometry of the scene, the light sources and the material properties. Our previous work have addressed this task by creating an explicit model using an ellipsoid whose projection fits the specularity image contours for a given camera pose. These ellipsoid-based approaches belong to a family of models called JOint-LIght MAterial Specularity (JOLIMAS), where we have attempted to gradually remove assumptions on the scene such as the geometry of the specular surfaces. However, our most recent approach is still limited to uniformly curved surfaces. This paper builds upon these methods by generalising JOLIMAS to any surface geometry while improving the quality of specularity prediction, without sacrificing computation performances. The proposed method establishes a link between surface curvature and specularity shape in order to lift the geometric assumptions from previous work. Contrary to previous work, our new model is built from a physics-based local illumination model namely Torrance-Sparrow, providing a better model reconstruction. Specularity prediction using our new model is tested against the most recent JOLIMAS version on both synthetic and real sequences with objects of varying shape curvatures. Our method outperforms previous approaches in specularity prediction, including the real-time setup, as shown in the supplementary material using videos.

Deep multi-task mining Calabi-Yau four-folds

We continue earlier efforts in computing the dimensions of tangent space cohomologies of Calabi-Yau manifolds using deep learning. In this paper, we consider the dataset of all Calabi-Yau four-folds constructed as complete intersections in products of projective spaces. Employing neural networks inspired by state-of-the-art computer vision architectures, we improve earlier benchmarks and demonstrate that all four non-trivial Hodge numbers can be learned at the same time using a multi-task architecture. With 30% (80%) training ratio, we reach an accuracy of 100% for $h^{(1,1)}$ and 97% for $h^{(2,1)}$ (100% for both), 81% (96%) for $h^{(3,1)}$, and 49% (83%) for $h^{(2,2)}$. Assuming that the Euler number is known, as it is easy to compute, and taking into account the linear constraint arising from index computations, we get 100% total accuracy.