An objective comparison of methods for augmented reality in laparoscopic liver resection by preoperative-to-intraoperative image fusion

Augmented reality for laparoscopic liver resection is a visualisation mode that allows a surgeon to localise tumours and vessels embedded within the liver by projecting them on top of a laparoscopic image. Preoperative 3D models extracted from CT or MRI data are registered to the intraoperative laparoscopic images during this process. In terms of 3D-2D fusion, most of the algorithms make use of anatomical landmarks to guide registration. These landmarks include the liver's inferior ridge, the falciform ligament, and the occluding contours. They are usually marked by hand in both the laparoscopic image and the 3D model, which is time-consuming and may contain errors if done by a non-experienced user. Therefore, there is a need to automate this process so that augmented reality can be used effectively in the operating room. We present the Preoperative-to-Intraoperative Laparoscopic Fusion Challenge (P2ILF), held during the Medical Imaging and Computer Assisted Interventions (MICCAI 2022) conference, which investigates the possibilities of detecting these landmarks automatically and using them in registration. The challenge was divided into two tasks: 1) A 2D and 3D landmark detection task and 2) a 3D-2D registration task. The teams were provided with training data consisting of 167 laparoscopic images and 9 preoperative 3D models from 9 patients, with the corresponding 2D and 3D landmark annotations. A total of 6 teams from 4 countries participated, whose proposed methods were evaluated on 16 images and two preoperative 3D models from two patients. All the teams proposed deep learning-based methods for the 2D and 3D landmark segmentation tasks and differentiable rendering-based methods for the registration task. Based on the experimental outcomes, we propose three key hypotheses that determine current limitations and future directions for research in this domain.

Reconstructing the normal and shape at specularities in endoscopy

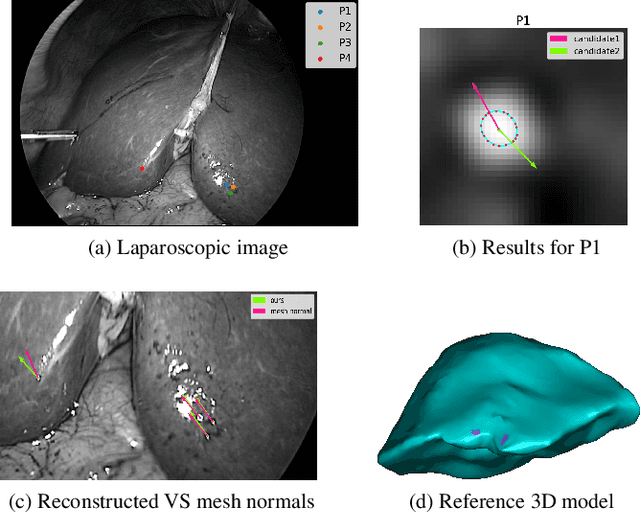
Specularities are numerous in endoscopic images. They occur as many white small elliptic spots, which are generally ruled out as nuisance in image analysis and computer vision methods. Instead, we propose to use specularities as cues for 3D perception. Specifically, we propose a new method to reconstruct, at each specularity, the observed tissue's normal direction (i.e., its orientation) and shape (i.e., its curvature) from a single image. We show results on simulated and real interventional images.

KernelGPA: A Globally Optimal Solution to Deformable SLAM in Closed-form

We study the generalized Procrustes analysis (GPA), as a minimal formulation to the simultaneous localization and mapping (SLAM) problem. We propose KernelGPA, a novel global registration technique to solve SLAM in the deformable environment. We propose the concept of deformable transformation which encodes the entangled pose and deformation. We define deformable transformations using a kernel method, and show that both the deformable transformations and the environment map can be solved globally in closed-form, up to global scale ambiguities. We solve the scale ambiguities by an optimization formulation that maximizes rigidity. We demonstrate KernelGPA using the Gaussian kernel, and validate the superiority of KernelGPA with various datasets. Code and data are available at \url{https://bitbucket.org/FangBai/deformableprocrustes}.

Freehand 2D Ultrasound Probe Calibration for Image Fusion with 3D MRI/CT

The aim of this work is to implement a simple freehand ultrasound (US) probe calibration technique. This will enable us to visualize US image data during surgical procedures using augmented reality. The performance of the system was evaluated with different experiments using two different pose estimation techniques. A near-millimeter accuracy can be achieved with the proposed approach. The developed system is cost-effective, simple and rapid with low calibration error

ROBUSfT: Robust Real-Time Shape-from-Template, a C++ Library

Tracking the 3D shape of a deforming object using only monocular 2D vision is a challenging problem. This is because one should (i) infer the 3D shape from a 2D image, which is a severely underconstrained problem, and (ii) implement the whole solution pipeline in real-time. The pipeline typically requires feature detection and matching, mismatch filtering, 3D shape inference and feature tracking algorithms. We propose ROBUSfT, a conventional pipeline based on a template containing the object's rest shape, texturemap and deformation law. ROBUSfT is ready-to-use, wide-baseline, capable of handling large deformations, fast up to 30 fps, free of training, and robust against partial occlusions and discontinuity in video frames. It outperforms the state-of-the-art methods in challenging datasets. ROBUSfT is implemented as a publicly available C++ library and we provide a tutorial on how to use it in https://github.com/mrshetab/ROBUSfT

Convex Relaxations for Isometric and Equiareal NRSfM

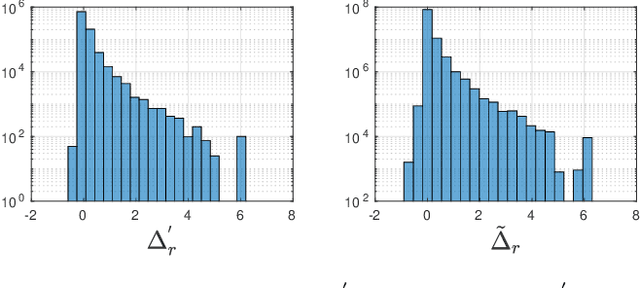
Extensible objects form a challenging case for NRSfM, owing to the lack of a sufficiently constrained extensible model of the point-cloud. We tackle the challenge by proposing 1) convex relaxations of the isometric model up to quasi-isometry, and 2) convex relaxations involving the equiareal deformation model, which preserves local area and has not been used in NRSfM. The equiareal model is appealing because it is physically plausible and widely applicable. However, it has two main difficulties: first, when used on its own, it is ambiguous, and second, it involves quartic, hence highly nonconvex, constraints. Our approach handles the first difficulty by mixing the equiareal with the isometric model and the second difficulty by new convex relaxations. We validate our methods on multiple real and synthetic data, including well-known benchmarks.

Normal reconstruction from specularity in the endoscopic setting

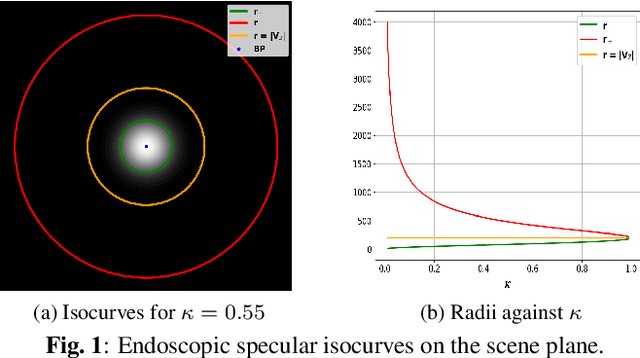
We show that for a plane imaged by an endoscope the specular isophotes are concentric circles on the scene plane, which appear as nested ellipses in the image. We show that these ellipses can be detected and used to estimate the plane's normal direction, forming a normal reconstruction method, which we validate on simulated data. In practice, the anatomical surfaces visible in endoscopic images are locally planar. We use our method to show that the surface normal can thus be reconstructed for each of the numerous specularities typically visible on moist tissues. We show results on laparoscopic and colonoscopic images.

The Proxy Step-size Technique for Regularized Optimization on the Sphere Manifold

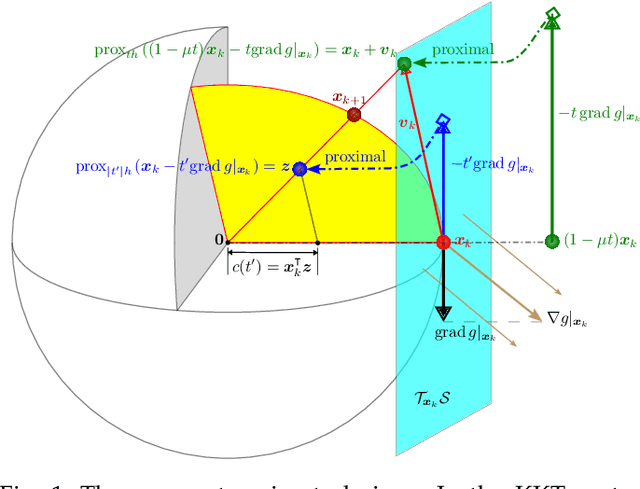
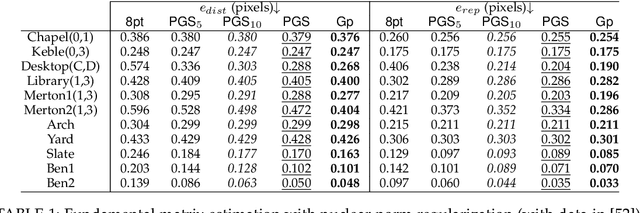
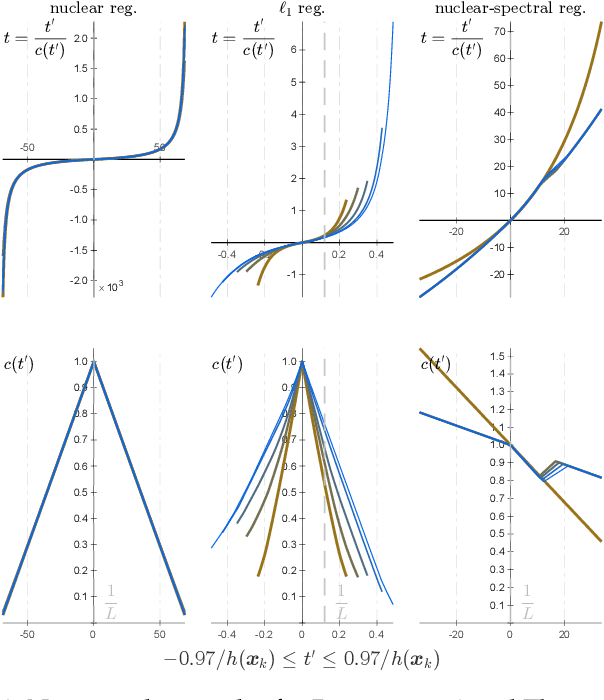
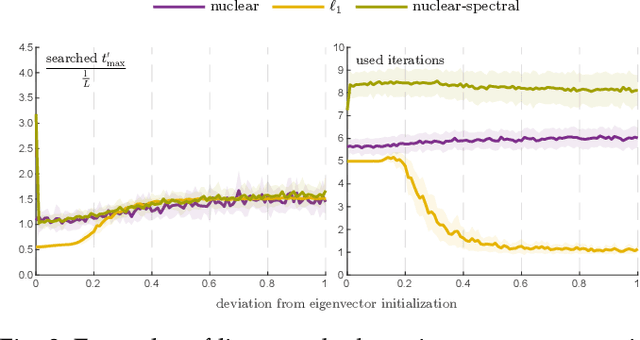
We give an effective solution to the regularized optimization problem $g (\boldsymbol{x}) + h (\boldsymbol{x})$, where $\boldsymbol{x}$ is constrained on the unit sphere $\Vert \boldsymbol{x} \Vert_2 = 1$. Here $g (\cdot)$ is a smooth cost with Lipschitz continuous gradient within the unit ball $\{\boldsymbol{x} : \Vert \boldsymbol{x} \Vert_2 \le 1 \}$ whereas $h (\cdot)$ is typically non-smooth but convex and absolutely homogeneous, \textit{e.g.,}~norm regularizers and their combinations. Our solution is based on the Riemannian proximal gradient, using an idea we call \textit{proxy step-size} -- a scalar variable which we prove is monotone with respect to the actual step-size within an interval. The proxy step-size exists ubiquitously for convex and absolutely homogeneous $h(\cdot)$, and decides the actual step-size and the tangent update in closed-form, thus the complete proximal gradient iteration. Based on these insights, we design a Riemannian proximal gradient method using the proxy step-size. We prove that our method converges to a critical point, guided by a line-search technique based on the $g(\cdot)$ cost only. The proposed method can be implemented in a couple of lines of code. We show its usefulness by applying nuclear norm, $\ell_1$ norm, and nuclear-spectral norm regularization to three classical computer vision problems. The improvements are consistent and backed by numerical experiments.

Procrustes Analysis with Deformations: A Closed-Form Solution by Eigenvalue Decomposition

Generalized Procrustes Analysis (GPA) is the problem of bringing multiple shapes into a common reference by estimating transformations. GPA has been extensively studied for the Euclidean and affine transformations. We introduce GPA with deformable transformations, which forms a much wider and difficult problem. We specifically study a class of transformations called the Linear Basis Warps (LBWs), which contains the affine transformation and most of the usual deformation models, such as the Thin-Plate Spline (TPS). GPA with deformations is a nonconvex underconstrained problem. We resolve the fundamental ambiguities of deformable GPA using two shape constraints requiring the eigenvalues of the shape covariance. These eigenvalues can be computed independently as a prior or posterior. We give a closed-form and optimal solution to deformable GPA based on an eigenvalue decomposition. This solution handles regularization, favoring smooth deformation fields. It requires the transformation model to satisfy a fundamental property of free-translations, which asserts that the model can implement any translation. We show that this property fortunately holds true for most common transformation models, including the affine and TPS models. For the other models, we give another closed-form solution to GPA, which agrees exactly with the first solution for models with free-translation. We give pseudo-code for computing our solution, leading to the proposed DefGPA method, which is fast, globally optimal and widely applicable. We validate our method and compare it to previous work on six diverse 2D and 3D datasets, with special care taken to choose the hyperparameters from cross-validation.

A Multiple-View Geometric Model for Specularity Prediction on Non-Uniformly Curved Surfaces

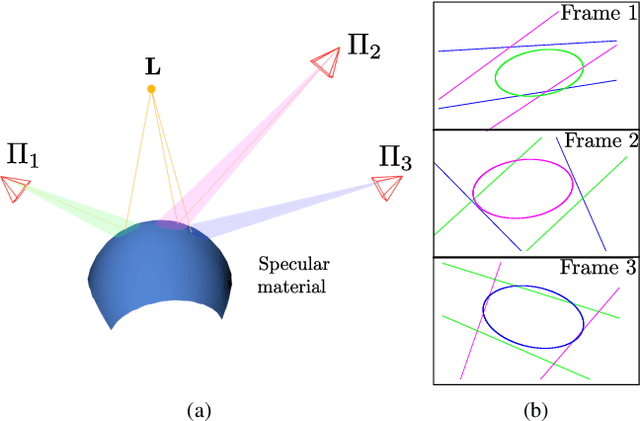
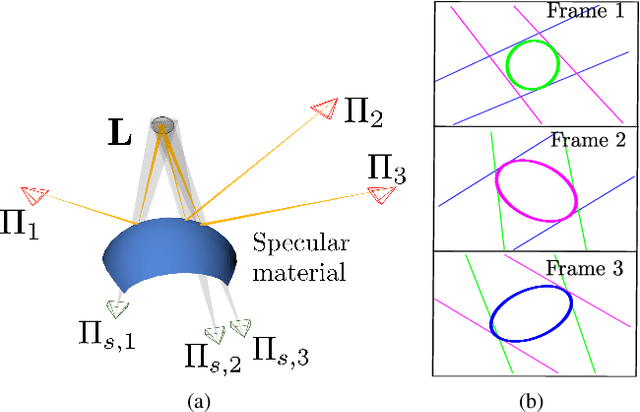
Specularity prediction is essential to many computer vision applications by giving important visual cues that could be used in Augmented Reality (AR), Simultaneous Localisation and Mapping (SLAM), 3D reconstruction and material modeling, thus improving scene understanding. However, it is a challenging task requiring numerous information from the scene including the camera pose, the geometry of the scene, the light sources and the material properties. Our previous work have addressed this task by creating an explicit model using an ellipsoid whose projection fits the specularity image contours for a given camera pose. These ellipsoid-based approaches belong to a family of models called JOint-LIght MAterial Specularity (JOLIMAS), where we have attempted to gradually remove assumptions on the scene such as the geometry of the specular surfaces. However, our most recent approach is still limited to uniformly curved surfaces. This paper builds upon these methods by generalising JOLIMAS to any surface geometry while improving the quality of specularity prediction, without sacrificing computation performances. The proposed method establishes a link between surface curvature and specularity shape in order to lift the geometric assumptions from previous work. Contrary to previous work, our new model is built from a physics-based local illumination model namely Torrance-Sparrow, providing a better model reconstruction. Specularity prediction using our new model is tested against the most recent JOLIMAS version on both synthetic and real sequences with objects of varying shape curvatures. Our method outperforms previous approaches in specularity prediction, including the real-time setup, as shown in the supplementary material using videos.