Fang Bai
KernelGPA: A Globally Optimal Solution to Deformable SLAM in Closed-form
Oct 28, 2023Abstract:We study the generalized Procrustes analysis (GPA), as a minimal formulation to the simultaneous localization and mapping (SLAM) problem. We propose KernelGPA, a novel global registration technique to solve SLAM in the deformable environment. We propose the concept of deformable transformation which encodes the entangled pose and deformation. We define deformable transformations using a kernel method, and show that both the deformable transformations and the environment map can be solved globally in closed-form, up to global scale ambiguities. We solve the scale ambiguities by an optimization formulation that maximizes rigidity. We demonstrate KernelGPA using the Gaussian kernel, and validate the superiority of KernelGPA with various datasets. Code and data are available at \url{https://bitbucket.org/FangBai/deformableprocrustes}.
* This paper has been accepted for publication in the International Journal of Robotics Research, 2023. https://doi.org/10.1177/02783649231195380
The Proxy Step-size Technique for Regularized Optimization on the Sphere Manifold
Sep 05, 2022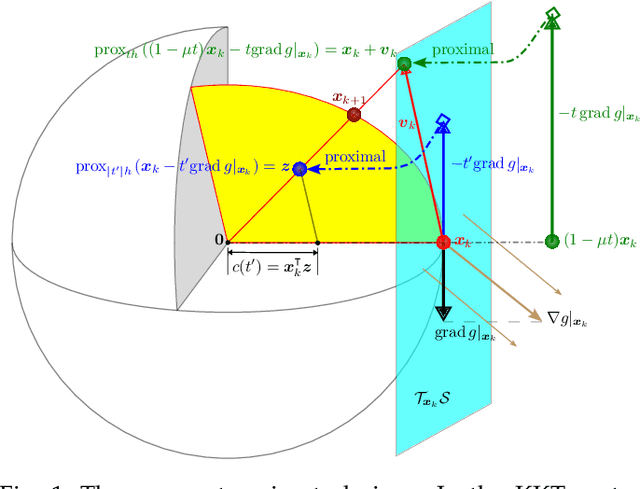
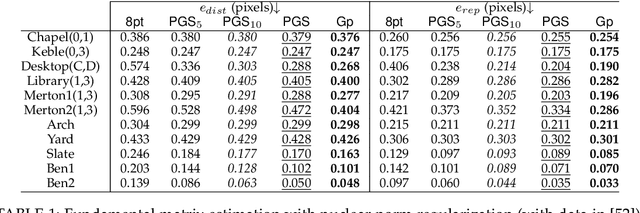
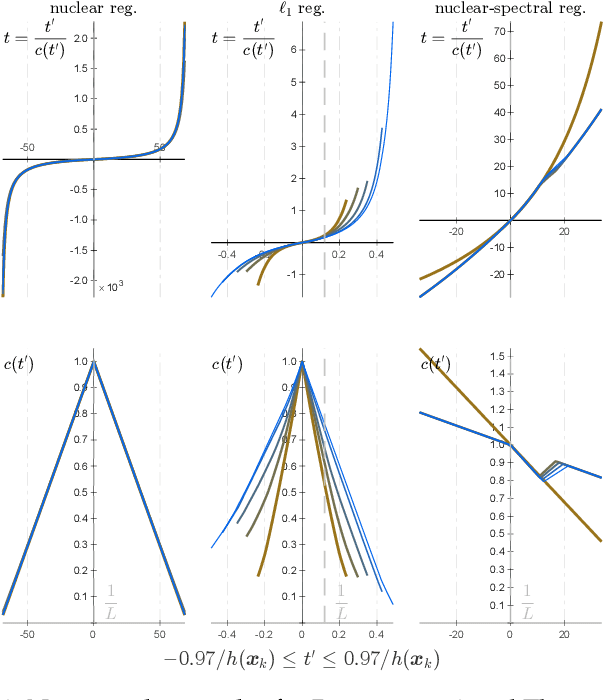
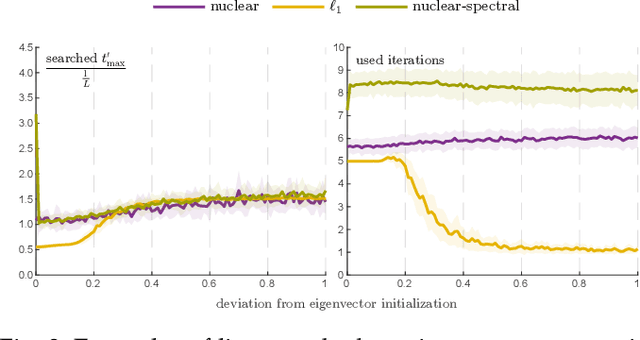
Abstract:We give an effective solution to the regularized optimization problem $g (\boldsymbol{x}) + h (\boldsymbol{x})$, where $\boldsymbol{x}$ is constrained on the unit sphere $\Vert \boldsymbol{x} \Vert_2 = 1$. Here $g (\cdot)$ is a smooth cost with Lipschitz continuous gradient within the unit ball $\{\boldsymbol{x} : \Vert \boldsymbol{x} \Vert_2 \le 1 \}$ whereas $h (\cdot)$ is typically non-smooth but convex and absolutely homogeneous, \textit{e.g.,}~norm regularizers and their combinations. Our solution is based on the Riemannian proximal gradient, using an idea we call \textit{proxy step-size} -- a scalar variable which we prove is monotone with respect to the actual step-size within an interval. The proxy step-size exists ubiquitously for convex and absolutely homogeneous $h(\cdot)$, and decides the actual step-size and the tangent update in closed-form, thus the complete proximal gradient iteration. Based on these insights, we design a Riemannian proximal gradient method using the proxy step-size. We prove that our method converges to a critical point, guided by a line-search technique based on the $g(\cdot)$ cost only. The proposed method can be implemented in a couple of lines of code. We show its usefulness by applying nuclear norm, $\ell_1$ norm, and nuclear-spectral norm regularization to three classical computer vision problems. The improvements are consistent and backed by numerical experiments.
Procrustes Analysis with Deformations: A Closed-Form Solution by Eigenvalue Decomposition
Jun 29, 2022Abstract:Generalized Procrustes Analysis (GPA) is the problem of bringing multiple shapes into a common reference by estimating transformations. GPA has been extensively studied for the Euclidean and affine transformations. We introduce GPA with deformable transformations, which forms a much wider and difficult problem. We specifically study a class of transformations called the Linear Basis Warps (LBWs), which contains the affine transformation and most of the usual deformation models, such as the Thin-Plate Spline (TPS). GPA with deformations is a nonconvex underconstrained problem. We resolve the fundamental ambiguities of deformable GPA using two shape constraints requiring the eigenvalues of the shape covariance. These eigenvalues can be computed independently as a prior or posterior. We give a closed-form and optimal solution to deformable GPA based on an eigenvalue decomposition. This solution handles regularization, favoring smooth deformation fields. It requires the transformation model to satisfy a fundamental property of free-translations, which asserts that the model can implement any translation. We show that this property fortunately holds true for most common transformation models, including the affine and TPS models. For the other models, we give another closed-form solution to GPA, which agrees exactly with the first solution for models with free-translation. We give pseudo-code for computing our solution, leading to the proposed DefGPA method, which is fast, globally optimal and widely applicable. We validate our method and compare it to previous work on six diverse 2D and 3D datasets, with special care taken to choose the hyperparameters from cross-validation.
* Published on International journal of computer vision (IJCV) 2022
Change of Optimal Values: A Pre-calculated Metric
Jun 23, 2022



Abstract:A variety of optimization problems takes the form of a minimum norm optimization. In this paper, we study the change of optimal values between two incrementally constructed least norm optimization problems, with new measurements included in the second one. We prove an exact equation to calculate the change of optimal values in the linear least norm optimization problem. With the result in this paper, the change of the optimal values can be pre-calculated as a metric to guide online decision makings, without solving the second optimization problem as long the solution and covariance of the first optimization problem are available. The result can be extended to linear least distance optimization problems, and nonlinear least distance optimization with (nonlinear) equality constraints through linearizations. This derivation in this paper provides a theoretically sound explanation to the empirical observations shown in RA-L 2018 bai et al. As an additional contribution, we propose another optimization problem, i.e. aligning two trajectories at given poses, to further demonstrate how to use the metric. The accuracy of the metric is validated with numerical examples, which is quite satisfactory in general (see the experiments in RA-L 2018 bai et al.} as well), unless in some extremely adverse scenarios. Last but not least, calculating the optimal value by the proposed metric is at least one magnitude faster than solving the corresponding optimization problems directly.
* 6 pages on IEEE International Conference on Robotics and Automation (ICRA), 2020
Sparse Pose Graph Optimization in Cycle Space
Mar 29, 2022



Abstract:The state-of-the-art modern pose-graph optimization (PGO) systems are vertex based. In this context the number of variables might be high, albeit the number of cycles in the graph (loop closures) is relatively low. For sparse problems particularly, the cycle space has a significantly smaller dimension than the number of vertices. By exploiting this observation, in this paper we propose an alternative solution to PGO, that directly exploits the cycle space. We characterize the topology of the graph as a cycle matrix, and re-parameterize the problem using relative poses, which are further constrained by a cycle basis of the graph. We show that by using a minimum cycle basis, the cycle-based approach has superior convergence properties against its vertex-based counterpart, in terms of convergence speed and convergence to the global minimum. For sparse graphs, our cycle-based approach is also more time efficient than the vertex-based. As an additional contribution of this work we present an effective algorithm to compute the minimum cycle basis. Albeit known in computer science, we believe that this algorithm is not familiar to the robotics community. All the claims are validated by experiments on both standard benchmarks and simulated datasets. To foster the reproduction of the results, we provide a complete open-source C++ implementation (Code: \url{https://bitbucket.org/FangBai/cycleBasedPGO) of our approach.
* 20 pages
Efficient two step optimization for large embedded deformation graph based SLAM
Jun 20, 2019



Abstract:Embedded deformation nodes based formulation has been widely applied in deformable geometry and graphical problems. Though being promising in stereo (or RGBD) sensor based SLAM applications, it remains challenging to keep constant speed in deformation nodes parameter estimation when model grows larger. In practice, the processing time grows rapidly in accordance with the expansion of maps. In this paper, we propose an approach to decouple nodes of deformation graph in large scale dense deformable SLAM and keep the estimation time to be constant. We observe that only partial deformable nodes in the graph are connected to visible points. Based on this fact, sparsity of original Hessian matrix is utilized to split parameter estimation in two independent steps. With this new technique, we achieve faster parameter estimation with amortized computation complexity reduced from O(n^2) to closing O(1). As a result, the computation cost barely increases as the map keeps growing. Based on our strategy, computational bottleneck in large scale embedded deformation graph based applications will be greatly mitigated. The effectiveness is validated by experiments, featuring large scale deformation scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge