The Proxy Step-size Technique for Regularized Optimization on the Sphere Manifold
Paper and Code
Sep 05, 2022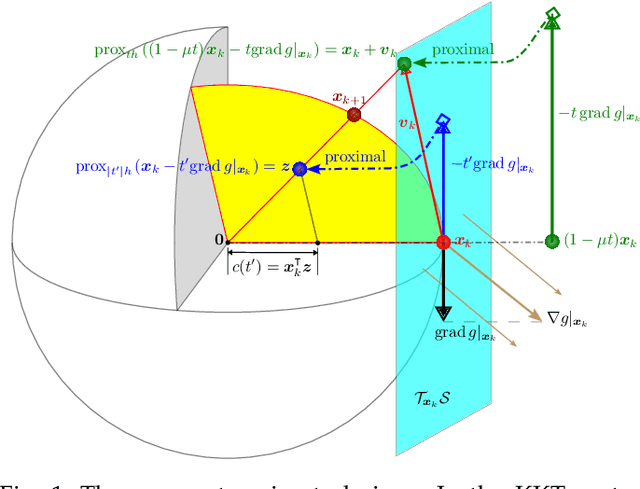
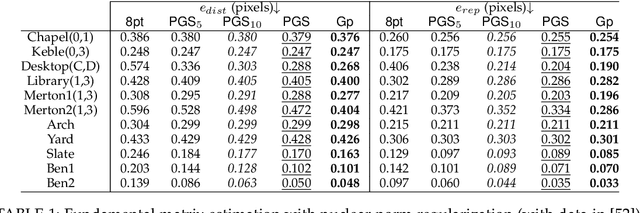
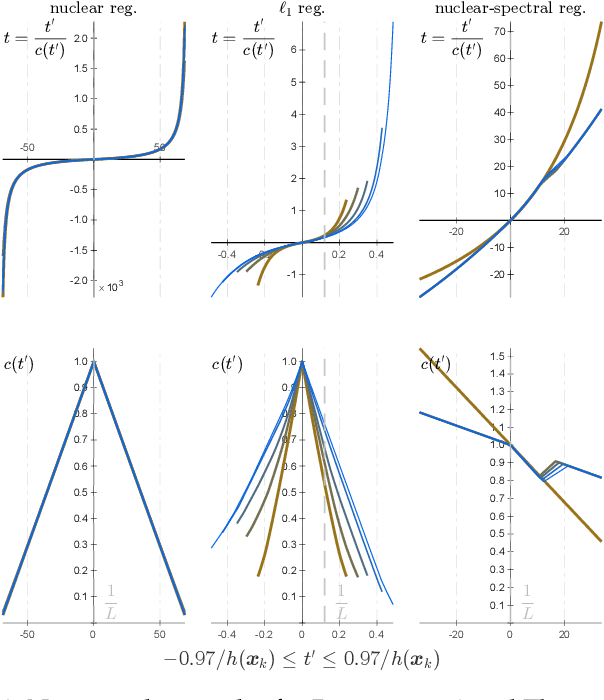
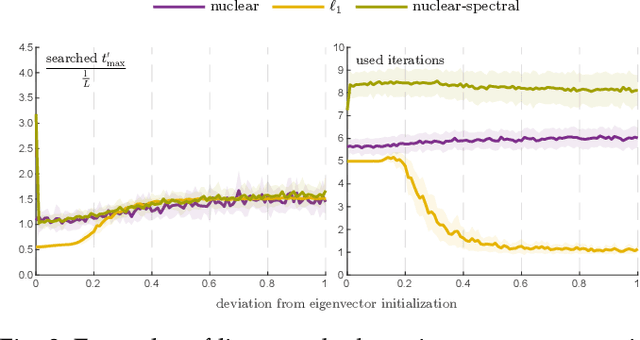
We give an effective solution to the regularized optimization problem $g (\boldsymbol{x}) + h (\boldsymbol{x})$, where $\boldsymbol{x}$ is constrained on the unit sphere $\Vert \boldsymbol{x} \Vert_2 = 1$. Here $g (\cdot)$ is a smooth cost with Lipschitz continuous gradient within the unit ball $\{\boldsymbol{x} : \Vert \boldsymbol{x} \Vert_2 \le 1 \}$ whereas $h (\cdot)$ is typically non-smooth but convex and absolutely homogeneous, \textit{e.g.,}~norm regularizers and their combinations. Our solution is based on the Riemannian proximal gradient, using an idea we call \textit{proxy step-size} -- a scalar variable which we prove is monotone with respect to the actual step-size within an interval. The proxy step-size exists ubiquitously for convex and absolutely homogeneous $h(\cdot)$, and decides the actual step-size and the tangent update in closed-form, thus the complete proximal gradient iteration. Based on these insights, we design a Riemannian proximal gradient method using the proxy step-size. We prove that our method converges to a critical point, guided by a line-search technique based on the $g(\cdot)$ cost only. The proposed method can be implemented in a couple of lines of code. We show its usefulness by applying nuclear norm, $\ell_1$ norm, and nuclear-spectral norm regularization to three classical computer vision problems. The improvements are consistent and backed by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge