Reconstructing the normal and shape at specularities in endoscopy

Specularities are numerous in endoscopic images. They occur as many white small elliptic spots, which are generally ruled out as nuisance in image analysis and computer vision methods. Instead, we propose to use specularities as cues for 3D perception. Specifically, we propose a new method to reconstruct, at each specularity, the observed tissue's normal direction (i.e., its orientation) and shape (i.e., its curvature) from a single image. We show results on simulated and real interventional images.

Normal reconstruction from specularity in the endoscopic setting

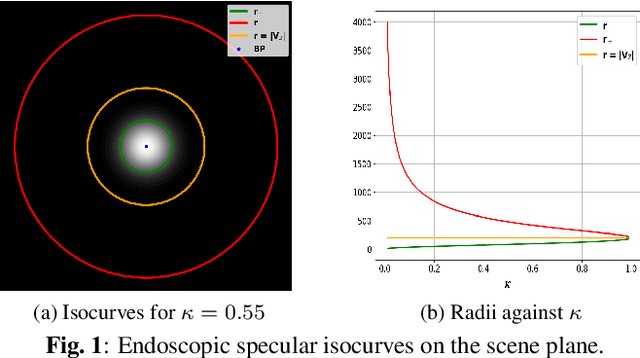
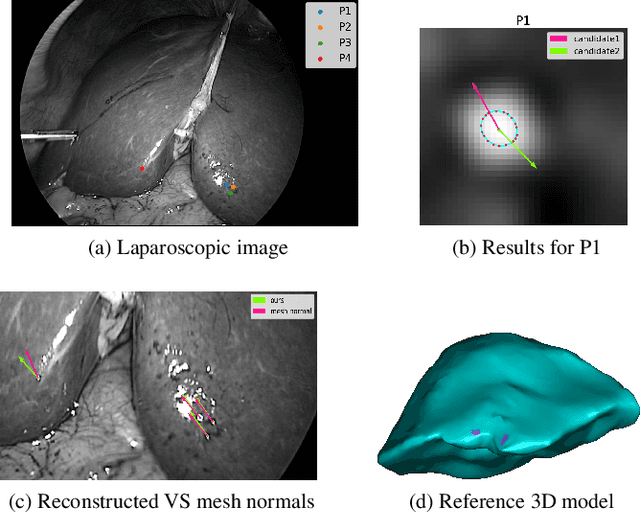
We show that for a plane imaged by an endoscope the specular isophotes are concentric circles on the scene plane, which appear as nested ellipses in the image. We show that these ellipses can be detected and used to estimate the plane's normal direction, forming a normal reconstruction method, which we validate on simulated data. In practice, the anatomical surfaces visible in endoscopic images are locally planar. We use our method to show that the surface normal can thus be reconstructed for each of the numerous specularities typically visible on moist tissues. We show results on laparoscopic and colonoscopic images.

Level set based particle filter driven by optical flow: an application to track the salt boundary from X-ray CT time-series

Image-based computational fluid dynamics have long played an important role in leveraging knowledge and understanding of several physical phenomena. In particular, probabilistic computational methods have opened the way to modelling the complex dynamics of systems in purely random turbulent motion. In the field of structural geology, a better understanding of the deformation and stress state both within the salt and the surrounding rocks is of great interest to characterize all kinds of subsurface long-terms energy-storage systems. The objective of this research is to determine the non-linear deformation of the salt boundary over time using a parallelized, stochastic filtering approach from x-ray computed tomography (CT) image time series depicting the evolution of salt structures triggered by gravity and under differential loading. This work represents a first step towards bringing together physical modeling and advanced stochastic image processing methods where model uncertainty is taken into account.

Characterization of surface motion patterns in highly deformable soft tissue organs from dynamic Magnetic Resonance Imaging

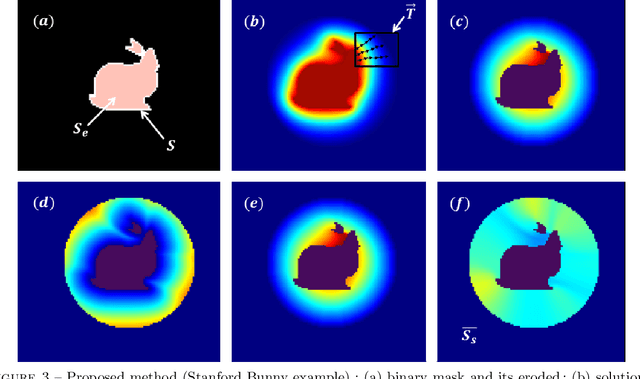
In this work, we present a pipeline for characterization of bladder surface dynamics during deep respiratory movements from dynamic Magnetic Resonance Imaging (MRI). Dynamic MRI may capture temporal anatomical changes in soft tissue organs with high-contrast but the obtained sequences usually suffer from limited volume coverage which makes the high resolution reconstruction of organ shape trajectories a major challenge in temporal studies. For a compact shape representation, the reconstructed temporal data with full volume coverage are first used to establish a subject-specific dynamical 4D mesh sequences using the large deformation diffeomorphic metric mapping (LDDMM) framework. Then, we performed a statistical characterization of organ shape changes from mechanical parameters such as mesh elongations and distortions. Since shape space is curved, we have also used the intrinsic curvature changes as metric to quantify surface evolution. However, the numerical computation of curvature is strongly dependant on the surface parameterization (i.e. the mesh resolution). To cope with this dependency, we propose a non-parametric level set method to evaluate spatio-temporal surface evolution. Independent of parameterization and minimizing the length of the geodesic curves, it shrinks smoothly the surface curves towards a sphere by minimizing a Dirichlet energy. An Eulerian PDE approach is used for evaluation of surface dynamics from the curve-shortening flow. Results demonstrate the numerical stability of the derived descriptor throughout smooth continuous-time organ trajectories. Intercorrelations between individuals' motion patterns from different geometric features are computed using the Laplace-Beltrami Operator (LBO) eigenfunctions for spherical mapping.

A new geodesic-based feature for characterization of 3D shapes: application to soft tissue organ temporal deformations

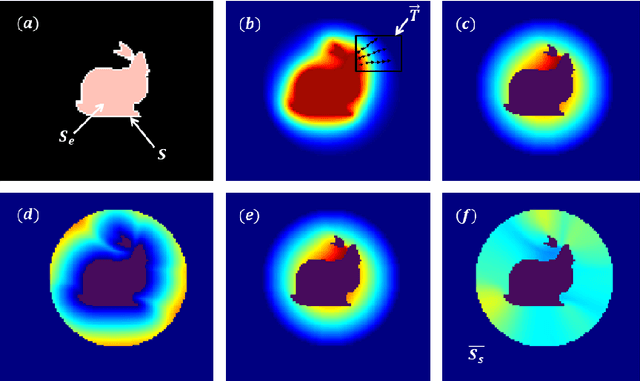
In this paper, we propose a method for characterizing 3D shapes from point clouds and we show a direct application on a study of organ temporal deformations. As an example, we characterize the behavior of a bladder during a forced respiratory motion with a reduced number of 3D surface points: first, a set of equidistant points representing the vertices of quadrilateral mesh for the surface in the first time frame are tracked throughout a long dynamic MRI sequence using a Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework. Second, a novel geometric feature which is invariant to scaling and rotation is proposed for characterizing the temporal organ deformations by employing an Eulerian Partial Differential Equations (PDEs) methodology. We demonstrate the robustness of our feature on both synthetic 3D shapes and realistic dynamic MRI data portraying the bladder deformation during forced respiratory motions. Promising results are obtained, showing that the proposed feature may be useful for several computer vision applications such as medical imaging, aerodynamics and robotics.