Deep learning complete intersection Calabi-Yau manifolds

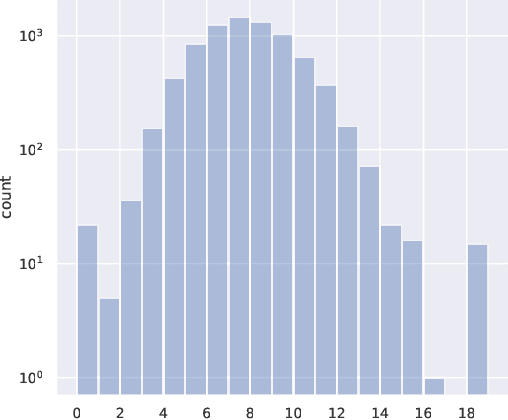
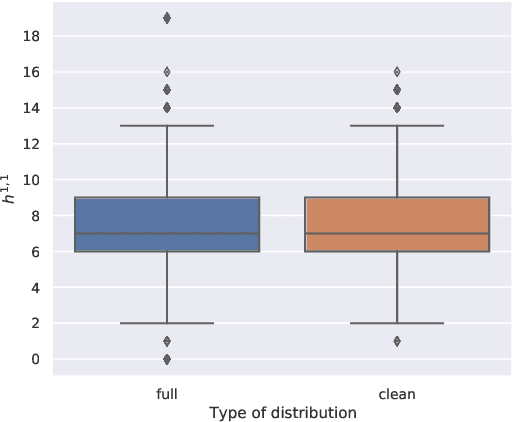
We review advancements in deep learning techniques for complete intersection Calabi-Yau (CICY) 3- and 4-folds, with the aim of understanding better how to handle algebraic topological data with machine learning. We first discuss methodological aspects and data analysis, before describing neural networks architectures. Then, we describe the state-of-the art accuracy in predicting Hodge numbers. We include new results on extrapolating predictions from low to high Hodge numbers, and conversely.

Renormalization in the neural network-quantum field theory correspondence

A statistical ensemble of neural networks can be described in terms of a quantum field theory (NN-QFT correspondence). The infinite-width limit is mapped to a free field theory, while finite N corrections are mapped to interactions. After reviewing the correspondence, we will describe how to implement renormalization in this context and discuss preliminary numerical results for translation-invariant kernels. A major outcome is that changing the standard deviation of the neural network weight distribution corresponds to a renormalization flow in the space of networks.

Characterizing 4-string contact interaction using machine learning

The geometry of 4-string contact interaction of closed string field theory is characterized using machine learning. We obtain Strebel quadratic differentials on 4-punctured spheres as a neural network by performing unsupervised learning with a custom-built loss function. This allows us to solve for local coordinates and compute their associated mapping radii numerically. We also train a neural network distinguishing vertex from Feynman region. As a check, 4-tachyon contact term in the tachyon potential is computed and a good agreement with the results in the literature is observed. We argue that our algorithm is manifestly independent of number of punctures and scaling it to characterize the geometry of $n$-string contact interaction is feasible.

Deep multi-task mining Calabi-Yau four-folds

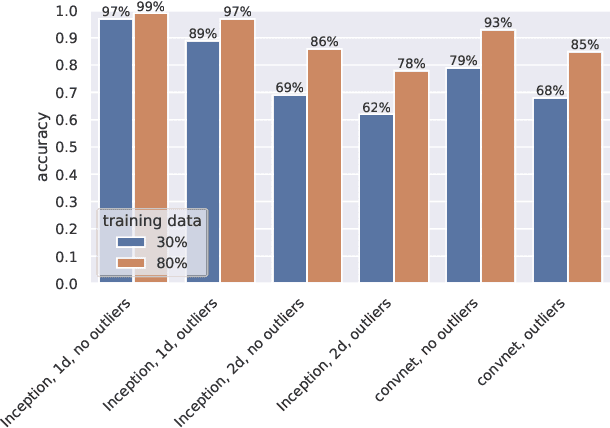
We continue earlier efforts in computing the dimensions of tangent space cohomologies of Calabi-Yau manifolds using deep learning. In this paper, we consider the dataset of all Calabi-Yau four-folds constructed as complete intersections in products of projective spaces. Employing neural networks inspired by state-of-the-art computer vision architectures, we improve earlier benchmarks and demonstrate that all four non-trivial Hodge numbers can be learned at the same time using a multi-task architecture. With 30% (80%) training ratio, we reach an accuracy of 100% for $h^{(1,1)}$ and 97% for $h^{(2,1)}$ (100% for both), 81% (96%) for $h^{(3,1)}$, and 49% (83%) for $h^{(2,2)}$. Assuming that the Euler number is known, as it is easy to compute, and taking into account the linear constraint arising from index computations, we get 100% total accuracy.

Nonperturbative renormalization for the neural network-QFT correspondence

In a recent work arXiv:2008.08601, Halverson, Maiti and Stoner proposed a description of neural networks in terms of a Wilsonian effective field theory. The infinite-width limit is mapped to a free field theory, while finite $N$ corrections are taken into account by interactions (non-Gaussian terms in the action). In this paper, we study two related aspects of this correspondence. First, we comment on the concepts of locality and power-counting in this context. Indeed, these usual space-time notions may not hold for neural networks (since inputs can be arbitrary), however, the renormalization group provides natural notions of locality and scaling. Moreover, we comment on several subtleties, for example, that data components may not have a permutation symmetry: in that case, we argue that random tensor field theories could provide a natural generalization. Second, we improve the perturbative Wilsonian renormalization from arXiv:2008.08601 by providing an analysis in terms of the nonperturbative renormalization group using the Wetterich-Morris equation. An important difference with usual nonperturbative RG analysis is that only the effective (IR) 2-point function is known, which requires setting the problem with care. Our aim is to provide a useful formalism to investigate neural networks behavior beyond the large-width limit (i.e.~far from Gaussian limit) in a nonperturbative fashion. A major result of our analysis is that changing the standard deviation of the neural network weight distribution can be interpreted as a renormalization flow in the space of networks. We focus on translations invariant kernels and provide preliminary numerical results.

Machine learning for complete intersection Calabi-Yau manifolds: a methodological study

We revisit the question of predicting both Hodge numbers $h^{1,1}$ and $h^{2,1}$ of complete intersection Calabi-Yau (CICY) 3-folds using machine learning (ML), considering both the old and new datasets built respectively by Candelas-Dale-Lutken-Schimmrigk / Green-H\"ubsch-Lutken and by Anderson-Gao-Gray-Lee. In real world applications, implementing a ML system rarely reduces to feed the brute data to the algorithm. Instead, the typical workflow starts with an exploratory data analysis (EDA) which aims at understanding better the input data and finding an optimal representation. It is followed by the design of a validation procedure and a baseline model. Finally, several ML models are compared and combined, often involving neural networks with a topology more complicated than the sequential models typically used in physics. By following this procedure, we improve the accuracy of ML computations for Hodge numbers with respect to the existing literature. First, we obtain 97% (resp. 99%) accuracy for $h^{1,1}$ using a neural network inspired by the Inception model for the old dataset, using only 30% (resp. 70%) of the data for training. For the new one, a simple linear regression leads to almost 100% accuracy with 30% of the data for training. The computation of $h^{2,1}$ is less successful as we manage to reach only 50% accuracy for both datasets, but this is still better than the 16% obtained with a simple neural network (SVM with Gaussian kernel and feature engineering and sequential convolutional network reach at best 36%). This serves as a proof of concept that neural networks can be valuable to study the properties of geometries appearing in string theory.

Inception Neural Network for Complete Intersection Calabi-Yau 3-folds

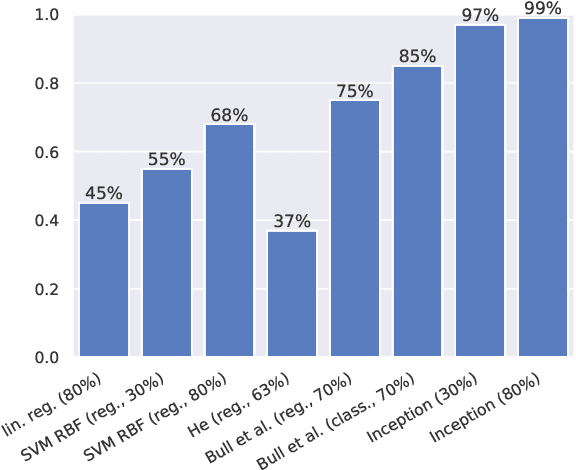
We introduce a neural network inspired by Google's Inception model to compute the Hodge number $h^{1,1}$ of complete intersection Calabi-Yau (CICY) 3-folds. This architecture improves largely the accuracy of the predictions over existing results, giving already 97% of accuracy with just 30% of the data for training. Moreover, accuracy climbs to 99% when using 80% of the data for training. This proves that neural networks are a valuable resource to study geometric aspects in both pure mathematics and string theory.

Topological defects and confinement with machine learning: the case of monopoles in compact electrodynamics

We investigate the advantages of machine learning techniques to recognize the dynamics of topological objects in quantum field theories. We consider the compact U(1) gauge theory in three spacetime dimensions as the simplest example of a theory that exhibits confinement and mass gap phenomena generated by monopoles. We train a neural network with a generated set of monopole configurations to distinguish between confinement and deconfinement phases, from which it is possible to determine the deconfinement transition point and to predict several observables. The model uses a supervised learning approach and treats the monopole configurations as three-dimensional images (holograms). We show that the model can determine the transition temperature with accuracy, which depends on the criteria implemented in the algorithm. More importantly, we train the neural network with configurations from a single lattice size before making predictions for configurations from other lattice sizes, from which a reliable estimation of the critical temperatures are obtained.

Casimir effect with machine learning

Vacuum fluctuations of quantum fields between physical objects depend on the shapes, positions, and internal composition of the latter. For objects of arbitrary shapes, even made from idealized materials, the calculation of the associated zero-point (Casimir) energy is an analytically intractable challenge. We propose a new numerical approach to this problem based on machine-learning techniques and illustrate the effectiveness of the method in a (2+1) dimensional scalar field theory. The Casimir energy is first calculated numerically using a Monte-Carlo algorithm for a set of the Dirichlet boundaries of various shapes. Then, a neural network is trained to compute this energy given the Dirichlet domain, treating the latter as black-and-white pixelated images. We show that after the learning phase, the neural network is able to quickly predict the Casimir energy for new boundaries of general shapes with reasonable accuracy.

GANs for generating EFT models

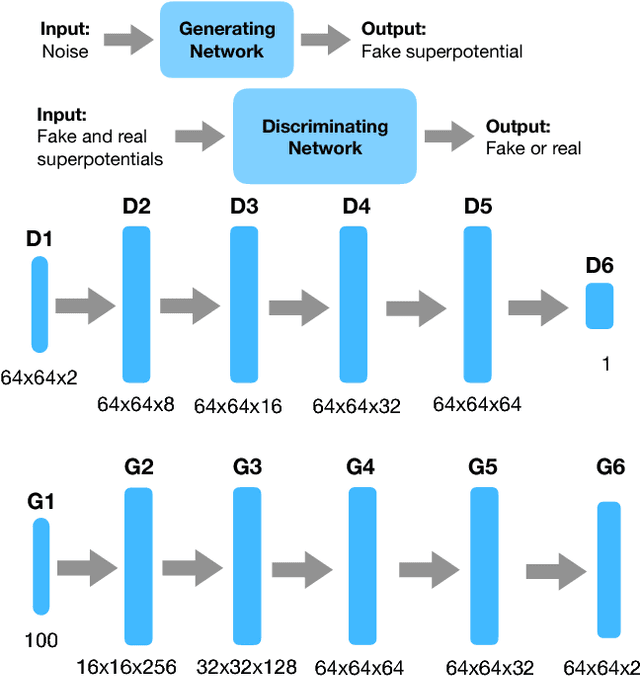
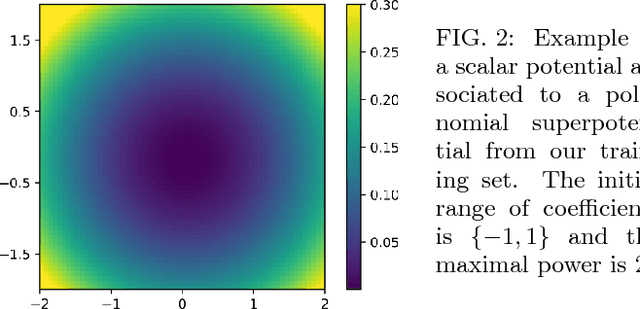
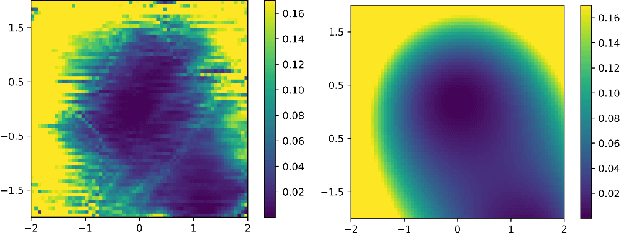
We initiate a way of generating models by the computer, satisfying both experimental and theoretical constraints. In particular, we present a framework which allows the generation of effective field theories. We use Generative Adversarial Networks to generate these models and we generate examples which go beyond the examples known to the machine. As a starting point, we apply this idea to the generation of supersymmetric field theories. In this case, the machine knows consistent examples of supersymmetric field theories with a single field and generates new examples of such theories. In the generated potentials we find distinct properties, here the number of minima in the scalar potential, with values not found in the training data. We comment on potential further applications of this framework.