PICZL: Image-based Photometric Redshifts for AGN

Computing photo-z for AGN is challenging, primarily due to the interplay of relative emissions associated with the SMBH and its host galaxy. SED fitting methods, effective in pencil-beam surveys, face limitations in all-sky surveys with fewer bands available, lacking the ability to capture the AGN contribution to the SED accurately. This limitation affects the many 10s of millions of AGN clearly singled out and identified by SRG/eROSITA. Our goal is to significantly enhance photometric redshift performance for AGN in all-sky surveys while avoiding the need to merge multiple data sets. Instead, we employ readily available data products from the 10th Data Release of the Imaging Legacy Survey for DESI, covering > 20,000 deg$^{2}$ with deep images and catalog-based photometry in the grizW1-W4 bands. We introduce PICZL, a machine-learning algorithm leveraging an ensemble of CNNs. Utilizing a cross-channel approach, the algorithm integrates distinct SED features from images with those obtained from catalog-level data. Full probability distributions are achieved via the integration of Gaussian mixture models. On a validation sample of 8098 AGN, PICZL achieves a variance $\sigma_{\textrm{NMAD}}$ of 4.5% with an outlier fraction $\eta$ of 5.6%, outperforming previous attempts to compute accurate photo-z for AGN using ML. We highlight that the model's performance depends on many variables, predominantly the depth of the data. A thorough evaluation of these dependencies is presented in the paper. Our streamlined methodology maintains consistent performance across the entire survey area when accounting for differing data quality. The same approach can be adopted for future deep photometric surveys such as LSST and Euclid, showcasing its potential for wide-scale realisation. With this paper, we release updated photo-z (including errors) for the XMM-SERVS W-CDF-S, ELAIS-S1 and LSS fields.

Collective variables of neural networks: empirical time evolution and scaling laws

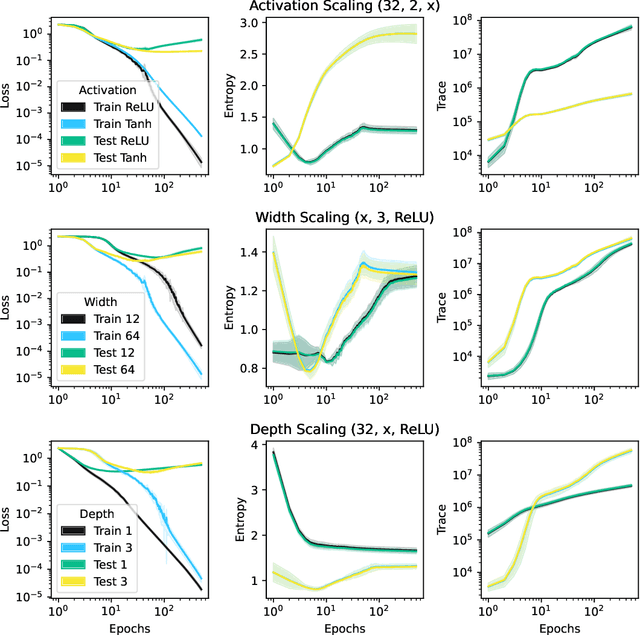
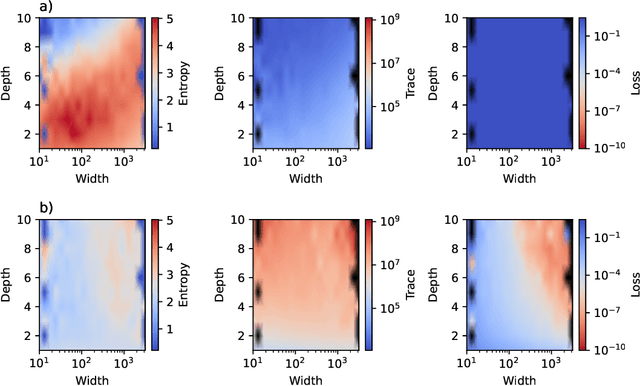
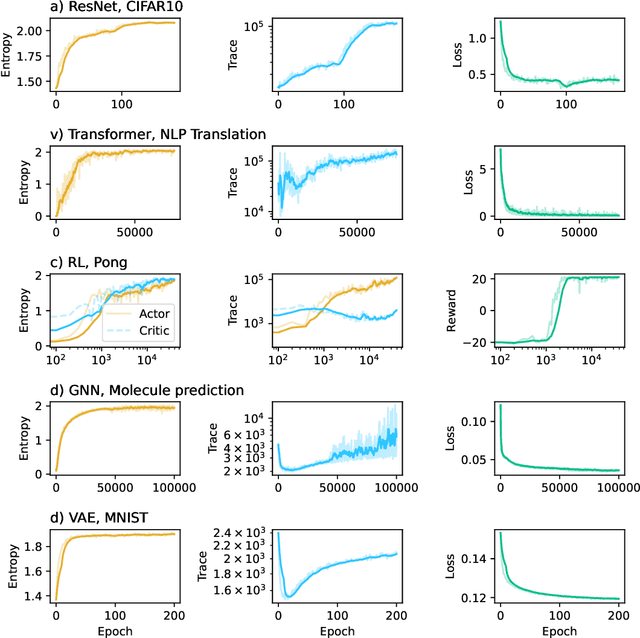
This work presents a novel means for understanding learning dynamics and scaling relations in neural networks. We show that certain measures on the spectrum of the empirical neural tangent kernel, specifically entropy and trace, yield insight into the representations learned by a neural network and how these can be improved through architecture scaling. These results are demonstrated first on test cases before being shown on more complex networks, including transformers, auto-encoders, graph neural networks, and reinforcement learning studies. In testing on a wide range of architectures, we highlight the universal nature of training dynamics and further discuss how it can be used to understand the mechanisms behind learning in neural networks. We identify two such dominant mechanisms present throughout machine learning training. The first, information compression, is seen through a reduction in the entropy of the NTK spectrum during training, and occurs predominantly in small neural networks. The second, coined structure formation, is seen through an increasing entropy and thus, the creation of structure in the neural network representations beyond the prior established by the network at initialization. Due to the ubiquity of the latter in deep neural network architectures and its flexibility in the creation of feature-rich representations, we argue that this form of evolution of the network's entropy be considered the onset of a deep learning regime.

Towards a Phenomenological Understanding of Neural Networks: Data

A theory of neural networks (NNs) built upon collective variables would provide scientists with the tools to better understand the learning process at every stage. In this work, we introduce two such variables, the entropy and the trace of the empirical neural tangent kernel (NTK) built on the training data passed to the model. We empirically analyze the NN performance in the context of these variables and find that there exists correlation between the starting entropy, the trace of the NTK, and the generalization of the model computed after training is complete. This framework is then applied to the problem of optimal data selection for the training of NNs. To this end, random network distillation (RND) is used as a means of selecting training data which is then compared with random selection of data. It is shown that not only does RND select data-sets capable of outperforming random selection, but that the collective variables associated with the RND data-sets are larger than those of the randomly selected sets. The results of this investigation provide a stable ground from which the selection of data for NN training can be driven by this phenomenological framework.

A duality connecting neural network and cosmological dynamics

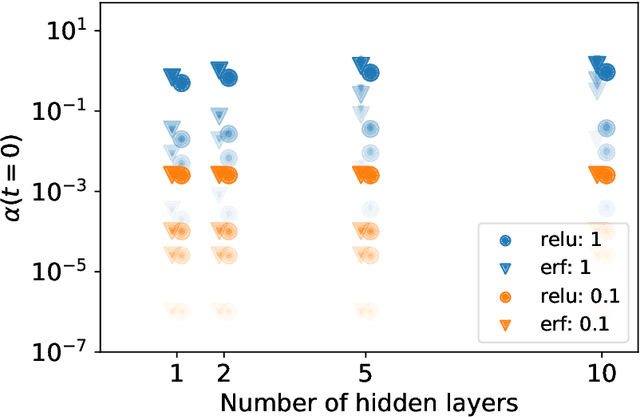
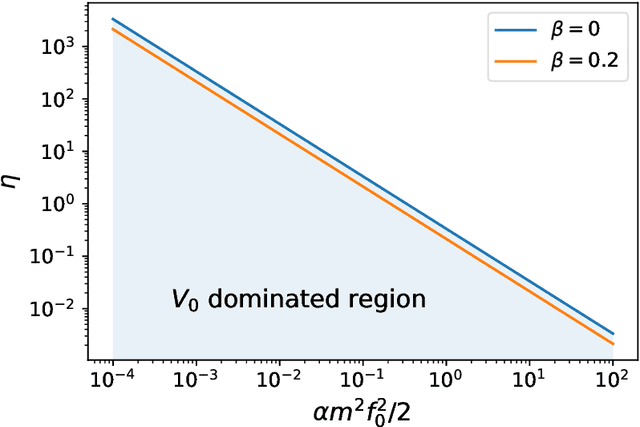
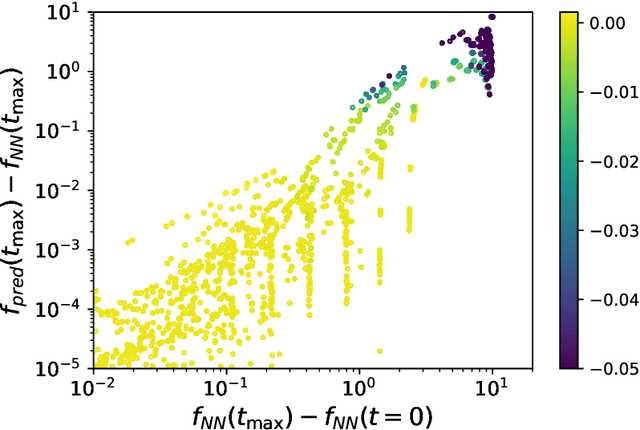
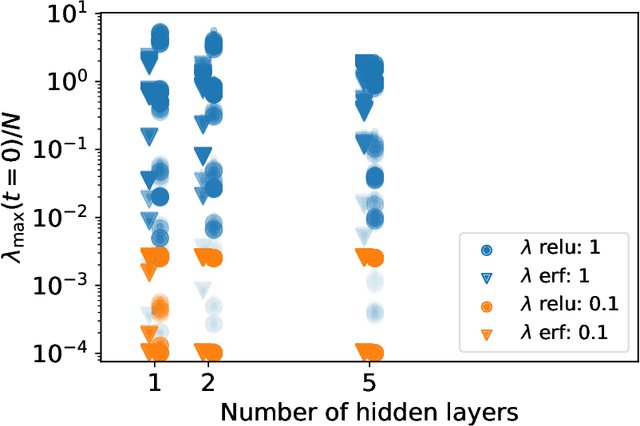
We demonstrate that the dynamics of neural networks trained with gradient descent and the dynamics of scalar fields in a flat, vacuum energy dominated Universe are structurally profoundly related. This duality provides the framework for synergies between these systems, to understand and explain neural network dynamics and new ways of simulating and describing early Universe models. Working in the continuous-time limit of neural networks, we analytically match the dynamics of the mean background and the dynamics of small perturbations around the mean field, highlighting potential differences in separate limits. We perform empirical tests of this analytic description and quantitatively show the dependence of the effective field theory parameters on hyperparameters of the neural network. As a result of this duality, the cosmological constant is matched inversely to the learning rate in the gradient descent update.

Improving Simulations with Symmetry Control Neural Networks

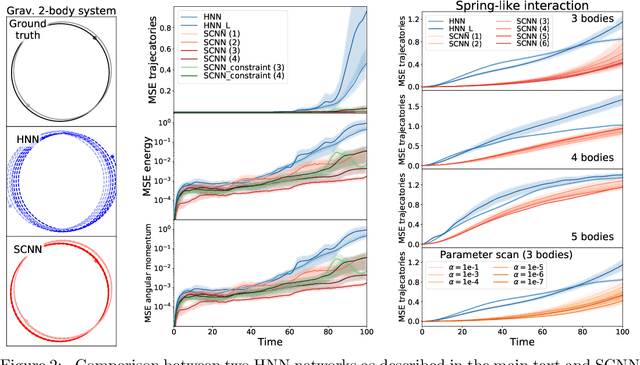
The dynamics of physical systems is often constrained to lower dimensional sub-spaces due to the presence of conserved quantities. Here we propose a method to learn and exploit such symmetry constraints building upon Hamiltonian Neural Networks. By enforcing cyclic coordinates with appropriate loss functions, we find that we can achieve improved accuracy on simple classical dynamics tasks. By fitting analytic formulae to the latent variables in our network we recover that our networks are utilizing conserved quantities such as (angular) momentum.

Detecting Symmetries with Neural Networks

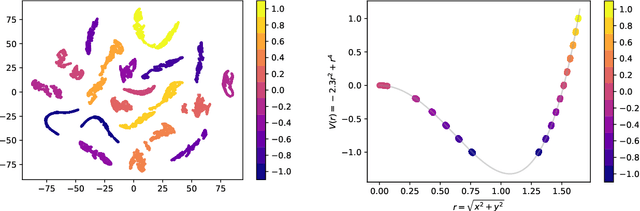
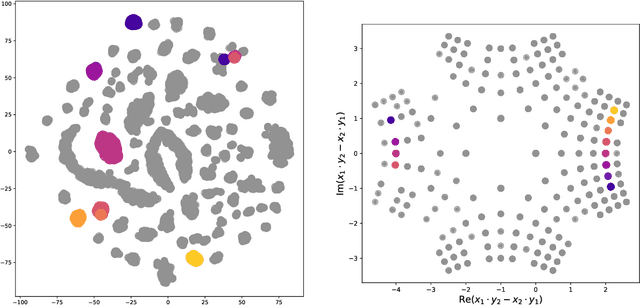
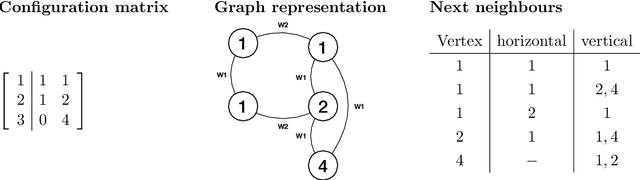
Identifying symmetries in data sets is generally difficult, but knowledge about them is crucial for efficient data handling. Here we present a method how neural networks can be used to identify symmetries. We make extensive use of the structure in the embedding layer of the neural network which allows us to identify whether a symmetry is present and to identify orbits of the symmetry in the input. To determine which continuous or discrete symmetry group is present we analyse the invariant orbits in the input. We present examples based on rotation groups $SO(n)$ and the unitary group $SU(2).$ Further we find that this method is useful for the classification of complete intersection Calabi-Yau manifolds where it is crucial to identify discrete symmetries on the input space. For this example we present a novel data representation in terms of graphs.

Connecting Dualities and Machine Learning

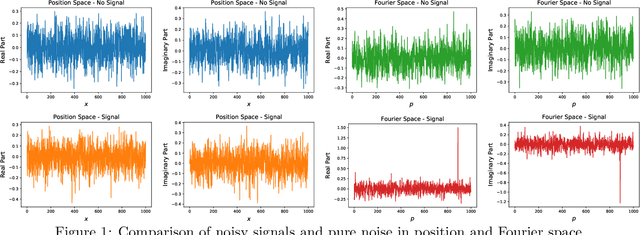
Dualities are widely used in quantum field theories and string theory to obtain correlation functions at high accuracy. Here we present examples where dual data representations are useful in supervised classification, linking machine learning and typical tasks in theoretical physics. We then discuss how such beneficial representations can be enforced in the latent dimension of neural networks. We find that additional contributions to the loss based on feature separation, feature matching with respect to desired representations, and a good performance on a `simple' correlation function can lead to known and unknown dual representations. This is the first proof of concept that computers can find dualities. We discuss how our examples, based on discrete Fourier transformation and Ising models, connect to other dualities in theoretical physics, for instance Seiberg duality.

GANs for generating EFT models

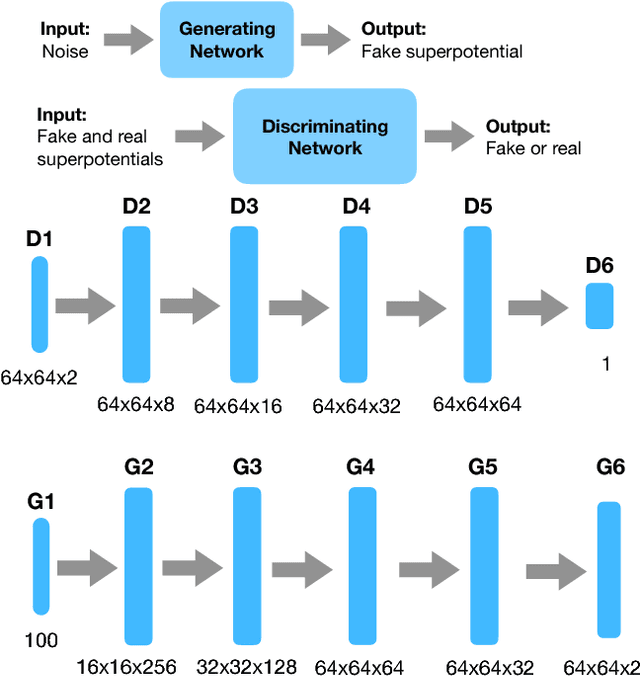
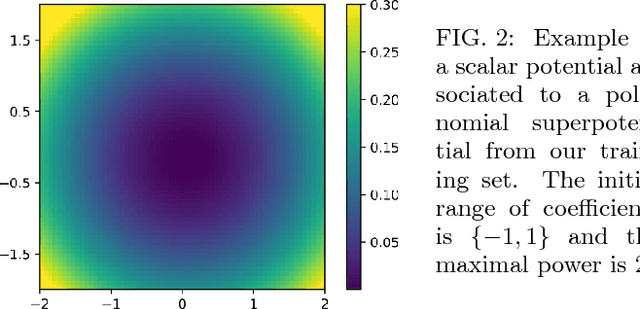
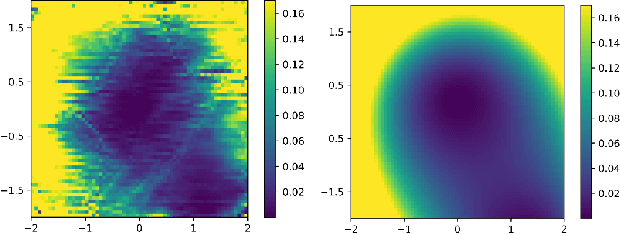
We initiate a way of generating models by the computer, satisfying both experimental and theoretical constraints. In particular, we present a framework which allows the generation of effective field theories. We use Generative Adversarial Networks to generate these models and we generate examples which go beyond the examples known to the machine. As a starting point, we apply this idea to the generation of supersymmetric field theories. In this case, the machine knows consistent examples of supersymmetric field theories with a single field and generates new examples of such theories. In the generated potentials we find distinct properties, here the number of minima in the scalar potential, with values not found in the training data. We comment on potential further applications of this framework.