Improving Simulations with Symmetry Control Neural Networks
Paper and Code
Apr 29, 2021

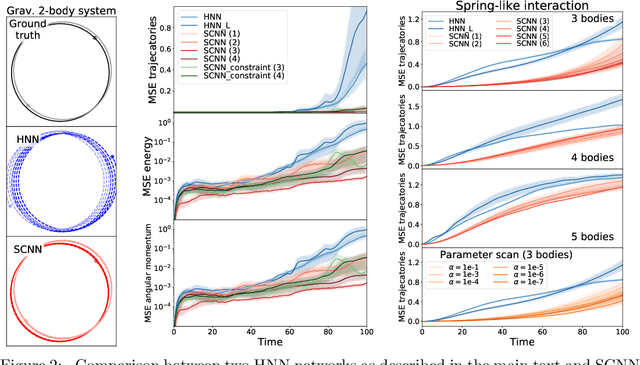
The dynamics of physical systems is often constrained to lower dimensional sub-spaces due to the presence of conserved quantities. Here we propose a method to learn and exploit such symmetry constraints building upon Hamiltonian Neural Networks. By enforcing cyclic coordinates with appropriate loss functions, we find that we can achieve improved accuracy on simple classical dynamics tasks. By fitting analytic formulae to the latent variables in our network we recover that our networks are utilizing conserved quantities such as (angular) momentum.
* 7 pages, 2 figures, accepted as workshop paper at ICLR 2021 SimDL
Workshop
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge