Improving Simulations with Symmetry Control Neural Networks

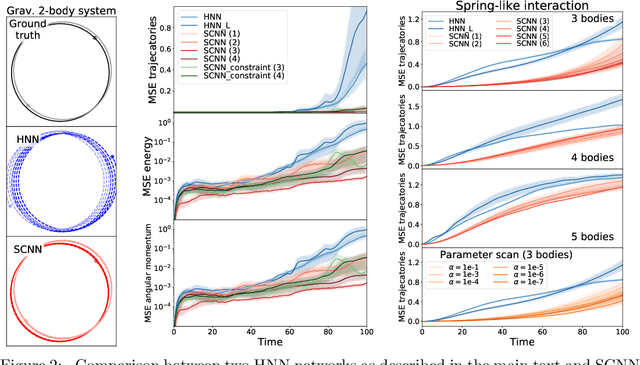
The dynamics of physical systems is often constrained to lower dimensional sub-spaces due to the presence of conserved quantities. Here we propose a method to learn and exploit such symmetry constraints building upon Hamiltonian Neural Networks. By enforcing cyclic coordinates with appropriate loss functions, we find that we can achieve improved accuracy on simple classical dynamics tasks. By fitting analytic formulae to the latent variables in our network we recover that our networks are utilizing conserved quantities such as (angular) momentum.

Detecting Symmetries with Neural Networks

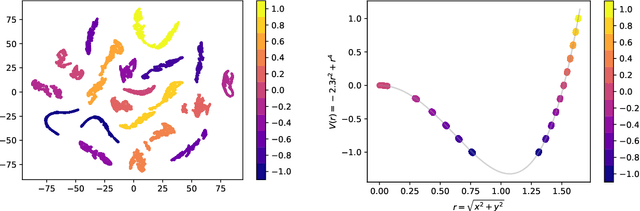
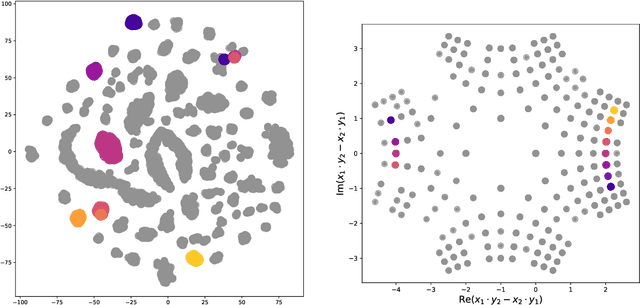
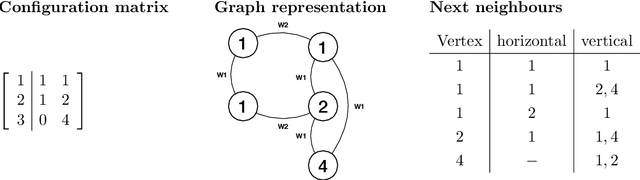
Identifying symmetries in data sets is generally difficult, but knowledge about them is crucial for efficient data handling. Here we present a method how neural networks can be used to identify symmetries. We make extensive use of the structure in the embedding layer of the neural network which allows us to identify whether a symmetry is present and to identify orbits of the symmetry in the input. To determine which continuous or discrete symmetry group is present we analyse the invariant orbits in the input. We present examples based on rotation groups $SO(n)$ and the unitary group $SU(2).$ Further we find that this method is useful for the classification of complete intersection Calabi-Yau manifolds where it is crucial to identify discrete symmetries on the input space. For this example we present a novel data representation in terms of graphs.