Communicating Likelihoods with Normalising Flows

We present a machine-learning-based workflow to model an unbinned likelihood from its samples. A key advancement over existing approaches is the validation of the learned likelihood using rigorous statistical tests of the joint distribution, such as the Kolmogorov-Smirnov test of the joint distribution. Our method enables the reliable communication of experimental and phenomenological likelihoods for subsequent analyses. We demonstrate its effectiveness through three case studies in high-energy physics. To support broader adoption, we provide an open-source reference implementation, nabu.

Optimal Equivariant Architectures from the Symmetries of Matrix-Element Likelihoods

The Matrix-Element Method (MEM) has long been a cornerstone of data analysis in high-energy physics. It leverages theoretical knowledge of parton-level processes and symmetries to evaluate the likelihood of observed events. In parallel, the advent of geometric deep learning has enabled neural network architectures that incorporate known symmetries directly into their design, leading to more efficient learning. This paper presents a novel approach that combines MEM-inspired symmetry considerations with equivariant neural network design for particle physics analysis. Even though Lorentz invariance and permutation invariance overall reconstructed objects are the largest and most natural symmetry in the input domain, we find that they are sub-optimal in most practical search scenarios. We propose a longitudinal boost-equivariant message-passing neural network architecture that preserves relevant discrete symmetries. We present numerical studies demonstrating MEM-inspired architectures achieve new state-of-the-art performance in distinguishing di-Higgs decays to four bottom quarks from the QCD background, with enhanced sample and parameter efficiencies. This synergy between MEM and equivariant deep learning opens new directions for physics-informed architecture design, promising more powerful tools for probing physics beyond the Standard Model.

Collective variables of neural networks: empirical time evolution and scaling laws

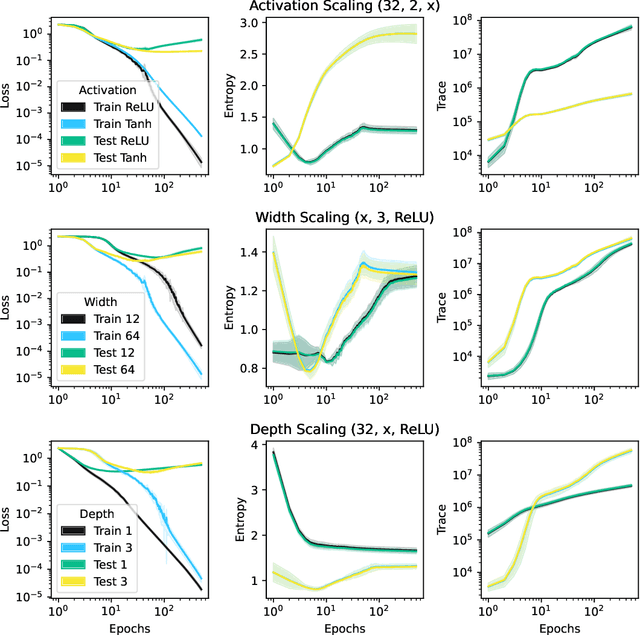
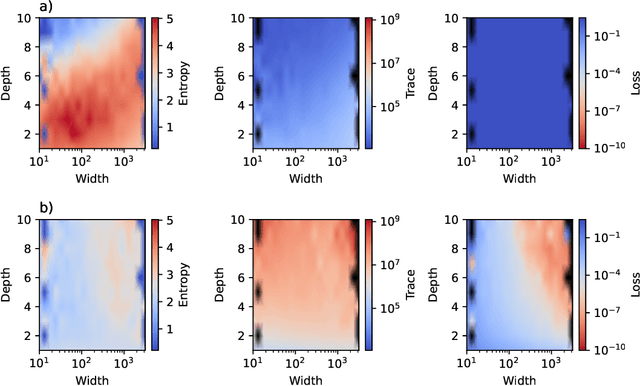
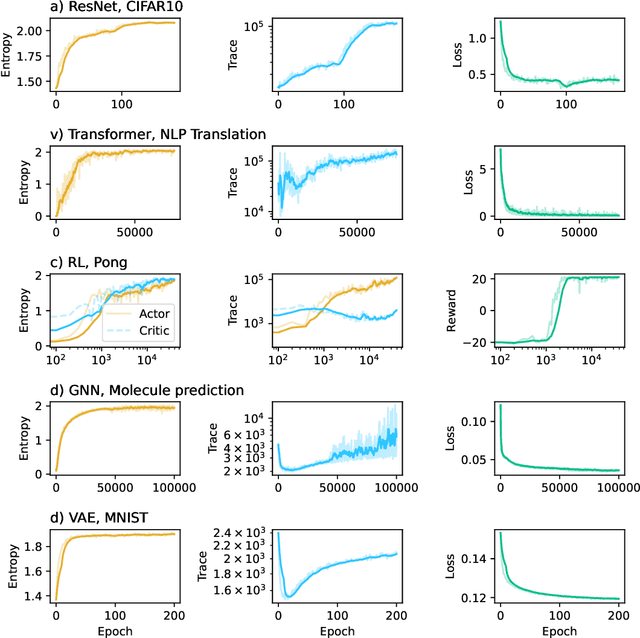
This work presents a novel means for understanding learning dynamics and scaling relations in neural networks. We show that certain measures on the spectrum of the empirical neural tangent kernel, specifically entropy and trace, yield insight into the representations learned by a neural network and how these can be improved through architecture scaling. These results are demonstrated first on test cases before being shown on more complex networks, including transformers, auto-encoders, graph neural networks, and reinforcement learning studies. In testing on a wide range of architectures, we highlight the universal nature of training dynamics and further discuss how it can be used to understand the mechanisms behind learning in neural networks. We identify two such dominant mechanisms present throughout machine learning training. The first, information compression, is seen through a reduction in the entropy of the NTK spectrum during training, and occurs predominantly in small neural networks. The second, coined structure formation, is seen through an increasing entropy and thus, the creation of structure in the neural network representations beyond the prior established by the network at initialization. Due to the ubiquity of the latter in deep neural network architectures and its flexibility in the creation of feature-rich representations, we argue that this form of evolution of the network's entropy be considered the onset of a deep learning regime.

The role of data embedding in quantum autoencoders for improved anomaly detection

The performance of Quantum Autoencoders (QAEs) in anomaly detection tasks is critically dependent on the choice of data embedding and ansatz design. This study explores the effects of three data embedding techniques, data re-uploading, parallel embedding, and alternate embedding, on the representability and effectiveness of QAEs in detecting anomalies. Our findings reveal that even with relatively simple variational circuits, enhanced data embedding strategies can substantially improve anomaly detection accuracy and the representability of underlying data across different datasets. Starting with toy examples featuring low-dimensional data, we visually demonstrate the effect of different embedding techniques on the representability of the model. We then extend our analysis to complex, higher-dimensional datasets, highlighting the significant impact of embedding methods on QAE performance.

Optimal Symmetries in Binary Classification

We explore the role of group symmetries in binary classification tasks, presenting a novel framework that leverages the principles of Neyman-Pearson optimality. Contrary to the common intuition that larger symmetry groups lead to improved classification performance, our findings show that selecting the appropriate group symmetries is crucial for optimising generalisation and sample efficiency. We develop a theoretical foundation for designing group equivariant neural networks that align the choice of symmetries with the underlying probability distributions of the data. Our approach provides a unified methodology for improving classification accuracy across a broad range of applications by carefully tailoring the symmetry group to the specific characteristics of the problem. Theoretical analysis and experimental results demonstrate that optimal classification performance is not always associated with the largest equivariant groups possible in the domain, even when the likelihood ratio is invariant under one of its proper subgroups, but rather with those subgroups themselves. This work offers insights and practical guidelines for constructing more effective group equivariant architectures in diverse machine-learning contexts.

Training Neural Networks with Universal Adiabatic Quantum Computing

The training of neural networks (NNs) is a computationally intensive task requiring significant time and resources. This paper presents a novel approach to NN training using Adiabatic Quantum Computing (AQC), a paradigm that leverages the principles of adiabatic evolution to solve optimisation problems. We propose a universal AQC method that can be implemented on gate quantum computers, allowing for a broad range of Hamiltonians and thus enabling the training of expressive neural networks. We apply this approach to various neural networks with continuous, discrete, and binary weights. Our results indicate that AQC can very efficiently find the global minimum of the loss function, offering a promising alternative to classical training methods.

Generative Invertible Quantum Neural Networks

Invertible Neural Networks (INN) have become established tools for the simulation and generation of highly complex data. We propose a quantum-gate algorithm for a Quantum Invertible Neural Network (QINN) and apply it to the LHC data of jet-associated production of a Z-boson that decays into leptons, a standard candle process for particle collider precision measurements. We compare the QINN's performance for different loss functions and training scenarios. For this task, we find that a hybrid QINN matches the performance of a significantly larger purely classical INN in learning and generating complex data.

Quantum-probabilistic Hamiltonian learning for generative modelling & anomaly detection

The Hamiltonian of an isolated quantum mechanical system determines its dynamics and physical behaviour. This study investigates the possibility of learning and utilising a system's Hamiltonian and its variational thermal state estimation for data analysis techniques. For this purpose, we employ the method of Quantum Hamiltonian-Based Models for the generative modelling of simulated Large Hadron Collider data and demonstrate the representability of such data as a mixed state. In a further step, we use the learned Hamiltonian for anomaly detection, showing that different sample types can form distinct dynamical behaviours once treated as a quantum many-body system. We exploit these characteristics to quantify the difference between sample types. Our findings show that the methodologies designed for field theory computations can be utilised in machine learning applications to employ theoretical approaches in data analysis techniques.

A Genetic Quantum Annealing Algorithm

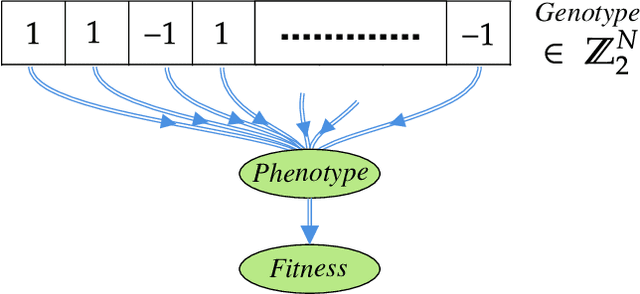
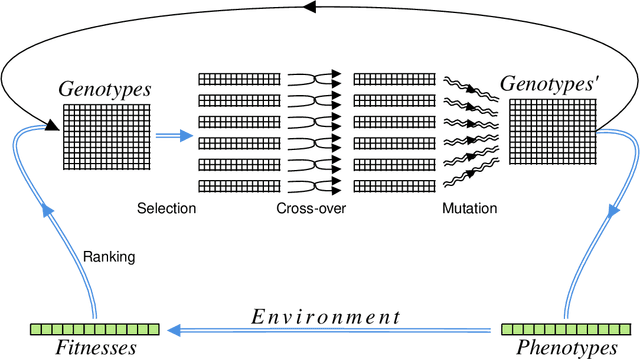
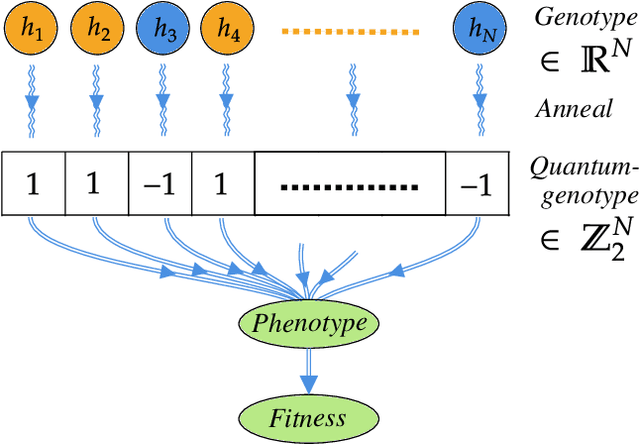
A genetic algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Natural Selection. We present an algorithm which enhances the classical GA with input from quantum annealers. As in a classical GA, the algorithm works by breeding a population of possible solutions based on their fitness. However, the population of individuals is defined by the continuous couplings on the quantum annealer, which then give rise via quantum annealing to the set of corresponding phenotypes that represent attempted solutions. This introduces a form of directed mutation into the algorithm that can enhance its performance in various ways. Two crucial enhancements come from the continuous couplings having strengths that are inherited from the fitness of the parents (so-called nepotism) and from the annealer couplings allowing the entire population to be influenced by the fittest individuals (so-called quantum-polyandry). We find our algorithm to be significantly more powerful on several simple problems than a classical GA.

Identifying (anti-)skyrmions while they form

We use a Convolutional Neural Network (CNN) to identify the relevant features in the thermodynamical phases of a simulated three-dimensional spin-lattice system with ferromagnetic and Dzyaloshinskii-Moriya (DM) interactions. Such features include (anti-)skyrmions, merons, and helical and ferromagnetic states. We use a multi-label classification framework, which is flexible enough to accommodate states that mix different features and phases. We then train the CNN to predict the features of the final state from snapshots of intermediate states of the simulation. The trained model allows identifying the different phases reliably and early in the formation process. Thus, the CNN can significantly speed up the phase diagram calculations by predicting the final phase before the spin-lattice Monte Carlo sampling has converged. We show the prowess of this approach by generating phase diagrams with significantly shorter simulation times.