Optimal Equivariant Architectures from the Symmetries of Matrix-Element Likelihoods

The Matrix-Element Method (MEM) has long been a cornerstone of data analysis in high-energy physics. It leverages theoretical knowledge of parton-level processes and symmetries to evaluate the likelihood of observed events. In parallel, the advent of geometric deep learning has enabled neural network architectures that incorporate known symmetries directly into their design, leading to more efficient learning. This paper presents a novel approach that combines MEM-inspired symmetry considerations with equivariant neural network design for particle physics analysis. Even though Lorentz invariance and permutation invariance overall reconstructed objects are the largest and most natural symmetry in the input domain, we find that they are sub-optimal in most practical search scenarios. We propose a longitudinal boost-equivariant message-passing neural network architecture that preserves relevant discrete symmetries. We present numerical studies demonstrating MEM-inspired architectures achieve new state-of-the-art performance in distinguishing di-Higgs decays to four bottom quarks from the QCD background, with enhanced sample and parameter efficiencies. This synergy between MEM and equivariant deep learning opens new directions for physics-informed architecture design, promising more powerful tools for probing physics beyond the Standard Model.

Optimal Symmetries in Binary Classification

We explore the role of group symmetries in binary classification tasks, presenting a novel framework that leverages the principles of Neyman-Pearson optimality. Contrary to the common intuition that larger symmetry groups lead to improved classification performance, our findings show that selecting the appropriate group symmetries is crucial for optimising generalisation and sample efficiency. We develop a theoretical foundation for designing group equivariant neural networks that align the choice of symmetries with the underlying probability distributions of the data. Our approach provides a unified methodology for improving classification accuracy across a broad range of applications by carefully tailoring the symmetry group to the specific characteristics of the problem. Theoretical analysis and experimental results demonstrate that optimal classification performance is not always associated with the largest equivariant groups possible in the domain, even when the likelihood ratio is invariant under one of its proper subgroups, but rather with those subgroups themselves. This work offers insights and practical guidelines for constructing more effective group equivariant architectures in diverse machine-learning contexts.

IRC-safe Graph Autoencoder for an unsupervised anomaly detection

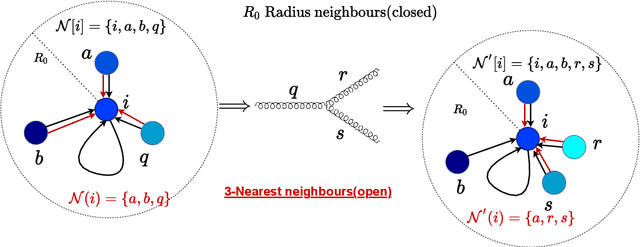
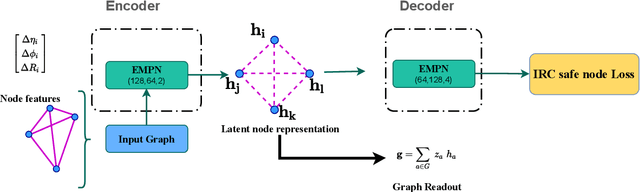
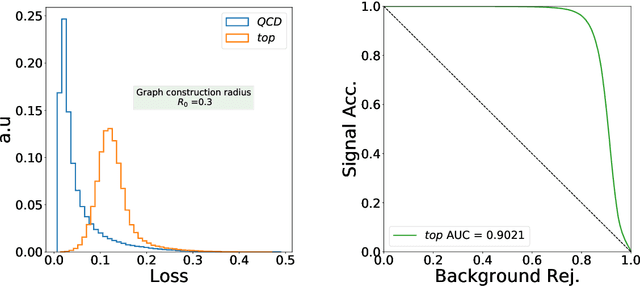
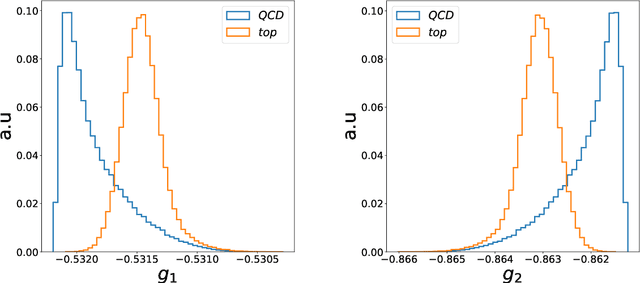
Anomaly detection through employing machine learning techniques has emerged as a novel powerful tool in the search for new physics beyond the Standard Model. Historically similar to the development of jet observables, theoretical consistency has not always assumed a central role in the fast development of algorithms and neural network architectures. In this work, we construct an infrared and collinear safe autoencoder based on graph neural networks by employing energy-weighted message passing. We demonstrate that whilst this approach has theoretically favourable properties, it also exhibits formidable sensitivity to non-QCD structures.