Quantum Annealing Feature Selection on Light-weight Medical Image Datasets

We investigate the use of quantum computing algorithms on real quantum hardware to tackle the computationally intensive task of feature selection for light-weight medical image datasets. Feature selection is often formulated as a k of n selection problem, where the complexity grows binomially with increasing k and n. As problem sizes grow, classical approaches struggle to scale efficiently. Quantum computers, particularly quantum annealers, are well-suited for such problems, offering potential advantages in specific formulations. We present a method to solve larger feature selection instances than previously presented on commercial quantum annealers. Our approach combines a linear Ising penalty mechanism with subsampling and thresholding techniques to enhance scalability. The method is tested in a toy problem where feature selection identifies pixel masks used to reconstruct small-scale medical images. The results indicate that quantum annealing-based feature selection is effective for this simplified use case, demonstrating its potential in high-dimensional optimization tasks. However, its applicability to broader, real-world problems remains uncertain, given the current limitations of quantum computing hardware.

Decoding Nature with Nature's Tools: Heterotic Line Bundle Models of Particle Physics with Genetic Algorithms and Quantum Annealing

The string theory landscape may include a multitude of ultraviolet embeddings of the Standard Model, but identifying these has proven difficult due to the enormous number of available string compactifications. Genetic Algorithms (GAs) represent a powerful class of discrete optimisation techniques that can efficiently deal with the immensity of the string landscape, especially when enhanced with input from quantum annealers. In this letter we focus on geometric compactifications of the $E_8\times E_8$ heterotic string theory compactified on smooth Calabi-Yau threefolds with Abelian bundles. We make use of analytic formulae for bundle-valued cohomology to impose the entire range of spectrum requirements, something that has not been possible so far. For manifolds with a relatively low number of Kahler parameters we compare the GA search results with results from previous systematic scans, showing that GAs can find nearly all the viable solutions while visiting only a tiny fraction of the solution space. Moreover, we carry out GA searches on manifolds with a larger numbers of Kahler parameters where systematic searches are not feasible.

A Genetic Quantum Annealing Algorithm

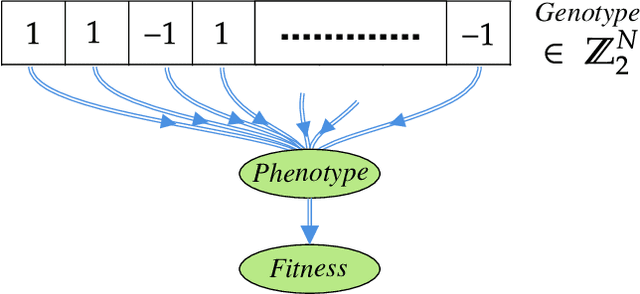
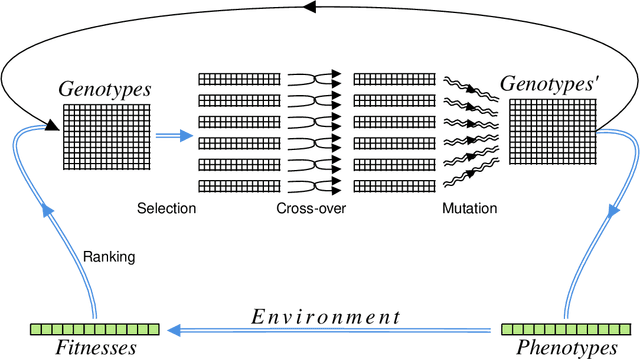
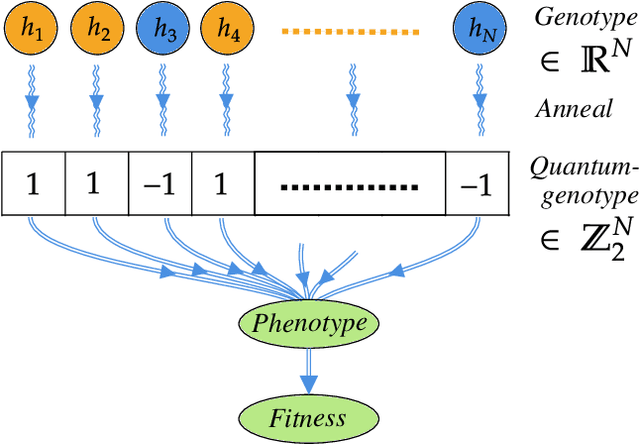
A genetic algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Natural Selection. We present an algorithm which enhances the classical GA with input from quantum annealers. As in a classical GA, the algorithm works by breeding a population of possible solutions based on their fitness. However, the population of individuals is defined by the continuous couplings on the quantum annealer, which then give rise via quantum annealing to the set of corresponding phenotypes that represent attempted solutions. This introduces a form of directed mutation into the algorithm that can enhance its performance in various ways. Two crucial enhancements come from the continuous couplings having strengths that are inherited from the fitness of the parents (so-called nepotism) and from the annealer couplings allowing the entire population to be influenced by the fittest individuals (so-called quantum-polyandry). We find our algorithm to be significantly more powerful on several simple problems than a classical GA.