A Genetic Quantum Annealing Algorithm
Paper and Code
Sep 15, 2022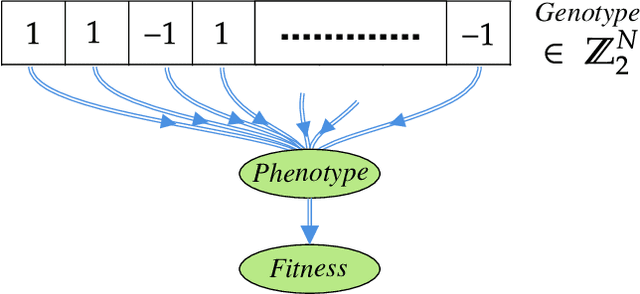
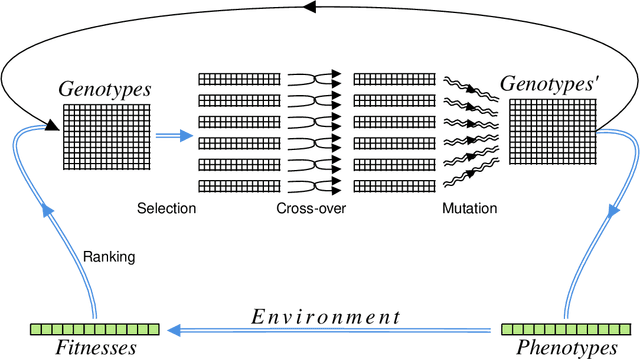
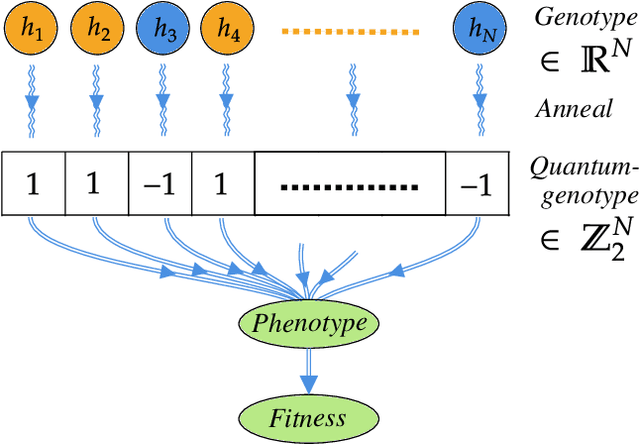

A genetic algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Natural Selection. We present an algorithm which enhances the classical GA with input from quantum annealers. As in a classical GA, the algorithm works by breeding a population of possible solutions based on their fitness. However, the population of individuals is defined by the continuous couplings on the quantum annealer, which then give rise via quantum annealing to the set of corresponding phenotypes that represent attempted solutions. This introduces a form of directed mutation into the algorithm that can enhance its performance in various ways. Two crucial enhancements come from the continuous couplings having strengths that are inherited from the fitness of the parents (so-called nepotism) and from the annealer couplings allowing the entire population to be influenced by the fittest individuals (so-called quantum-polyandry). We find our algorithm to be significantly more powerful on several simple problems than a classical GA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge