Symbolic Regression and Differentiable Fits in Beyond the Standard Model Physics

We demonstrate the efficacy of symbolic regression (SR) to probe models of particle physics Beyond the Standard Model (BSM), by considering the so-called Constrained Minimal Supersymmetric Standard Model (CMSSM). Like many incarnations of BSM physics this model has a number (four) of arbitrary parameters, which determine the experimental signals, and cosmological observables such as the dark matter relic density. We show that analysis of the phenomenology can be greatly accelerated by using symbolic expressions derived for the observables in terms of the input parameters. Here we focus on the Higgs mass, the cold dark matter relic density, and the contribution to the anomalous magnetic moment of the muon. We find that SR can produce remarkably accurate expressions. Using them we make global fits to derive the posterior probability densities of the CMSSM input parameters which are in good agreement with those performed using conventional methods. Moreover, we demonstrate a major advantage of SR which is the ability to make fits using differentiable methods rather than sampling methods. We also compare the method with neural network (NN) regression. SR produces more globally robust results, while NNs require data that is focussed on the promising regions in order to be equally performant.

A Genetic Quantum Annealing Algorithm

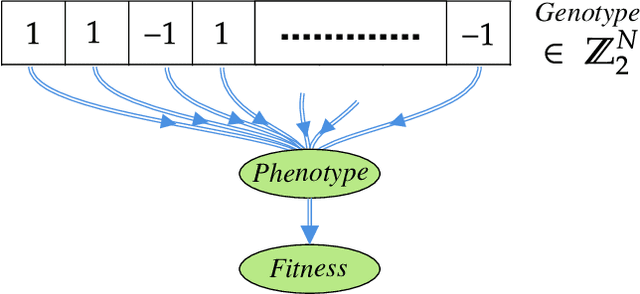
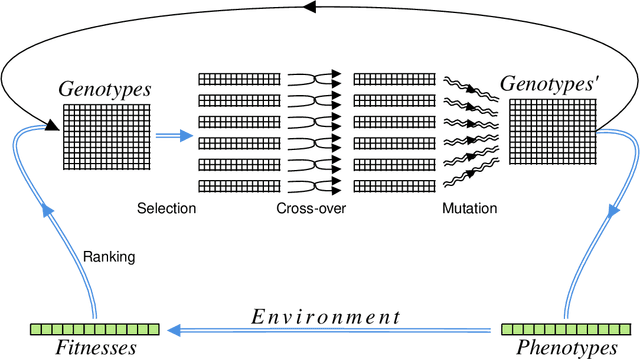
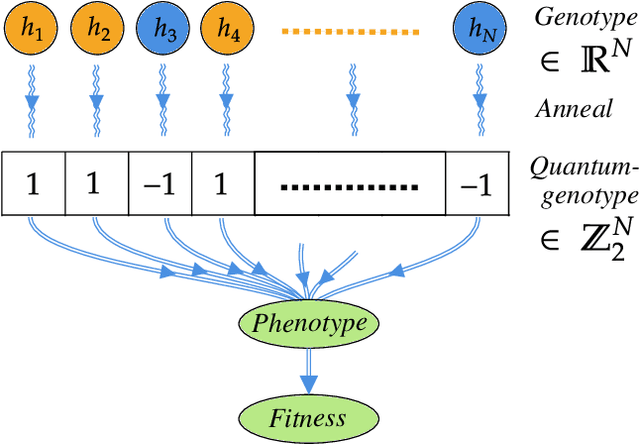
A genetic algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Natural Selection. We present an algorithm which enhances the classical GA with input from quantum annealers. As in a classical GA, the algorithm works by breeding a population of possible solutions based on their fitness. However, the population of individuals is defined by the continuous couplings on the quantum annealer, which then give rise via quantum annealing to the set of corresponding phenotypes that represent attempted solutions. This introduces a form of directed mutation into the algorithm that can enhance its performance in various ways. Two crucial enhancements come from the continuous couplings having strengths that are inherited from the fitness of the parents (so-called nepotism) and from the annealer couplings allowing the entire population to be influenced by the fittest individuals (so-called quantum-polyandry). We find our algorithm to be significantly more powerful on several simple problems than a classical GA.

The Power of Genetic Algorithms: what remains of the pMSSM?

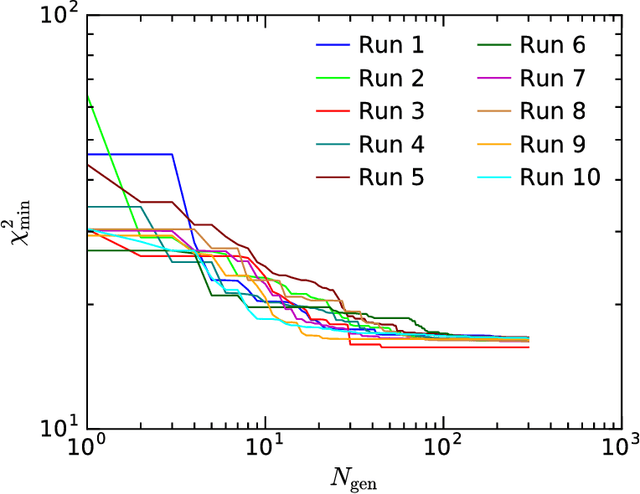
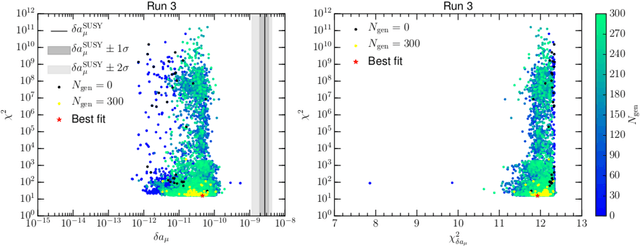
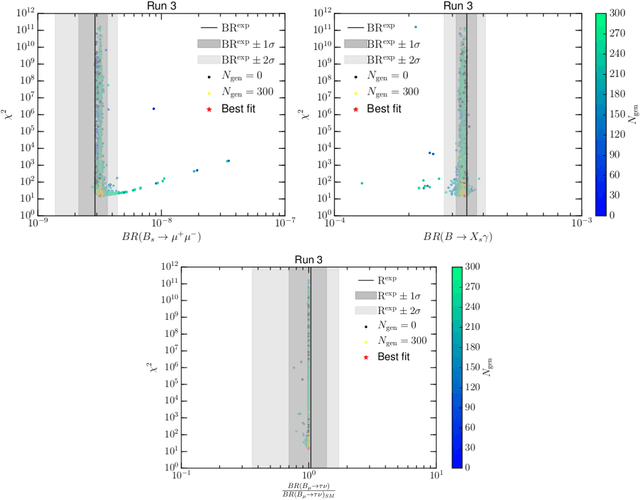
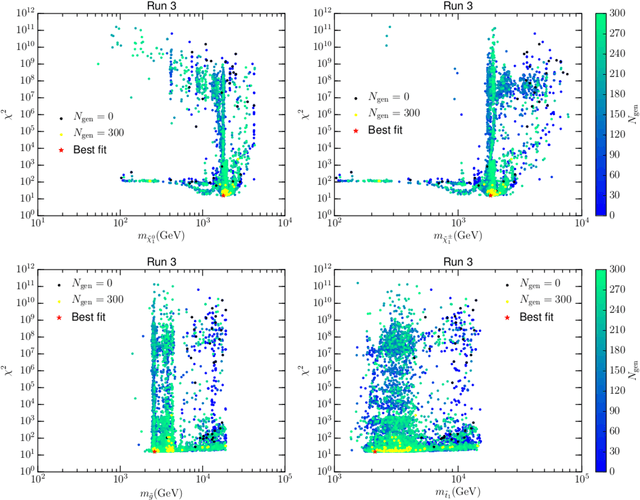
Genetic Algorithms (GAs) are explored as a tool for probing new physics with high dimensionality. We study the 19-dimensional pMSSM, including experimental constraints from all sources and assessing the consistency of potential signals of new physics. We show that GAs excel at making a fast and accurate diagnosis of the cross-compatibility of a set of experimental constraints in such high dimensional models. In the case of the pMSSM, it is found that only ${\cal O}(10^4)$ model evaluations are required to obtain a best fit point in agreement with much more costly MCMC scans. This efficiency allows higher dimensional models to be falsified, and patterns in the spectrum identified, orders of magnitude more quickly. As examples of falsification, we consider the muon anomalous magnetic moment, and the Galactic Centre gamma-ray excess observed by Fermi-LAT, which could in principle be explained in terms of neutralino dark matter. We show that both observables cannot be explained within the pMSSM, and that they provide the leading contribution to the total goodness of the fit, with $\chi^2_{\delta a_\mu^{\mathrm{SUSY}}}\approx12$ and $\chi^2_{\rm GCE}\approx 155$, respectively.