Thomas R. Harvey
The Optimiser Hidden in Plain Sight: Training with the Loss Landscape's Induced Metric
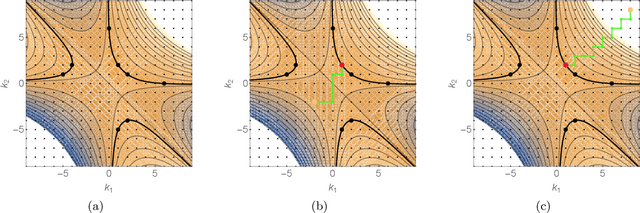
Sep 03, 2025Abstract:We present a class of novel optimisers for training neural networks that makes use of the Riemannian metric naturally induced when the loss landscape is embedded in higher-dimensional space. This is the same metric that underlies common visualisations of loss landscapes. By taking this geometric perspective literally and using the induced metric, we develop a new optimiser and compare it to existing methods, namely: SGD, Adam, AdamW, and Muon, across a range of tasks and architectures. Empirically, we conclude that this new class of optimisers is highly effective in low dimensional examples, and provides slight improvement over state-of-the-art methods for training neural networks. These new optimisers have theoretically desirable properties. In particular, the effective learning rate is automatically decreased in regions of high curvature acting as a smoothed out form of gradient clipping. Similarly, one variant of these optimisers can also be viewed as inducing an effective scheduled learning rate and decoupled weight decay is the natural choice from our geometric perspective. The basic method can be used to modify any existing preconditioning method. The new optimiser has a computational complexity comparable to that of Adam.
Symbolic Regression with Multimodal Large Language Models and Kolmogorov Arnold Networks
May 12, 2025Abstract:We present a novel approach to symbolic regression using vision-capable large language models (LLMs) and the ideas behind Google DeepMind's Funsearch. The LLM is given a plot of a univariate function and tasked with proposing an ansatz for that function. The free parameters of the ansatz are fitted using standard numerical optimisers, and a collection of such ans\"atze make up the population of a genetic algorithm. Unlike other symbolic regression techniques, our method does not require the specification of a set of functions to be used in regression, but with appropriate prompt engineering, we can arbitrarily condition the generative step. By using Kolmogorov Arnold Networks (KANs), we demonstrate that ``univariate is all you need'' for symbolic regression, and extend this method to multivariate functions by learning the univariate function on each edge of a trained KAN. The combined expression is then simplified by further processing with a language model.
Generative Modeling for Mathematical Discovery
Mar 17, 2025Abstract:We present a new implementation of the LLM-driven genetic algorithm {\it funsearch}, whose aim is to generate examples of interest to mathematicians and which has already had some success in problems in extremal combinatorics. Our implementation is designed to be useful in practice for working mathematicians; it does not require expertise in machine learning or access to high-performance computing resources. Applying {\it funsearch} to a new problem involves modifying a small segment of Python code and selecting a large language model (LLM) from one of many third-party providers. We benchmarked our implementation on three different problems, obtaining metrics that may inform applications of {\it funsearch} to new problems. Our results demonstrate that {\it funsearch} successfully learns in a variety of combinatorial and number-theoretic settings, and in some contexts learns principles that generalize beyond the problem originally trained on.
Decoding Nature with Nature's Tools: Heterotic Line Bundle Models of Particle Physics with Genetic Algorithms and Quantum Annealing
Jun 05, 2023Abstract:The string theory landscape may include a multitude of ultraviolet embeddings of the Standard Model, but identifying these has proven difficult due to the enormous number of available string compactifications. Genetic Algorithms (GAs) represent a powerful class of discrete optimisation techniques that can efficiently deal with the immensity of the string landscape, especially when enhanced with input from quantum annealers. In this letter we focus on geometric compactifications of the $E_8\times E_8$ heterotic string theory compactified on smooth Calabi-Yau threefolds with Abelian bundles. We make use of analytic formulae for bundle-valued cohomology to impose the entire range of spectrum requirements, something that has not been possible so far. For manifolds with a relatively low number of Kahler parameters we compare the GA search results with results from previous systematic scans, showing that GAs can find nearly all the viable solutions while visiting only a tiny fraction of the solution space. Moreover, we carry out GA searches on manifolds with a larger numbers of Kahler parameters where systematic searches are not feasible.
Heterotic String Model Building with Monad Bundles and Reinforcement Learning
Aug 16, 2021


Abstract:We use reinforcement learning as a means of constructing string compactifications with prescribed properties. Specifically, we study heterotic SO(10) GUT models on Calabi-Yau three-folds with monad bundles, in search of phenomenologically promising examples. Due to the vast number of bundles and the sparseness of viable choices, methods based on systematic scanning are not suitable for this class of models. By focusing on two specific manifolds with Picard numbers two and three, we show that reinforcement learning can be used successfully to explore monad bundles. Training can be accomplished with minimal computing resources and leads to highly efficient policy networks. They produce phenomenologically promising states for nearly 100% of episodes and within a small number of steps. In this way, hundreds of new candidate standard models are found.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge