Generative Modeling for Mathematical Discovery

We present a new implementation of the LLM-driven genetic algorithm {\it funsearch}, whose aim is to generate examples of interest to mathematicians and which has already had some success in problems in extremal combinatorics. Our implementation is designed to be useful in practice for working mathematicians; it does not require expertise in machine learning or access to high-performance computing resources. Applying {\it funsearch} to a new problem involves modifying a small segment of Python code and selecting a large language model (LLM) from one of many third-party providers. We benchmarked our implementation on three different problems, obtaining metrics that may inform applications of {\it funsearch} to new problems. Our results demonstrate that {\it funsearch} successfully learns in a variety of combinatorial and number-theoretic settings, and in some contexts learns principles that generalize beyond the problem originally trained on.

PatternBoost: Constructions in Mathematics with a Little Help from AI

We introduce PatternBoost, a flexible method for finding interesting constructions in mathematics. Our algorithm alternates between two phases. In the first ``local'' phase, a classical search algorithm is used to produce many desirable constructions. In the second ``global'' phase, a transformer neural network is trained on the best such constructions. Samples from the trained transformer are then used as seeds for the first phase, and the process is repeated. We give a detailed introduction to this technique, and discuss the results of its application to several problems in extremal combinatorics. The performance of PatternBoost varies across different problems, but there are many situations where its performance is quite impressive. Using our technique, we find the best known solutions to several long-standing problems, including the construction of a counterexample to a conjecture that had remained open for 30 years.

Convergence rates for ordinal embedding

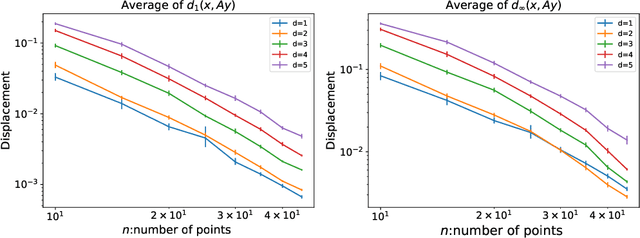
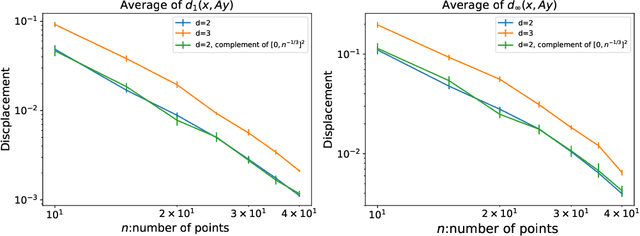
We prove optimal bounds for the convergence rate of ordinal embedding (also known as non-metric multidimensional scaling) in the 1-dimensional case. The examples witnessing optimality of our bounds arise from a result in additive number theory on sets of integers with no three-term arithmetic progressions. We also carry out some computational experiments aimed at developing a sense of what the convergence rate for ordinal embedding might look like in higher dimensions.

Detection of Planted Solutions for Flat Satisfiability Problems

We study the detection problem of finding planted solutions in random instances of flat satisfiability problems, a generalization of boolean satisfiability formulas. We describe the properties of random instances of flat satisfiability, as well of the optimal rates of detection of the associated hypothesis testing problem. We also study the performance of an algorithmically efficient testing procedure. We introduce a modification of our model, the light planting of solutions, and show that it is as hard as the problem of learning parity with noise. This hints strongly at the difficulty of detecting planted flat satisfiability for a wide class of tests.