Control Variate Score Matching for Diffusion Models

Diffusion models offer a robust framework for sampling from unnormalized probability densities, which requires accurately estimating the score of the noise-perturbed target distribution. While the standard Denoising Score Identity (DSI) relies on data samples, access to the target energy function enables an alternative formulation via the Target Score Identity (TSI). However, these estimators face a fundamental variance trade-off: DSI exhibits high variance in low-noise regimes, whereas TSI suffers from high variance at high noise levels. In this work, we reconcile these approaches by unifying both estimators within the principled framework of control variates. We introduce the Control Variate Score Identity (CVSI), deriving an optimal, time-dependent control coefficient that theoretically guarantees variance minimization across the entire noise spectrum. We demonstrate that CVSI serves as a robust, low-variance plug-in estimator that significantly enhances sample efficiency in both data-free sampler learning and inference-time diffusion sampling.

Building Bridges between Regression, Clustering, and Classification

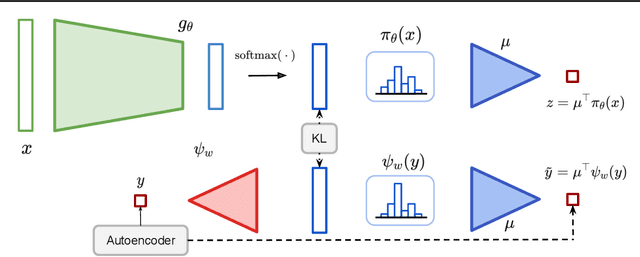
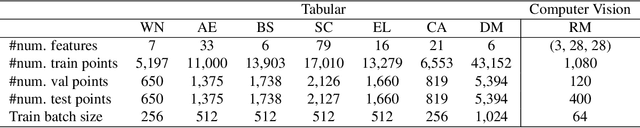
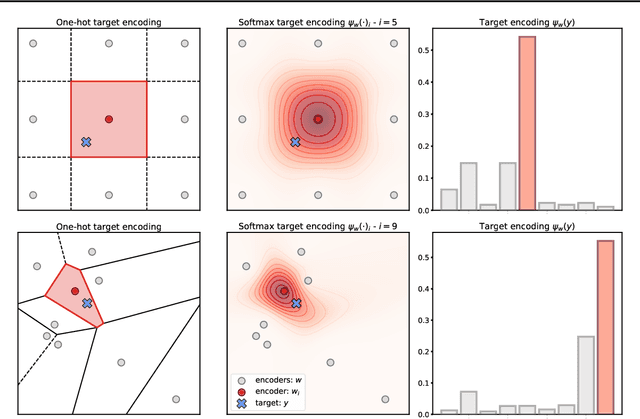
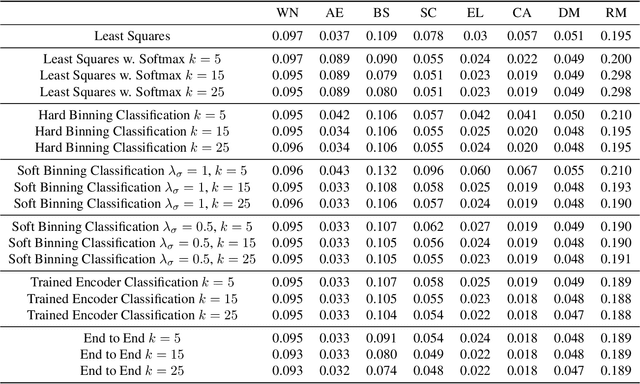
Regression, the task of predicting a continuous scalar target y based on some features x is one of the most fundamental tasks in machine learning and statistics. It has been observed and theoretically analyzed that the classical approach, meansquared error minimization, can lead to suboptimal results when training neural networks. In this work, we propose a new method to improve the training of these models on regression tasks, with continuous scalar targets. Our method is based on casting this task in a different fashion, using a target encoder, and a prediction decoder, inspired by approaches in classification and clustering. We showcase the performance of our method on a wide range of real-world datasets.

Soft Condorcet Optimization for Ranking of General Agents

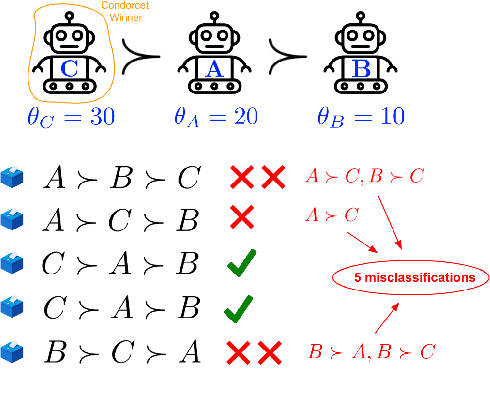
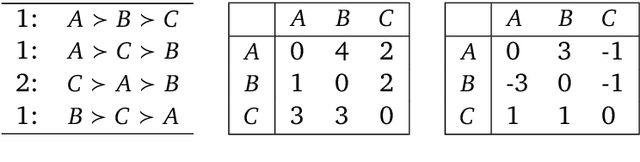
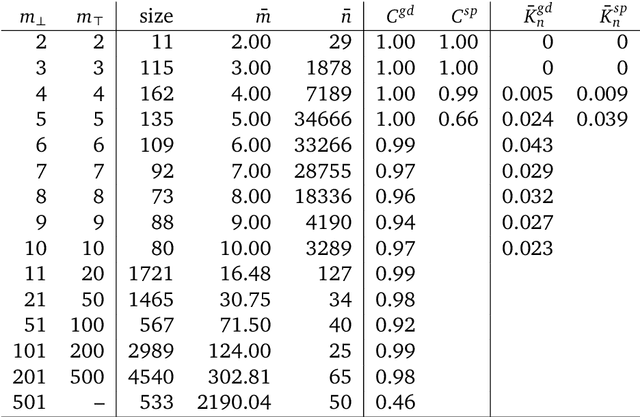
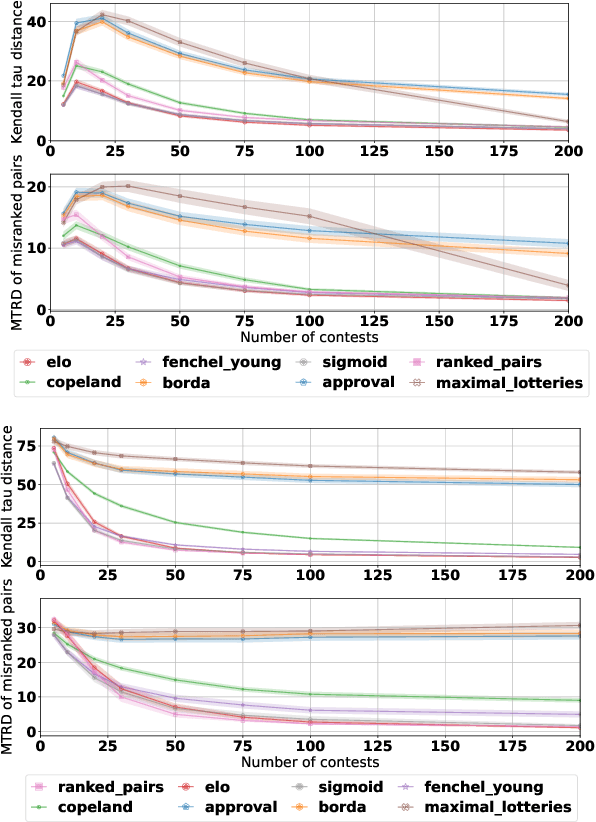
A common way to drive progress of AI models and agents is to compare their performance on standardized benchmarks. Comparing the performance of general agents requires aggregating their individual performances across a potentially wide variety of different tasks. In this paper, we describe a novel ranking scheme inspired by social choice frameworks, called Soft Condorcet Optimization (SCO), to compute the optimal ranking of agents: the one that makes the fewest mistakes in predicting the agent comparisons in the evaluation data. This optimal ranking is the maximum likelihood estimate when evaluation data (which we view as votes) are interpreted as noisy samples from a ground truth ranking, a solution to Condorcet's original voting system criteria. SCO ratings are maximal for Condorcet winners when they exist, which we show is not necessarily true for the classical rating system Elo. We propose three optimization algorithms to compute SCO ratings and evaluate their empirical performance. When serving as an approximation to the Kemeny-Young voting method, SCO rankings are on average 0 to 0.043 away from the optimal ranking in normalized Kendall-tau distance across 865 preference profiles from the PrefLib open ranking archive. In a simulated noisy tournament setting, SCO achieves accurate approximations to the ground truth ranking and the best among several baselines when 59\% or more of the preference data is missing. Finally, SCO ranking provides the best approximation to the optimal ranking, measured on held-out test sets, in a problem containing 52,958 human players across 31,049 games of the classic seven-player game of Diplomacy.

Implicit Diffusion: Efficient Optimization through Stochastic Sampling

We present a new algorithm to optimize distributions defined implicitly by parameterized stochastic diffusions. Doing so allows us to modify the outcome distribution of sampling processes by optimizing over their parameters. We introduce a general framework for first-order optimization of these processes, that performs jointly, in a single loop, optimization and sampling steps. This approach is inspired by recent advances in bilevel optimization and automatic implicit differentiation, leveraging the point of view of sampling as optimization over the space of probability distributions. We provide theoretical guarantees on the performance of our method, as well as experimental results demonstrating its effectiveness in real-world settings.

Decoding-time Realignment of Language Models

Aligning language models with human preferences is crucial for reducing errors and biases in these models. Alignment techniques, such as reinforcement learning from human feedback (RLHF), are typically cast as optimizing a tradeoff between human preference rewards and a proximity regularization term that encourages staying close to the unaligned model. Selecting an appropriate level of regularization is critical: insufficient regularization can lead to reduced model capabilities due to reward hacking, whereas excessive regularization hinders alignment. Traditional methods for finding the optimal regularization level require retraining multiple models with varying regularization strengths. This process, however, is resource-intensive, especially for large models. To address this challenge, we propose decoding-time realignment (DeRa), a simple method to explore and evaluate different regularization strengths in aligned models without retraining. DeRa enables control over the degree of alignment, allowing users to smoothly transition between unaligned and aligned models. It also enhances the efficiency of hyperparameter tuning by enabling the identification of effective regularization strengths using a validation dataset.

Differentiable Clustering with Perturbed Spanning Forests

We introduce a differentiable clustering method based on minimum-weight spanning forests, a variant of spanning trees with several connected components. Our method relies on stochastic perturbations of solutions of linear programs, for smoothing and efficient gradient computations. This allows us to include clustering in end-to-end trainable pipelines. We show that our method performs well even in difficult settings, such as datasets with high noise and challenging geometries. We also formulate an ad hoc loss to efficiently learn from partial clustering data using this operation. We demonstrate its performance on several real world datasets for supervised and semi-supervised tasks.

Mirror Sinkhorn: Fast Online Optimization on Transport Polytopes

Optimal transport has arisen as an important tool in machine learning, allowing to capture geometric properties of the data. It is formulated as a linear program on transport polytopes. The problem of convex optimization on this set includes both OT and multiple related ones, such as point cloud registration. We present in this work an optimization algorithm that utilizes Sinkhorn matrix scaling and mirror descent to minimize convex objectives on this domain. This algorithm can be run online and is both adaptive and robust to noise. A mathematical analysis of the convergence rate of the algorithm for minimising convex functions is provided, as well as experiments that illustrate its performance on synthetic data and real-world data.

Regression as Classification: Influence of Task Formulation on Neural Network Features

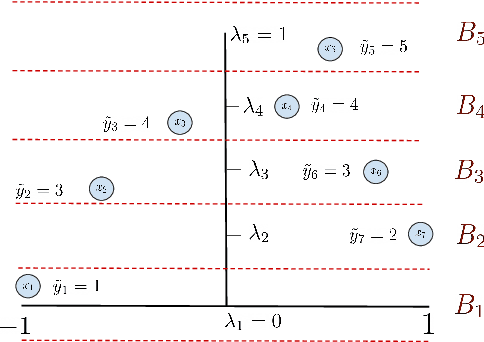
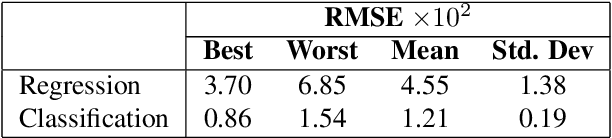
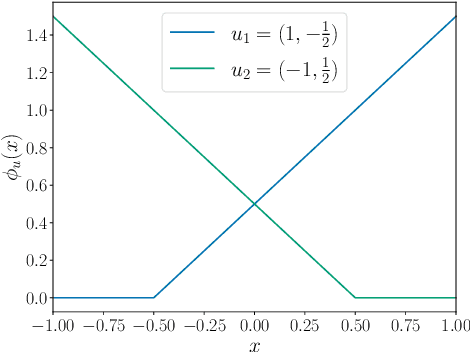
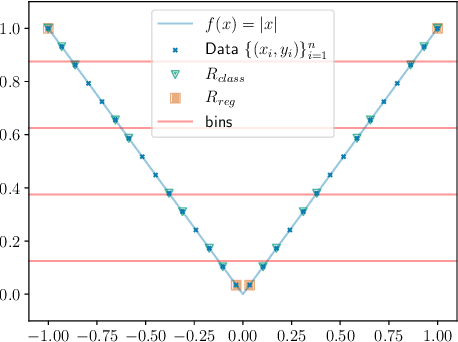
Neural networks can be trained to solve regression problems by using gradient-based methods to minimize the square loss. However, practitioners often prefer to reformulate regression as a classification problem, observing that training on the cross entropy loss results in better performance. By focusing on two-layer ReLU networks, which can be fully characterized by measures over their feature space, we explore how the implicit bias induced by gradient-based optimization could partly explain the above phenomenon. We provide theoretical evidence that the regression formulation yields a measure whose support can differ greatly from that for classification, in the case of one-dimensional data. Our proposed optimal supports correspond directly to the features learned by the input layer of the network. The different nature of these supports sheds light on possible optimization difficulties the square loss could encounter during training, and we present empirical results illustrating this phenomenon.

Fast Stochastic Composite Minimization and an Accelerated Frank-Wolfe Algorithm under Parallelization

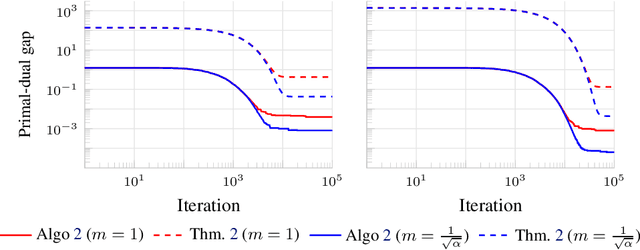
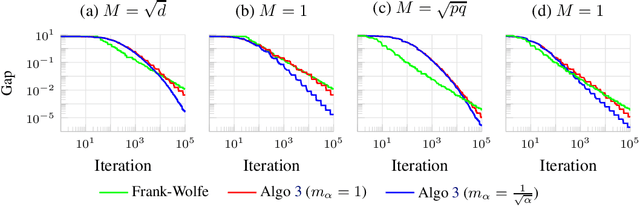
We consider the problem of minimizing the sum of two convex functions. One of those functions has Lipschitz-continuous gradients, and can be accessed via stochastic oracles, whereas the other is "simple". We provide a Bregman-type algorithm with accelerated convergence in function values to a ball containing the minimum. The radius of this ball depends on problem-dependent constants, including the variance of the stochastic oracle. We further show that this algorithmic setup naturally leads to a variant of Frank-Wolfe achieving acceleration under parallelization. More precisely, when minimizing a smooth convex function on a bounded domain, we show that one can achieve an $\epsilon$ primal-dual gap (in expectation) in $\tilde{O}(1/ \sqrt{\epsilon})$ iterations, by only accessing gradients of the original function and a linear maximization oracle with $O(1/\sqrt{\epsilon})$ computing units in parallel. We illustrate this fast convergence on synthetic numerical experiments.

A unified software/hardware scalable architecture for brain-inspired computing based on self-organizing neural models

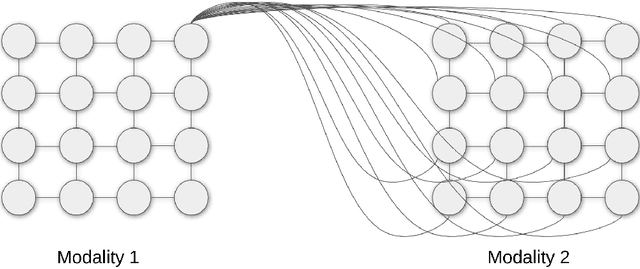
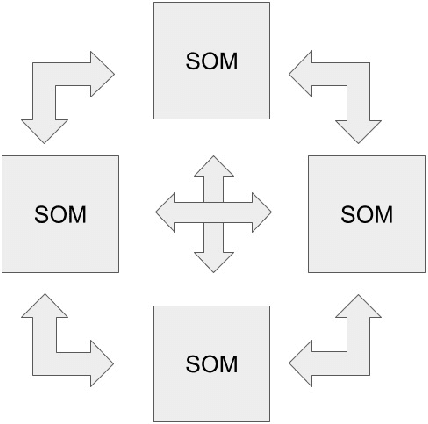
The field of artificial intelligence has significantly advanced over the past decades, inspired by discoveries from the fields of biology and neuroscience. The idea of this work is inspired by the process of self-organization of cortical areas in the human brain from both afferent and lateral/internal connections. In this work, we develop an original brain-inspired neural model associating Self-Organizing Maps (SOM) and Hebbian learning in the Reentrant SOM (ReSOM) model. The framework is applied to multimodal classification problems. Compared to existing methods based on unsupervised learning with post-labeling, the model enhances the state-of-the-art results. This work also demonstrates the distributed and scalable nature of the model through both simulation results and hardware execution on a dedicated FPGA-based platform named SCALP (Self-configurable 3D Cellular Adaptive Platform). SCALP boards can be interconnected in a modular way to support the structure of the neural model. Such a unified software and hardware approach enables the processing to be scaled and allows information from several modalities to be merged dynamically. The deployment on hardware boards provides performance results of parallel execution on several devices, with the communication between each board through dedicated serial links. The proposed unified architecture, composed of the ReSOM model and the SCALP hardware platform, demonstrates a significant increase in accuracy thanks to multimodal association, and a good trade-off between latency and power consumption compared to a centralized GPU implementation.