Soft Condorcet Optimization for Ranking of General Agents

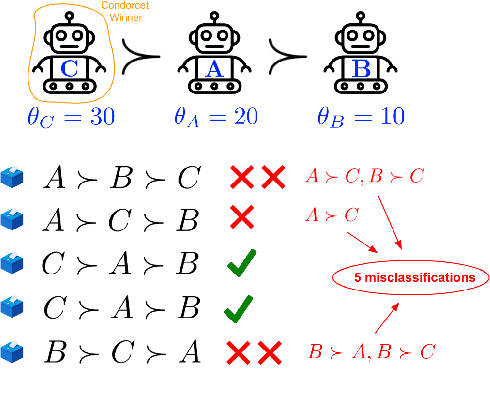
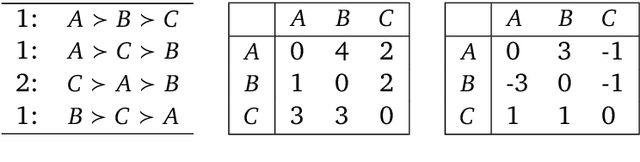
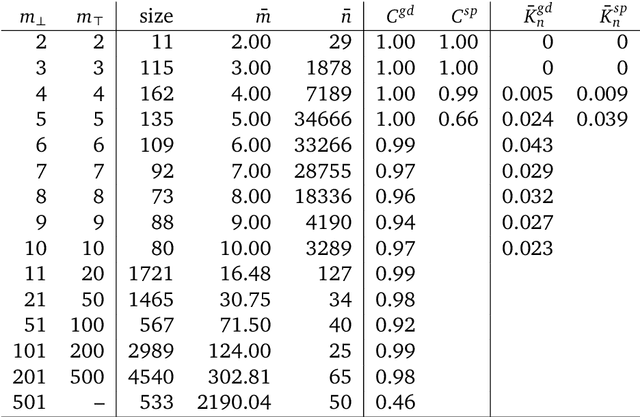
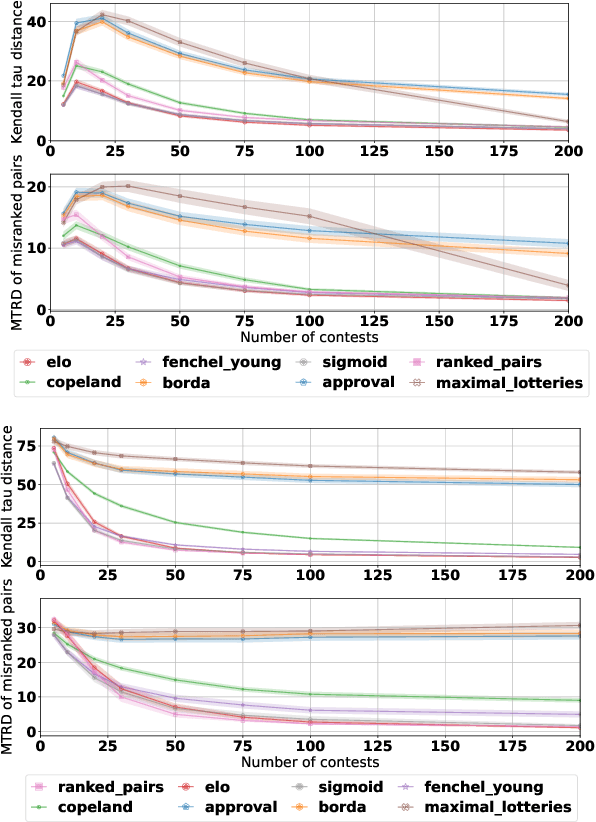
A common way to drive progress of AI models and agents is to compare their performance on standardized benchmarks. Comparing the performance of general agents requires aggregating their individual performances across a potentially wide variety of different tasks. In this paper, we describe a novel ranking scheme inspired by social choice frameworks, called Soft Condorcet Optimization (SCO), to compute the optimal ranking of agents: the one that makes the fewest mistakes in predicting the agent comparisons in the evaluation data. This optimal ranking is the maximum likelihood estimate when evaluation data (which we view as votes) are interpreted as noisy samples from a ground truth ranking, a solution to Condorcet's original voting system criteria. SCO ratings are maximal for Condorcet winners when they exist, which we show is not necessarily true for the classical rating system Elo. We propose three optimization algorithms to compute SCO ratings and evaluate their empirical performance. When serving as an approximation to the Kemeny-Young voting method, SCO rankings are on average 0 to 0.043 away from the optimal ranking in normalized Kendall-tau distance across 865 preference profiles from the PrefLib open ranking archive. In a simulated noisy tournament setting, SCO achieves accurate approximations to the ground truth ranking and the best among several baselines when 59\% or more of the preference data is missing. Finally, SCO ranking provides the best approximation to the optimal ranking, measured on held-out test sets, in a problem containing 52,958 human players across 31,049 games of the classic seven-player game of Diplomacy.