Ian Gemp
Active Evaluation of General Agents: Problem Definition and Comparison of Baseline Algorithms
Jan 12, 2026Abstract:As intelligent agents become more generally-capable, i.e. able to master a wide variety of tasks, the complexity and cost of properly evaluating them rises significantly. Tasks that assess specific capabilities of the agents can be correlated and stochastic, requiring many samples for accurate comparisons, leading to added costs. In this paper, we propose a formal definition and a conceptual framework for active evaluation of agents across multiple tasks, which assesses the performance of ranking algorithms as a function of number of evaluation data samples. Rather than curating, filtering, or compressing existing data sets as a preprocessing step, we propose an online framing: on every iteration, the ranking algorithm chooses the task and agents to sample scores from. Then, evaluation algorithms report a ranking of agents on each iteration and their performance is assessed with respect to the ground truth ranking over time. Several baselines are compared under different experimental contexts, with synthetic generated data and simulated online access to real evaluation data from Atari game-playing agents. We find that the classical Elo rating system -- while it suffers from well-known failure modes, in theory -- is a consistently reliable choice for efficient reduction of ranking error in practice. A recently-proposed method, Soft Condorcet Optimization, shows comparable performance to Elo on synthetic data and significantly outperforms Elo on real Atari agent evaluation. When task variation from the ground truth is high, selecting tasks based on proportional representation leads to higher rate of ranking error reduction.
Code World Models for General Game Playing
Oct 06, 2025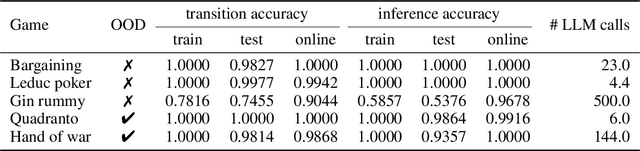

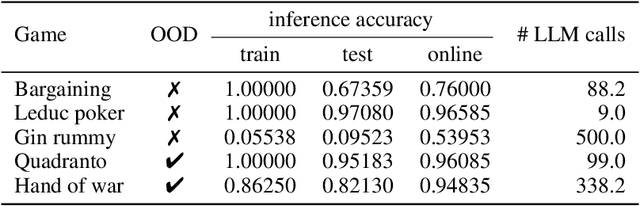
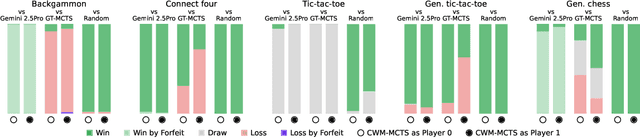
Abstract:Large Language Models (LLMs) reasoning abilities are increasingly being applied to classical board and card games, but the dominant approach -- involving prompting for direct move generation -- has significant drawbacks. It relies on the model's implicit fragile pattern-matching capabilities, leading to frequent illegal moves and strategically shallow play. Here we introduce an alternative approach: We use the LLM to translate natural language rules and game trajectories into a formal, executable world model represented as Python code. This generated model -- comprising functions for state transition, legal move enumeration, and termination checks -- serves as a verifiable simulation engine for high-performance planning algorithms like Monte Carlo tree search (MCTS). In addition, we prompt the LLM to generate heuristic value functions (to make MCTS more efficient), and inference functions (to estimate hidden states in imperfect information games). Our method offers three distinct advantages compared to directly using the LLM as a policy: (1) Verifiability: The generated CWM serves as a formal specification of the game's rules, allowing planners to algorithmically enumerate valid actions and avoid illegal moves, contingent on the correctness of the synthesized model; (2) Strategic Depth: We combine LLM semantic understanding with the deep search power of classical planners; and (3) Generalization: We direct the LLM to focus on the meta-task of data-to-code translation, enabling it to adapt to new games more easily. We evaluate our agent on 10 different games, of which 4 are novel and created for this paper. 5 of the games are fully observed (perfect information), and 5 are partially observed (imperfect information). We find that our method outperforms or matches Gemini 2.5 Pro in 9 out of the 10 considered games.
LLM-Mediated Guidance of MARL Systems
Mar 16, 2025Abstract:In complex multi-agent environments, achieving efficient learning and desirable behaviours is a significant challenge for Multi-Agent Reinforcement Learning (MARL) systems. This work explores the potential of combining MARL with Large Language Model (LLM)-mediated interventions to guide agents toward more desirable behaviours. Specifically, we investigate how LLMs can be used to interpret and facilitate interventions that shape the learning trajectories of multiple agents. We experimented with two types of interventions, referred to as controllers: a Natural Language (NL) Controller and a Rule-Based (RB) Controller. The NL Controller, which uses an LLM to simulate human-like interventions, showed a stronger impact than the RB Controller. Our findings indicate that agents particularly benefit from early interventions, leading to more efficient training and higher performance. Both intervention types outperform the baseline without interventions, highlighting the potential of LLM-mediated guidance to accelerate training and enhance MARL performance in challenging environments.
Re-evaluating Open-ended Evaluation of Large Language Models
Feb 27, 2025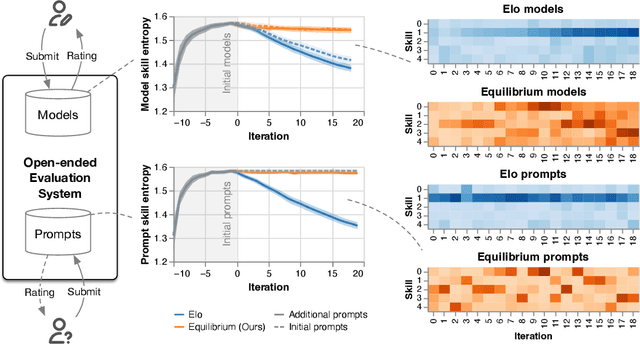

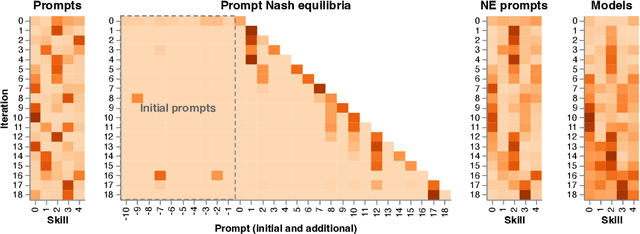
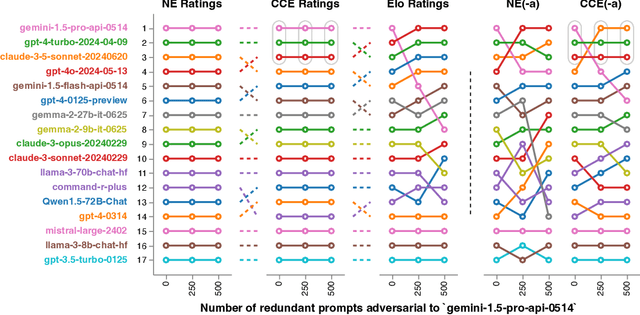
Abstract:Evaluation has traditionally focused on ranking candidates for a specific skill. Modern generalist models, such as Large Language Models (LLMs), decidedly outpace this paradigm. Open-ended evaluation systems, where candidate models are compared on user-submitted prompts, have emerged as a popular solution. Despite their many advantages, we show that the current Elo-based rating systems can be susceptible to and even reinforce biases in data, intentional or accidental, due to their sensitivity to redundancies. To address this issue, we propose evaluation as a 3-player game, and introduce novel game-theoretic solution concepts to ensure robustness to redundancy. We show that our method leads to intuitive ratings and provide insights into the competitive landscape of LLM development.
Deviation Ratings: A General, Clone-Invariant Rating Method
Feb 17, 2025Abstract:Many real-world multi-agent or multi-task evaluation scenarios can be naturally modelled as normal-form games due to inherent strategic (adversarial, cooperative, and mixed motive) interactions. These strategic interactions may be agentic (e.g. players trying to win), fundamental (e.g. cost vs quality), or complementary (e.g. niche finding and specialization). In such a formulation, it is the strategies (actions, policies, agents, models, tasks, prompts, etc.) that are rated. However, the rating problem is complicated by redundancy and complexity of N-player strategic interactions. Repeated or similar strategies can distort ratings for those that counter or complement them. Previous work proposed ``clone invariant'' ratings to handle such redundancies, but this was limited to two-player zero-sum (i.e. strictly competitive) interactions. This work introduces the first N-player general-sum clone invariant rating, called deviation ratings, based on coarse correlated equilibria. The rating is explored on several domains including LLMs evaluation.
Charting the Shapes of Stories with Game Theory
Dec 07, 2024Abstract:Stories are records of our experiences and their analysis reveals insights into the nature of being human. Successful analyses are often interdisciplinary, leveraging mathematical tools to extract structure from stories and insights from structure. Historically, these tools have been restricted to one dimensional charts and dynamic social networks; however, modern AI offers the possibility of identifying more fully the plot structure, character incentives, and, importantly, counterfactual plot lines that the story could have taken but did not take. In this work, we use AI to model the structure of stories as game-theoretic objects, amenable to quantitative analysis. This allows us to not only interrogate each character's decision making, but also possibly peer into the original author's conception of the characters' world. We demonstrate our proposed technique on Shakespeare's famous Romeo and Juliet. We conclude with a discussion of how our analysis could be replicated in broader contexts, including real-life scenarios.
Nash Equilibria via Stochastic Eigendecomposition
Nov 04, 2024Abstract:This work proposes a novel set of techniques for approximating a Nash equilibrium in a finite, normal-form game. It achieves this by constructing a new reformulation as solving a parameterized system of multivariate polynomials with tunable complexity. In doing so, it forges an itinerant loop from game theory to machine learning and back. We show a Nash equilibrium can be approximated with purely calls to stochastic, iterative variants of singular value decomposition and power iteration, with implications for biological plausibility. We provide pseudocode and experiments demonstrating solving for all equilibria of a general-sum game using only these readily available linear algebra tools.
Soft Condorcet Optimization for Ranking of General Agents
Nov 04, 2024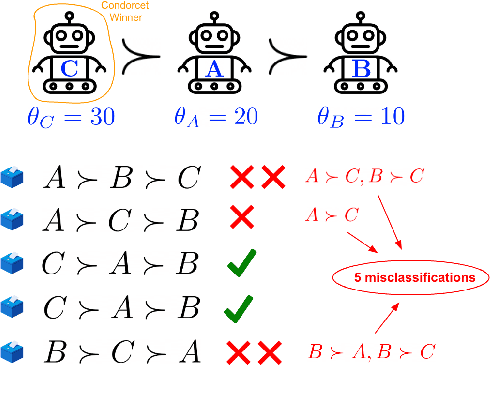
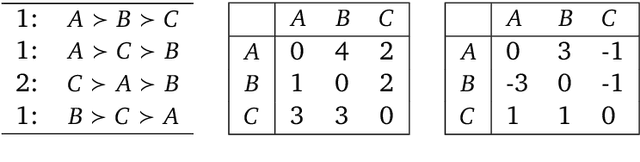
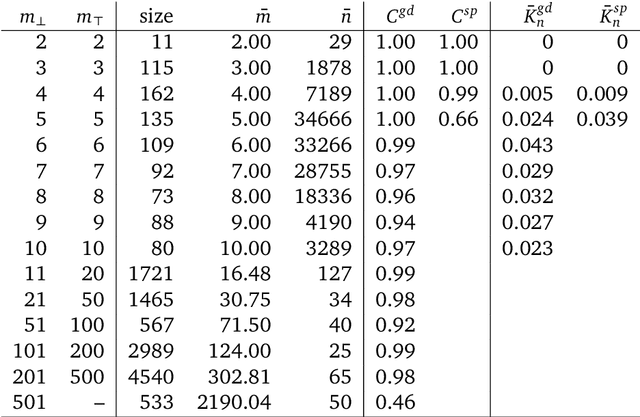
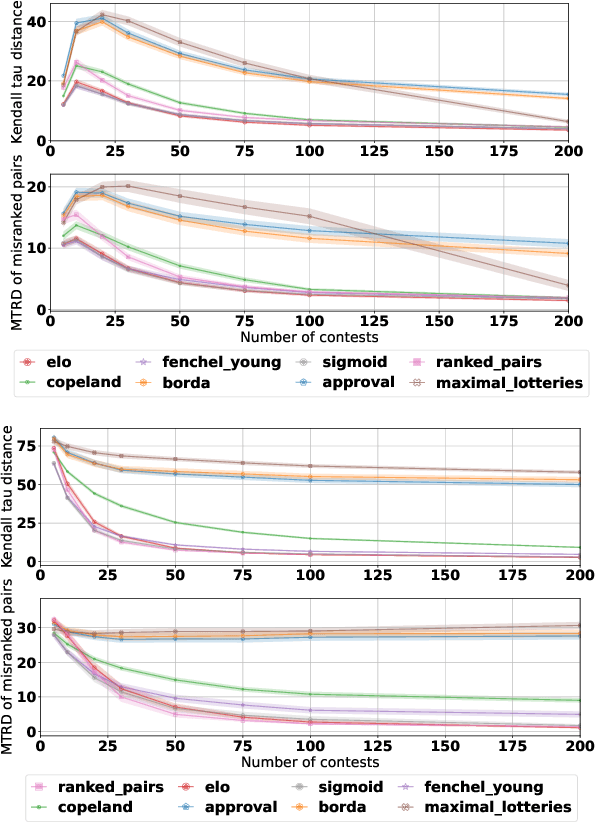
Abstract:A common way to drive progress of AI models and agents is to compare their performance on standardized benchmarks. Comparing the performance of general agents requires aggregating their individual performances across a potentially wide variety of different tasks. In this paper, we describe a novel ranking scheme inspired by social choice frameworks, called Soft Condorcet Optimization (SCO), to compute the optimal ranking of agents: the one that makes the fewest mistakes in predicting the agent comparisons in the evaluation data. This optimal ranking is the maximum likelihood estimate when evaluation data (which we view as votes) are interpreted as noisy samples from a ground truth ranking, a solution to Condorcet's original voting system criteria. SCO ratings are maximal for Condorcet winners when they exist, which we show is not necessarily true for the classical rating system Elo. We propose three optimization algorithms to compute SCO ratings and evaluate their empirical performance. When serving as an approximation to the Kemeny-Young voting method, SCO rankings are on average 0 to 0.043 away from the optimal ranking in normalized Kendall-tau distance across 865 preference profiles from the PrefLib open ranking archive. In a simulated noisy tournament setting, SCO achieves accurate approximations to the ground truth ranking and the best among several baselines when 59\% or more of the preference data is missing. Finally, SCO ranking provides the best approximation to the optimal ranking, measured on held-out test sets, in a problem containing 52,958 human players across 31,049 games of the classic seven-player game of Diplomacy.
Convex Markov Games: A Framework for Fairness, Imitation, and Creativity in Multi-Agent Learning
Oct 22, 2024Abstract:Expert imitation, behavioral diversity, and fairness preferences give rise to preferences in sequential decision making domains that do not decompose additively across time. We introduce the class of convex Markov games that allow general convex preferences over occupancy measures. Despite infinite time horizon and strictly higher generality than Markov games, pure strategy Nash equilibria exist under strict convexity. Furthermore, equilibria can be approximated efficiently by performing gradient descent on an upper bound of exploitability. Our experiments imitate human choices in ultimatum games, reveal novel solutions to the repeated prisoner's dilemma, and find fair solutions in a repeated asymmetric coordination game. In the prisoner's dilemma, our algorithm finds a policy profile that deviates from observed human play only slightly, yet achieves higher per-player utility while also being three orders of magnitude less exploitable.
States as Strings as Strategies: Steering Language Models with Game-Theoretic Solvers
Feb 06, 2024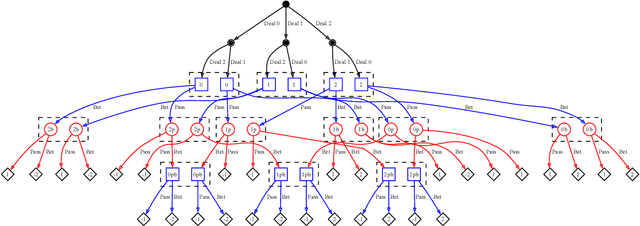

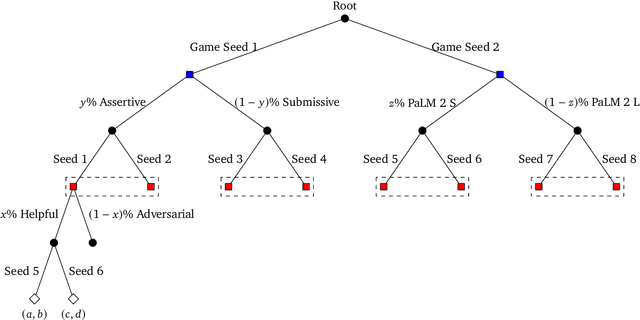
Abstract:Game theory is the study of mathematical models of strategic interactions among rational agents. Language is a key medium of interaction for humans, though it has historically proven difficult to model dialogue and its strategic motivations mathematically. A suitable model of the players, strategies, and payoffs associated with linguistic interactions (i.e., a binding to the conventional symbolic logic of game theory) would enable existing game-theoretic algorithms to provide strategic solutions in the space of language. In other words, a binding could provide a route to computing stable, rational conversational strategies in dialogue. Large language models (LLMs) have arguably reached a point where their generative capabilities can enable realistic, human-like simulations of natural dialogue. By prompting them in various ways, we can steer their responses towards different output utterances. Leveraging the expressivity of natural language, LLMs can also help us quickly generate new dialogue scenarios, which are grounded in real world applications. In this work, we present one possible binding from dialogue to game theory as well as generalizations of existing equilibrium finding algorithms to this setting. In addition, by exploiting LLMs generation capabilities along with our proposed binding, we can synthesize a large repository of formally-defined games in which one can study and test game-theoretic solution concepts. We also demonstrate how one can combine LLM-driven game generation, game-theoretic solvers, and imitation learning to construct a process for improving the strategic capabilities of LLMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge