Paradoxes of Game Theoretic Equilibria and Price of Anarchy

For decades, static solution concepts (Nash, Correlated, and Coarse Correlated Equilibria) and the Price of Anarchy (PoA) have formed the bedrock of algorithmic game theory, with no-regret learning proving fast convergence to such game-theoretic equilibria. We show that reducing multi-agent learning to static equilibrium and black-box regret analysis obscures underlying dynamic disequilibrium and game theoretic bounds. First, interior Nash equilibria lack $C^1$ vector field information, meaning agents cannot distinguish aligned from strictly opposing incentives. Inheriting this geometry, the worst-case pure Nash equilibria dictating robust PoA bounds manifest as topologically unstable strict saddles, and in canonical congestion games, as global repellers supported on almost everywhere strictly dominated strategies. Anchoring efficiency guarantees to these unstable states causes algebraic sensitivity; we prove that accommodating all strictly positive affine costs renders the PoA unbounded. Furthermore, projecting learning trajectories onto the discrete simplex of correlated play systematically accommodates non-rationalizable behavior. Evaluating dynamics via Coarse Correlated Equilibria or proximal refinements fails to preclude strictly dominated strategies. Moreover, optimal $O(1/T)$ swap-regret minimization does not preclude macroscopic turbulence, manifesting as chaotic limit sets even in minimal games. Finally, we examine the non-atomic limit of congestion games. Though considered highly stable with tight sub-linear $Θ(p/\ln p)$ PoA bounds (where $p$ is the polynomial degree), we prove that under discrete-time learning, the unique equilibrium destabilizes into Li-Yorke chaos and global attractors whose time-averaged inefficiency degrades exponentially as $2^p$. These results necessitate re-evaluating worst-case equilibrium frameworks for dynamically grounded metrics.

Deep Incentive Design with Differentiable Equilibrium Blocks

Automated design of multi-agent interactions with desirable equilibrium outcomes is inherently difficult due to the computational hardness, non-uniqueness, and instability of the resulting equilibria. In this work, we propose the use of game-agnostic differentiable equilibrium blocks (DEBs) as modules in a novel, differentiable framework to address a wide variety of incentive design problems from economics and computer science. We call this framework deep incentive design (DID). To validate our approach, we examine three diverse, challenging incentive design tasks: contract design, machine scheduling, and inverse equilibrium problems. For each task, we train a single neural network using a unified pipeline and DEB. This architecture solves the full distribution of problem instances, parameterized by a context, handling all games across a wide range of scales (from two to sixteen actions per player).

Re-evaluating Open-ended Evaluation of Large Language Models

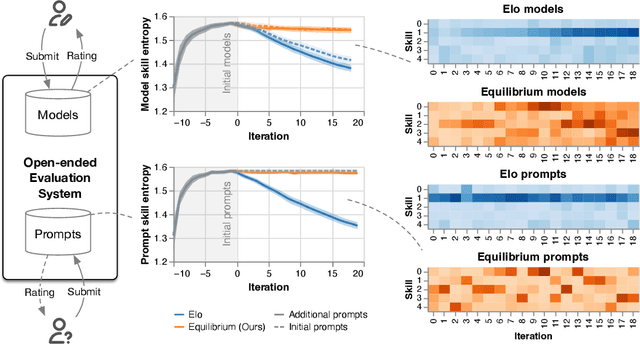
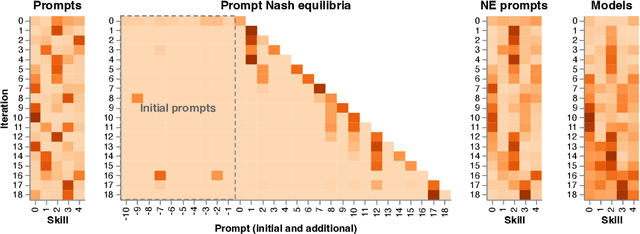
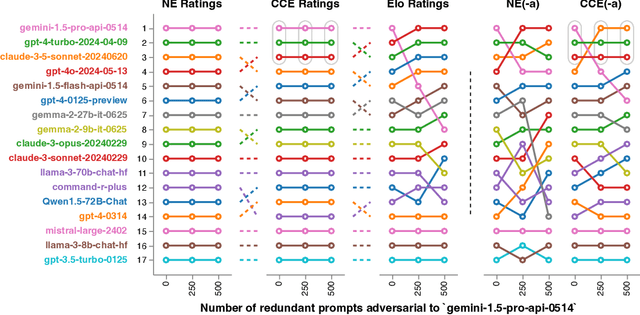
Evaluation has traditionally focused on ranking candidates for a specific skill. Modern generalist models, such as Large Language Models (LLMs), decidedly outpace this paradigm. Open-ended evaluation systems, where candidate models are compared on user-submitted prompts, have emerged as a popular solution. Despite their many advantages, we show that the current Elo-based rating systems can be susceptible to and even reinforce biases in data, intentional or accidental, due to their sensitivity to redundancies. To address this issue, we propose evaluation as a 3-player game, and introduce novel game-theoretic solution concepts to ensure robustness to redundancy. We show that our method leads to intuitive ratings and provide insights into the competitive landscape of LLM development.

Deviation Ratings: A General, Clone-Invariant Rating Method

Many real-world multi-agent or multi-task evaluation scenarios can be naturally modelled as normal-form games due to inherent strategic (adversarial, cooperative, and mixed motive) interactions. These strategic interactions may be agentic (e.g. players trying to win), fundamental (e.g. cost vs quality), or complementary (e.g. niche finding and specialization). In such a formulation, it is the strategies (actions, policies, agents, models, tasks, prompts, etc.) that are rated. However, the rating problem is complicated by redundancy and complexity of N-player strategic interactions. Repeated or similar strategies can distort ratings for those that counter or complement them. Previous work proposed ``clone invariant'' ratings to handle such redundancies, but this was limited to two-player zero-sum (i.e. strictly competitive) interactions. This work introduces the first N-player general-sum clone invariant rating, called deviation ratings, based on coarse correlated equilibria. The rating is explored on several domains including LLMs evaluation.

Convex Markov Games: A Framework for Fairness, Imitation, and Creativity in Multi-Agent Learning

Expert imitation, behavioral diversity, and fairness preferences give rise to preferences in sequential decision making domains that do not decompose additively across time. We introduce the class of convex Markov games that allow general convex preferences over occupancy measures. Despite infinite time horizon and strictly higher generality than Markov games, pure strategy Nash equilibria exist under strict convexity. Furthermore, equilibria can be approximated efficiently by performing gradient descent on an upper bound of exploitability. Our experiments imitate human choices in ultimatum games, reveal novel solutions to the repeated prisoner's dilemma, and find fair solutions in a repeated asymmetric coordination game. In the prisoner's dilemma, our algorithm finds a policy profile that deviates from observed human play only slightly, yet achieves higher per-player utility while also being three orders of magnitude less exploitable.

States as Strings as Strategies: Steering Language Models with Game-Theoretic Solvers

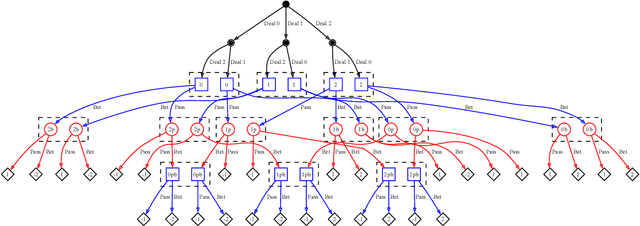
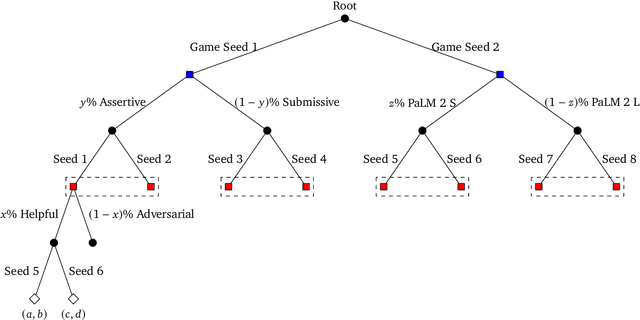
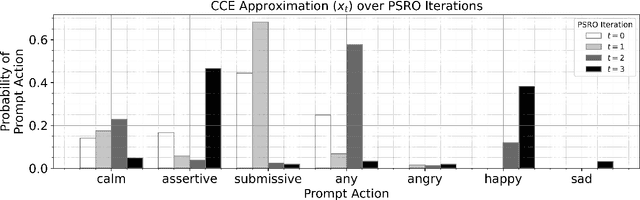
Game theory is the study of mathematical models of strategic interactions among rational agents. Language is a key medium of interaction for humans, though it has historically proven difficult to model dialogue and its strategic motivations mathematically. A suitable model of the players, strategies, and payoffs associated with linguistic interactions (i.e., a binding to the conventional symbolic logic of game theory) would enable existing game-theoretic algorithms to provide strategic solutions in the space of language. In other words, a binding could provide a route to computing stable, rational conversational strategies in dialogue. Large language models (LLMs) have arguably reached a point where their generative capabilities can enable realistic, human-like simulations of natural dialogue. By prompting them in various ways, we can steer their responses towards different output utterances. Leveraging the expressivity of natural language, LLMs can also help us quickly generate new dialogue scenarios, which are grounded in real world applications. In this work, we present one possible binding from dialogue to game theory as well as generalizations of existing equilibrium finding algorithms to this setting. In addition, by exploiting LLMs generation capabilities along with our proposed binding, we can synthesize a large repository of formally-defined games in which one can study and test game-theoretic solution concepts. We also demonstrate how one can combine LLM-driven game generation, game-theoretic solvers, and imitation learning to construct a process for improving the strategic capabilities of LLMs.

Neural Population Learning beyond Symmetric Zero-sum Games

We study computationally efficient methods for finding equilibria in n-player general-sum games, specifically ones that afford complex visuomotor skills. We show how existing methods would struggle in this setting, either computationally or in theory. We then introduce NeuPL-JPSRO, a neural population learning algorithm that benefits from transfer learning of skills and converges to a Coarse Correlated Equilibrium (CCE) of the game. We show empirical convergence in a suite of OpenSpiel games, validated rigorously by exact game solvers. We then deploy NeuPL-JPSRO to complex domains, where our approach enables adaptive coordination in a MuJoCo control domain and skill transfer in capture-the-flag. Our work shows that equilibrium convergent population learning can be implemented at scale and in generality, paving the way towards solving real-world games between heterogeneous players with mixed motives.

Evaluating Agents using Social Choice Theory

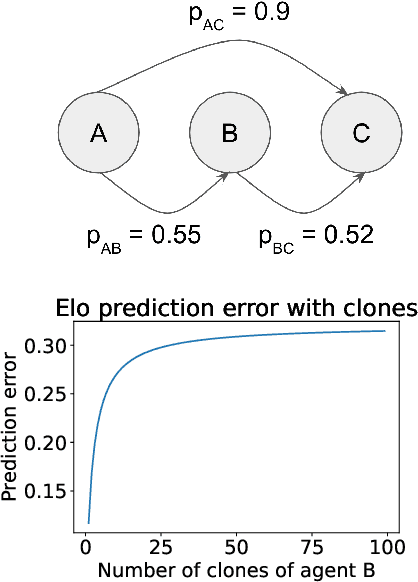
We argue that many general evaluation problems can be viewed through the lens of voting theory. Each task is interpreted as a separate voter, which requires only ordinal rankings or pairwise comparisons of agents to produce an overall evaluation. By viewing the aggregator as a social welfare function, we are able to leverage centuries of research in social choice theory to derive principled evaluation frameworks with axiomatic foundations. These evaluations are interpretable and flexible, while avoiding many of the problems currently facing cross-task evaluation. We apply this Voting-as-Evaluation (VasE) framework across multiple settings, including reinforcement learning, large language models, and humans. In practice, we observe that VasE can be more robust than popular evaluation frameworks (Elo and Nash averaging), discovers properties in the evaluation data not evident from scores alone, and can predict outcomes better than Elo in a complex seven-player game. We identify one particular approach, maximal lotteries, that satisfies important consistency properties relevant to evaluation, is computationally efficient (polynomial in the size of the evaluation data), and identifies game-theoretic cycles.

Combining Tree-Search, Generative Models, and Nash Bargaining Concepts in Game-Theoretic Reinforcement Learning

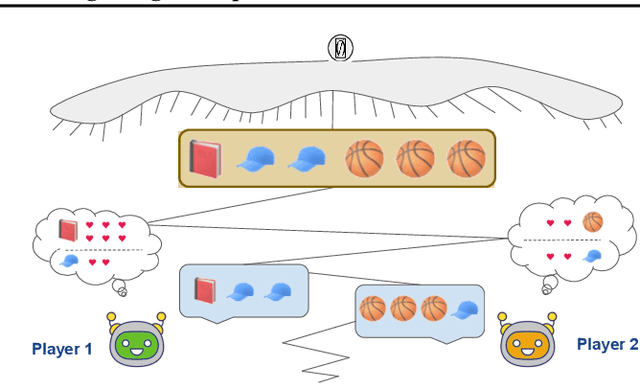
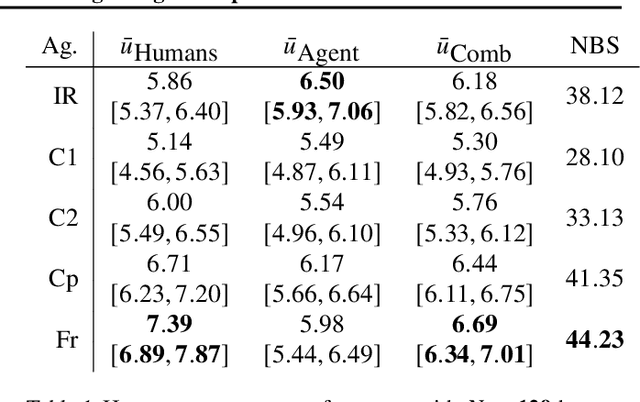
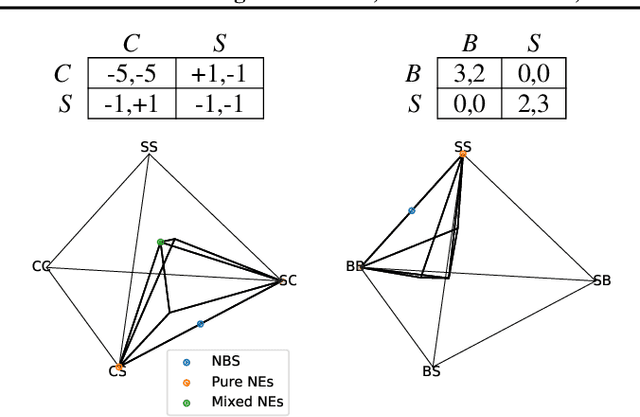
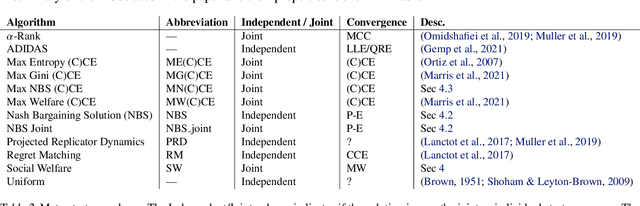
Multiagent reinforcement learning (MARL) has benefited significantly from population-based and game-theoretic training regimes. One approach, Policy-Space Response Oracles (PSRO), employs standard reinforcement learning to compute response policies via approximate best responses and combines them via meta-strategy selection. We augment PSRO by adding a novel search procedure with generative sampling of world states, and introduce two new meta-strategy solvers based on the Nash bargaining solution. We evaluate PSRO's ability to compute approximate Nash equilibrium, and its performance in two negotiation games: Colored Trails, and Deal or No Deal. We conduct behavioral studies where human participants negotiate with our agents ($N = 346$). We find that search with generative modeling finds stronger policies during both training time and test time, enables online Bayesian co-player prediction, and can produce agents that achieve comparable social welfare negotiating with humans as humans trading among themselves.

Turbocharging Solution Concepts: Solving NEs, CEs and CCEs with Neural Equilibrium Solvers

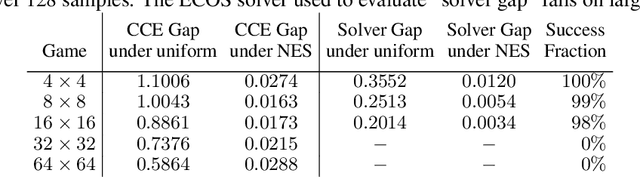
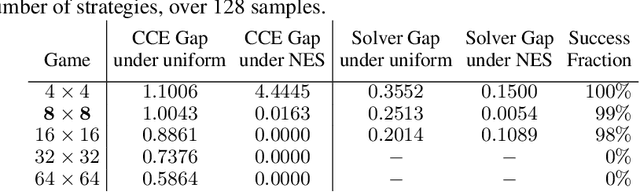
Solution concepts such as Nash Equilibria, Correlated Equilibria, and Coarse Correlated Equilibria are useful components for many multiagent machine learning algorithms. Unfortunately, solving a normal-form game could take prohibitive or non-deterministic time to converge, and could fail. We introduce the Neural Equilibrium Solver which utilizes a special equivariant neural network architecture to approximately solve the space of all games of fixed shape, buying speed and determinism. We define a flexible equilibrium selection framework, that is capable of uniquely selecting an equilibrium that minimizes relative entropy, or maximizes welfare. The network is trained without needing to generate any supervised training data. We show remarkable zero-shot generalization to larger games. We argue that such a network is a powerful component for many possible multiagent algorithms.