Combining Tree-Search, Generative Models, and Nash Bargaining Concepts in Game-Theoretic Reinforcement Learning

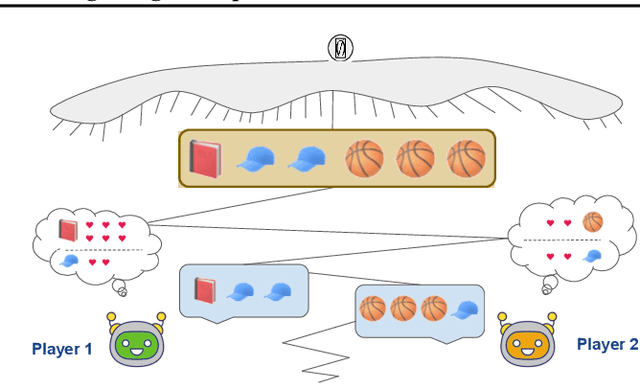
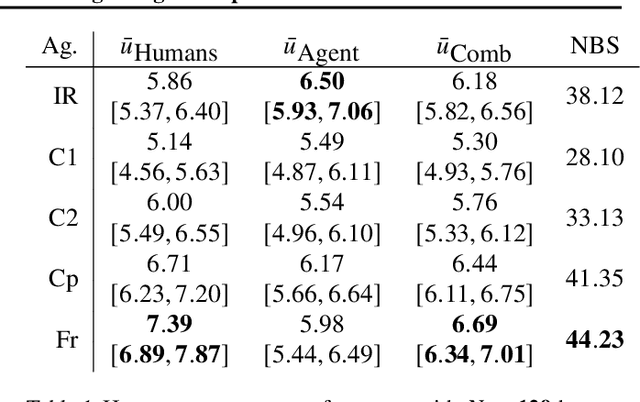
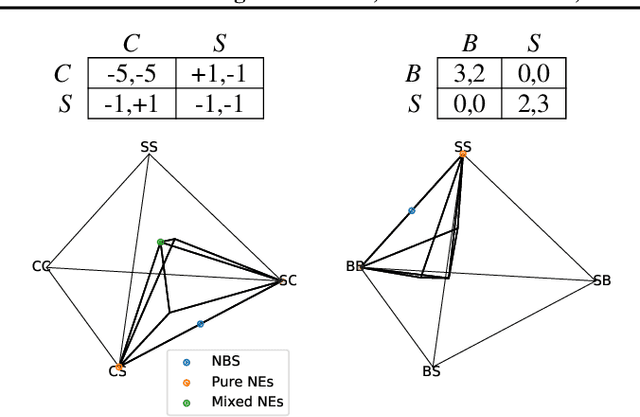
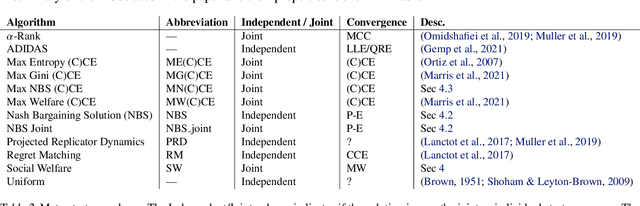
Multiagent reinforcement learning (MARL) has benefited significantly from population-based and game-theoretic training regimes. One approach, Policy-Space Response Oracles (PSRO), employs standard reinforcement learning to compute response policies via approximate best responses and combines them via meta-strategy selection. We augment PSRO by adding a novel search procedure with generative sampling of world states, and introduce two new meta-strategy solvers based on the Nash bargaining solution. We evaluate PSRO's ability to compute approximate Nash equilibrium, and its performance in two negotiation games: Colored Trails, and Deal or No Deal. We conduct behavioral studies where human participants negotiate with our agents ($N = 346$). We find that search with generative modeling finds stronger policies during both training time and test time, enables online Bayesian co-player prediction, and can produce agents that achieve comparable social welfare negotiating with humans as humans trading among themselves.

Developing, Evaluating and Scaling Learning Agents in Multi-Agent Environments

The Game Theory & Multi-Agent team at DeepMind studies several aspects of multi-agent learning ranging from computing approximations to fundamental concepts in game theory to simulating social dilemmas in rich spatial environments and training 3-d humanoids in difficult team coordination tasks. A signature aim of our group is to use the resources and expertise made available to us at DeepMind in deep reinforcement learning to explore multi-agent systems in complex environments and use these benchmarks to advance our understanding. Here, we summarise the recent work of our team and present a taxonomy that we feel highlights many important open challenges in multi-agent research.

Learning Correlated Equilibria in Mean-Field Games

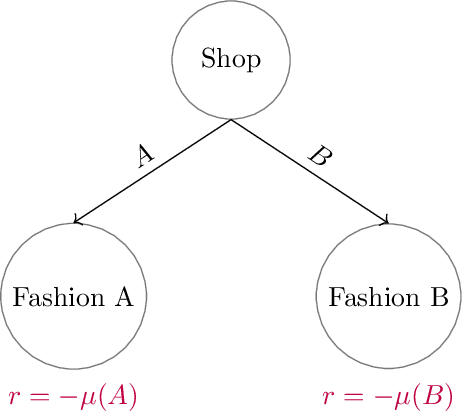
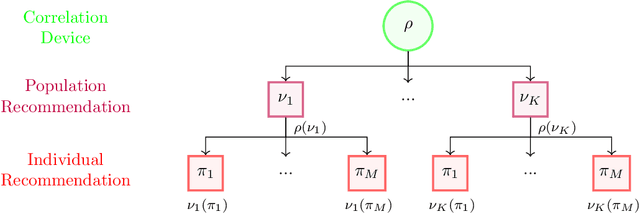
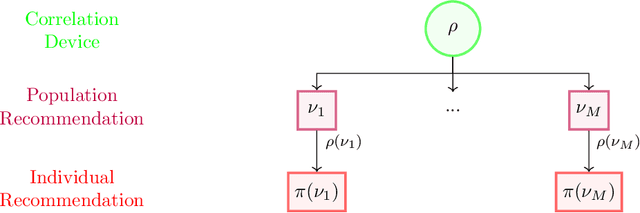
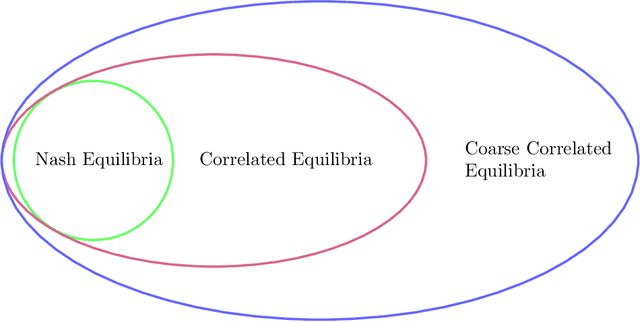
The designs of many large-scale systems today, from traffic routing environments to smart grids, rely on game-theoretic equilibrium concepts. However, as the size of an $N$-player game typically grows exponentially with $N$, standard game theoretic analysis becomes effectively infeasible beyond a low number of players. Recent approaches have gone around this limitation by instead considering Mean-Field games, an approximation of anonymous $N$-player games, where the number of players is infinite and the population's state distribution, instead of every individual player's state, is the object of interest. The practical computability of Mean-Field Nash equilibria, the most studied Mean-Field equilibrium to date, however, typically depends on beneficial non-generic structural properties such as monotonicity or contraction properties, which are required for known algorithms to converge. In this work, we provide an alternative route for studying Mean-Field games, by developing the concepts of Mean-Field correlated and coarse-correlated equilibria. We show that they can be efficiently learnt in \emph{all games}, without requiring any additional assumption on the structure of the game, using three classical algorithms. Furthermore, we establish correspondences between our notions and those already present in the literature, derive optimality bounds for the Mean-Field - $N$-player transition, and empirically demonstrate the convergence of these algorithms on simple games.

Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning

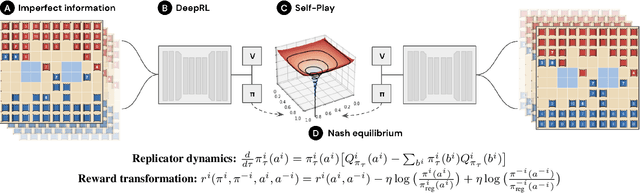
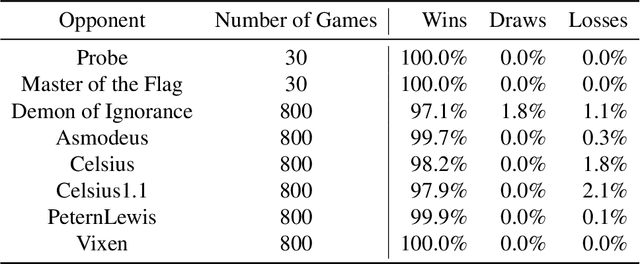
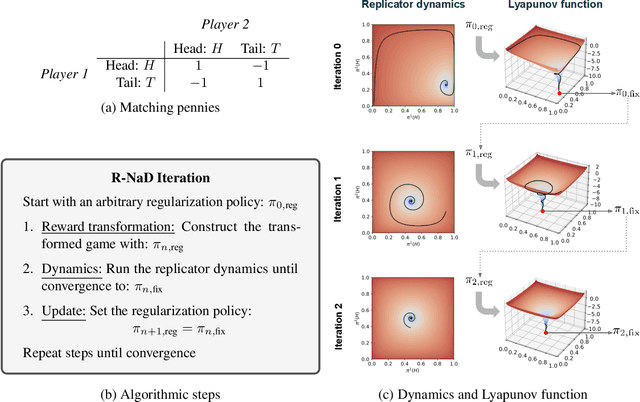
We introduce DeepNash, an autonomous agent capable of learning to play the imperfect information game Stratego from scratch, up to a human expert level. Stratego is one of the few iconic board games that Artificial Intelligence (AI) has not yet mastered. This popular game has an enormous game tree on the order of $10^{535}$ nodes, i.e., $10^{175}$ times larger than that of Go. It has the additional complexity of requiring decision-making under imperfect information, similar to Texas hold'em poker, which has a significantly smaller game tree (on the order of $10^{164}$ nodes). Decisions in Stratego are made over a large number of discrete actions with no obvious link between action and outcome. Episodes are long, with often hundreds of moves before a player wins, and situations in Stratego can not easily be broken down into manageably-sized sub-problems as in poker. For these reasons, Stratego has been a grand challenge for the field of AI for decades, and existing AI methods barely reach an amateur level of play. DeepNash uses a game-theoretic, model-free deep reinforcement learning method, without search, that learns to master Stratego via self-play. The Regularised Nash Dynamics (R-NaD) algorithm, a key component of DeepNash, converges to an approximate Nash equilibrium, instead of 'cycling' around it, by directly modifying the underlying multi-agent learning dynamics. DeepNash beats existing state-of-the-art AI methods in Stratego and achieved a yearly (2022) and all-time top-3 rank on the Gravon games platform, competing with human expert players.

Scalable Deep Reinforcement Learning Algorithms for Mean Field Games

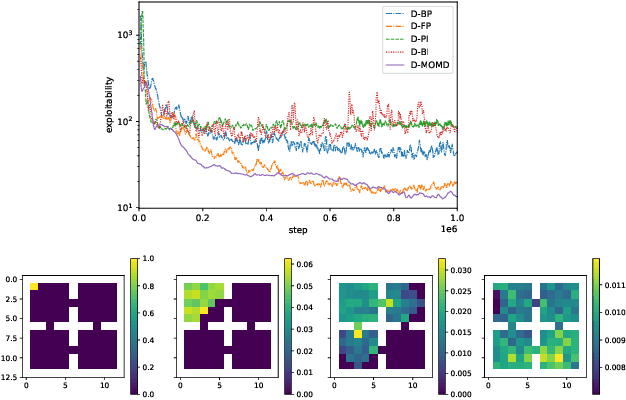
Mean Field Games (MFGs) have been introduced to efficiently approximate games with very large populations of strategic agents. Recently, the question of learning equilibria in MFGs has gained momentum, particularly using model-free reinforcement learning (RL) methods. One limiting factor to further scale up using RL is that existing algorithms to solve MFGs require the mixing of approximated quantities such as strategies or $q$-values. This is non-trivial in the case of non-linear function approximation that enjoy good generalization properties, e.g. neural networks. We propose two methods to address this shortcoming. The first one learns a mixed strategy from distillation of historical data into a neural network and is applied to the Fictitious Play algorithm. The second one is an online mixing method based on regularization that does not require memorizing historical data or previous estimates. It is used to extend Online Mirror Descent. We demonstrate numerically that these methods efficiently enable the use of Deep RL algorithms to solve various MFGs. In addition, we show that these methods outperform SotA baselines from the literature.

Multi-Agent Training beyond Zero-Sum with Correlated Equilibrium Meta-Solvers

Two-player, constant-sum games are well studied in the literature, but there has been limited progress outside of this setting. We propose Joint Policy-Space Response Oracles (JPSRO), an algorithm for training agents in n-player, general-sum extensive form games, which provably converges to an equilibrium. We further suggest correlated equilibria (CE) as promising meta-solvers, and propose a novel solution concept Maximum Gini Correlated Equilibrium (MGCE), a principled and computationally efficient family of solutions for solving the correlated equilibrium selection problem. We conduct several experiments using CE meta-solvers for JPSRO and demonstrate convergence on n-player, general-sum games.

Time-series Imputation of Temporally-occluded Multiagent Trajectories

In multiagent environments, several decision-making individuals interact while adhering to the dynamics constraints imposed by the environment. These interactions, combined with the potential stochasticity of the agents' decision-making processes, make such systems complex and interesting to study from a dynamical perspective. Significant research has been conducted on learning models for forward-direction estimation of agent behaviors, for example, pedestrian predictions used for collision-avoidance in self-driving cars. However, in many settings, only sporadic observations of agents may be available in a given trajectory sequence. For instance, in football, subsets of players may come in and out of view of broadcast video footage, while unobserved players continue to interact off-screen. In this paper, we study the problem of multiagent time-series imputation, where available past and future observations of subsets of agents are used to estimate missing observations for other agents. Our approach, called the Graph Imputer, uses forward- and backward-information in combination with graph networks and variational autoencoders to enable learning of a distribution of imputed trajectories. We evaluate our approach on a dataset of football matches, using a projective camera module to train and evaluate our model for the off-screen player state estimation setting. We illustrate that our method outperforms several state-of-the-art approaches, including those hand-crafted for football.

From Motor Control to Team Play in Simulated Humanoid Football

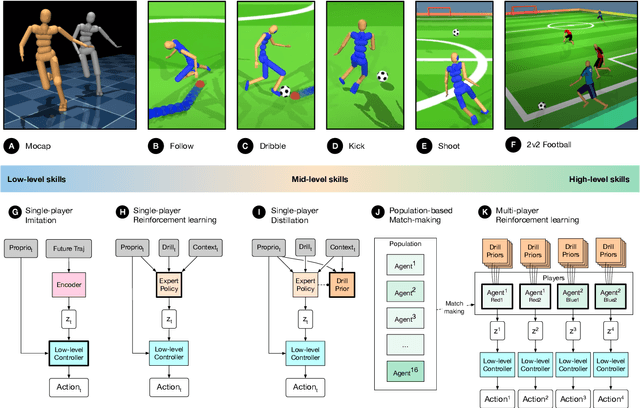
Intelligent behaviour in the physical world exhibits structure at multiple spatial and temporal scales. Although movements are ultimately executed at the level of instantaneous muscle tensions or joint torques, they must be selected to serve goals defined on much longer timescales, and in terms of relations that extend far beyond the body itself, ultimately involving coordination with other agents. Recent research in artificial intelligence has shown the promise of learning-based approaches to the respective problems of complex movement, longer-term planning and multi-agent coordination. However, there is limited research aimed at their integration. We study this problem by training teams of physically simulated humanoid avatars to play football in a realistic virtual environment. We develop a method that combines imitation learning, single- and multi-agent reinforcement learning and population-based training, and makes use of transferable representations of behaviour for decision making at different levels of abstraction. In a sequence of stages, players first learn to control a fully articulated body to perform realistic, human-like movements such as running and turning; they then acquire mid-level football skills such as dribbling and shooting; finally, they develop awareness of others and play as a team, bridging the gap between low-level motor control at a timescale of milliseconds, and coordinated goal-directed behaviour as a team at the timescale of tens of seconds. We investigate the emergence of behaviours at different levels of abstraction, as well as the representations that underlie these behaviours using several analysis techniques, including statistics from real-world sports analytics. Our work constitutes a complete demonstration of integrated decision-making at multiple scales in a physically embodied multi-agent setting. See project video at https://youtu.be/KHMwq9pv7mg.

Game Plan: What AI can do for Football, and What Football can do for AI

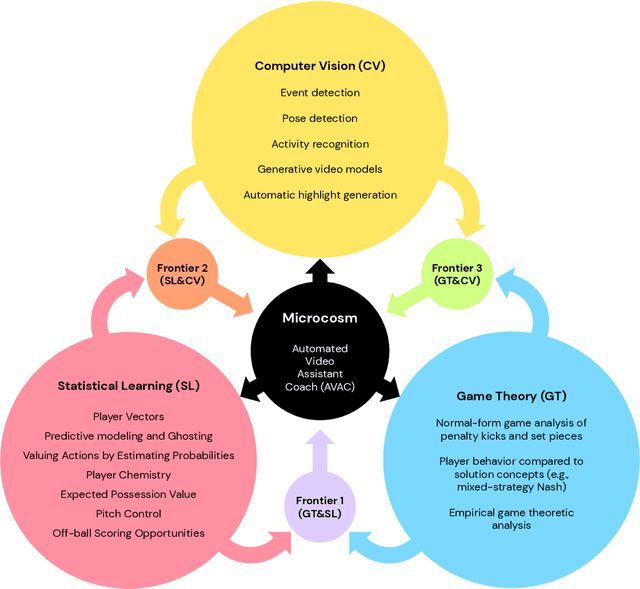
The rapid progress in artificial intelligence (AI) and machine learning has opened unprecedented analytics possibilities in various team and individual sports, including baseball, basketball, and tennis. More recently, AI techniques have been applied to football, due to a huge increase in data collection by professional teams, increased computational power, and advances in machine learning, with the goal of better addressing new scientific challenges involved in the analysis of both individual players' and coordinated teams' behaviors. The research challenges associated with predictive and prescriptive football analytics require new developments and progress at the intersection of statistical learning, game theory, and computer vision. In this paper, we provide an overarching perspective highlighting how the combination of these fields, in particular, forms a unique microcosm for AI research, while offering mutual benefits for professional teams, spectators, and broadcasters in the years to come. We illustrate that this duality makes football analytics a game changer of tremendous value, in terms of not only changing the game of football itself, but also in terms of what this domain can mean for the field of AI. We review the state-of-the-art and exemplify the types of analysis enabled by combining the aforementioned fields, including illustrative examples of counterfactual analysis using predictive models, and the combination of game-theoretic analysis of penalty kicks with statistical learning of player attributes. We conclude by highlighting envisioned downstream impacts, including possibilities for extensions to other sports (real and virtual).

Navigating the Landscape of Games

Games are traditionally recognized as one of the key testbeds underlying progress in artificial intelligence (AI), aptly referred to as the "Drosophila of AI". Traditionally, researchers have focused on using games to build strong AI agents that, e.g., achieve human-level performance. This progress, however, also requires a classification of how 'interesting' a game is for an artificial agent. Tackling this latter question not only facilitates an understanding of the characteristics of learnt AI agents in games, but also helps to determine what game an AI should address next as part of its training. Here, we show how network measures applied to so-called response graphs of large-scale games enable the creation of a useful landscape of games, quantifying the relationships between games of widely varying sizes, characteristics, and complexities. We illustrate our findings in various domains, ranging from well-studied canonical games to significantly more complex empirical games capturing the performance of trained AI agents pitted against one another. Our results culminate in a demonstration of how one can leverage this information to automatically generate new and interesting games, including mixtures of empirical games synthesized from real world games.