Scalable Deep Reinforcement Learning Algorithms for Mean Field Games

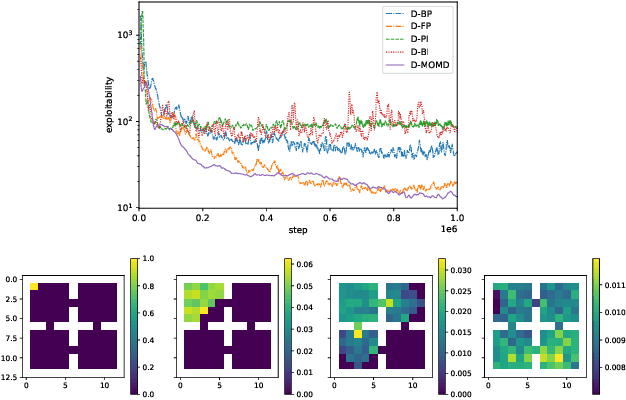
Mean Field Games (MFGs) have been introduced to efficiently approximate games with very large populations of strategic agents. Recently, the question of learning equilibria in MFGs has gained momentum, particularly using model-free reinforcement learning (RL) methods. One limiting factor to further scale up using RL is that existing algorithms to solve MFGs require the mixing of approximated quantities such as strategies or $q$-values. This is non-trivial in the case of non-linear function approximation that enjoy good generalization properties, e.g. neural networks. We propose two methods to address this shortcoming. The first one learns a mixed strategy from distillation of historical data into a neural network and is applied to the Fictitious Play algorithm. The second one is an online mixing method based on regularization that does not require memorizing historical data or previous estimates. It is used to extend Online Mirror Descent. We demonstrate numerically that these methods efficiently enable the use of Deep RL algorithms to solve various MFGs. In addition, we show that these methods outperform SotA baselines from the literature.

Generalization in Mean Field Games by Learning Master Policies

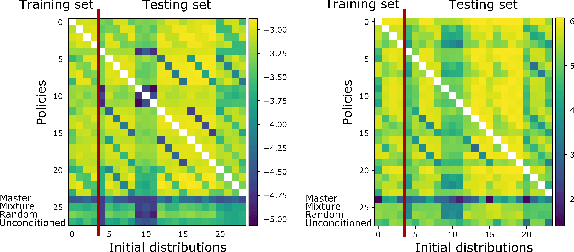
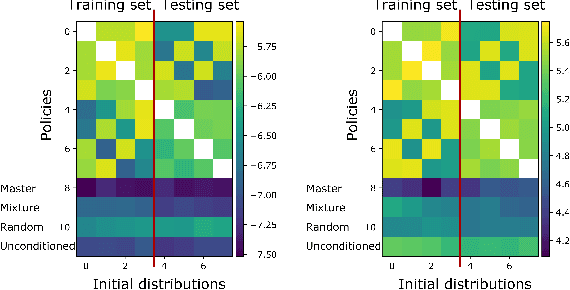
Mean Field Games (MFGs) can potentially scale multi-agent systems to extremely large populations of agents. Yet, most of the literature assumes a single initial distribution for the agents, which limits the practical applications of MFGs. Machine Learning has the potential to solve a wider diversity of MFG problems thanks to generalizations capacities. We study how to leverage these generalization properties to learn policies enabling a typical agent to behave optimally against any population distribution. In reference to the Master equation in MFGs, we coin the term ``Master policies'' to describe them and we prove that a single Master policy provides a Nash equilibrium, whatever the initial distribution. We propose a method to learn such Master policies. Our approach relies on three ingredients: adding the current population distribution as part of the observation, approximating Master policies with neural networks, and training via Reinforcement Learning and Fictitious Play. We illustrate on numerical examples not only the efficiency of the learned Master policy but also its generalization capabilities beyond the distributions used for training.

Mean Field Games Flock! The Reinforcement Learning Way

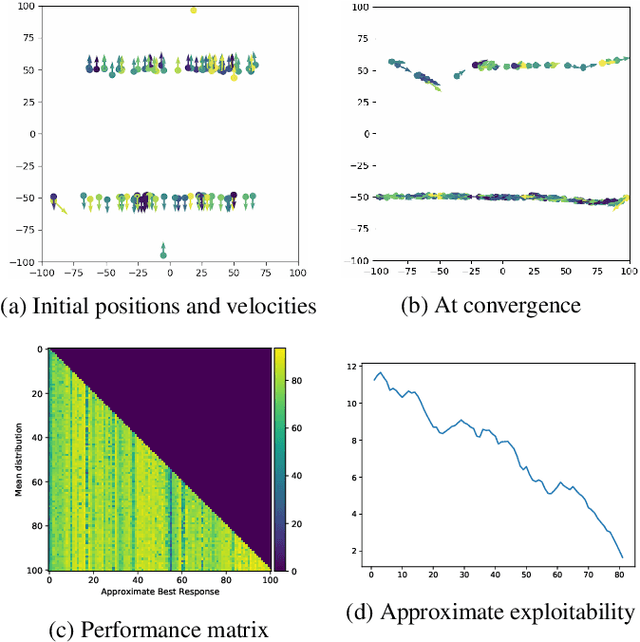
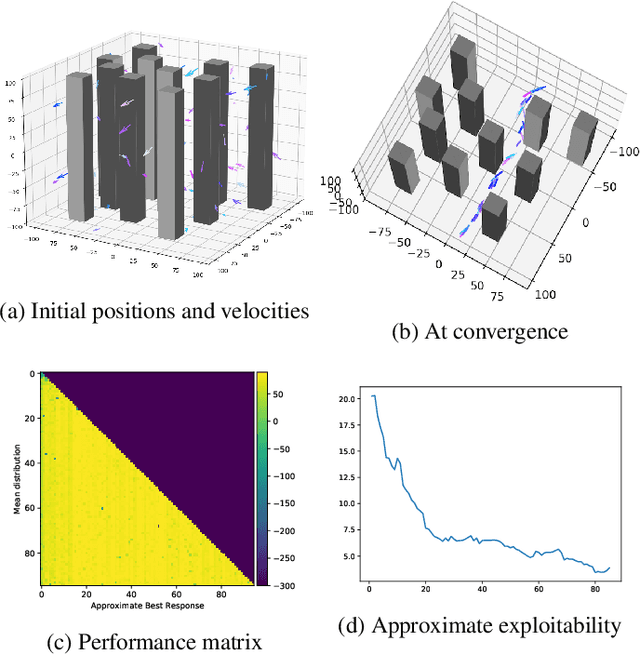
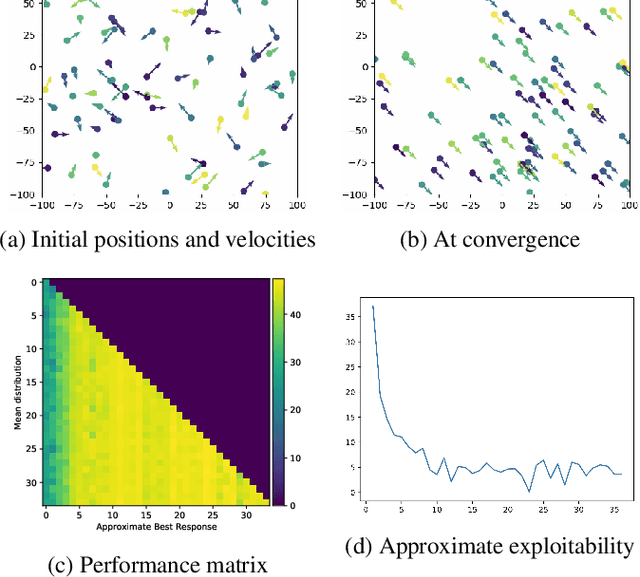
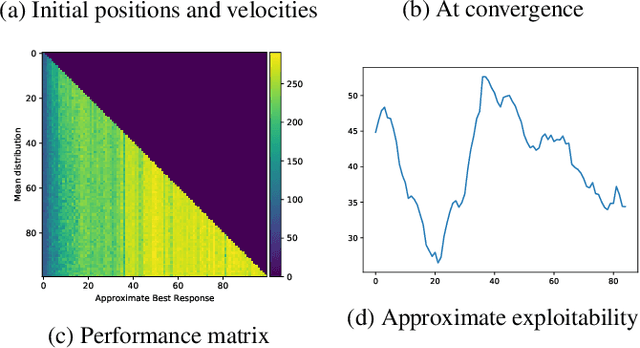
We present a method enabling a large number of agents to learn how to flock, which is a natural behavior observed in large populations of animals. This problem has drawn a lot of interest but requires many structural assumptions and is tractable only in small dimensions. We phrase this problem as a Mean Field Game (MFG), where each individual chooses its acceleration depending on the population behavior. Combining Deep Reinforcement Learning (RL) and Normalizing Flows (NF), we obtain a tractable solution requiring only very weak assumptions. Our algorithm finds a Nash Equilibrium and the agents adapt their velocity to match the neighboring flock's average one. We use Fictitious Play and alternate: (1) computing an approximate best response with Deep RL, and (2) estimating the next population distribution with NF. We show numerically that our algorithm learn multi-group or high-dimensional flocking with obstacles.